部分歪対称関数の歪対称化、少し短く - 檜山正幸のキマイラ飼育記 (はてなBlog)

12月29日に書いた「部分歪対称関数の歪対称化」ですが、準備と計算が矢鱈に長ったらしくて、なんかショートカットがあるんじゃないか？という感じがしていました。年をまたぐ前にケリを付けたい。

本質的には同じことをするのですが、幾分かは短く出来ることが分かりました。置換の分解と符号〈偶奇性 | パリティ〉の簡単な性質だけから結果が出ます。使う用語・記法は「部分歪対称関数の歪対称化」と同じです。

最終的な形が少し変わります（言ってる内容は同じです）。

関数 $f: X^{![0, p]} \to R$ が、 $[1, p]$ に関して部分歪対称ならば、次の等式が成立する。

$\mbox{For }\pmb{x} \in X^{![0, p]} \\ {\displaystyle \sum_{ \rho \in S([0, p]) } f(\pmb{x}\cdot \rho) = p!\left( f(\pmb{x}) - \sum_{j = 1}^p f( \pmb{x}\cdot \tau(0, j) ) \right) }$

内容：

置換の分解、別な方法
歪対称化作用素の計算

置換の分解、別な方法

$S([0, p]) \cong [0, p]\times S([1, p])$ という同型はどうも必要そうです。次のような1:1対応があるわけです。

$\mbox{For } \rho \in S([0, p]), j\in [0, p], \sigma\in S([1, p]) \\ \:\:\:\: \rho \leftrightarrow (j, \sigma)$

「部分歪対称関数の歪対称化」では、上記の1:1対応を作るためにバブルアップ置換を使いました。今回はバブルアップ置換ではなくて、互換〈transposition〉を使います。i, j∈[0, p] に対して、i と j を入れ替える置換を互換と呼び τ(i, j) と書くことにします。

埋め込み emb:S([1, p]) → S([0, p]) は「部分歪対称関数の歪対称化」で述べたとおりです（自然な埋め込み）。置換の組み合わせ構成〈combination〉comb:[0, p] × S([1, p]) → S([0, p]) の定義を次のように変更します。

$\mbox{For }j\in [0, p], \sigma\in S([0, p])\\ \:\:\:\: comb(j, \sigma) = j\triangle \sigma := \tau(0, j)\circ emb(\sigma)$

$\rho = comb(j, \sigma) = j\triangle \sigma$ として絵を描くと次のようになります。

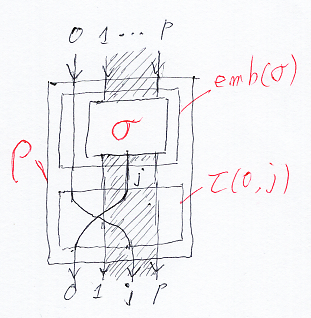
場合分けをプログラム風にキチンと書いてみます。関数〈写像〉の記述にラムダ記法を使っていて、/* ‥‥ */ はコメントです。

$[0, p]\times S([1, p]) \ni (j, \sigma) \mapsto \rho \in S([0, p])$

if (j = 0) then
  ρ := emb(σ)
else /* 1 ≦ j ≦ p */
  ρ := λi∈[0, p].(
    if (i = 0) then
      j  /* 1 ≦ ρ(i) = j ≦ p */
    elseif (σ(i) = j) then
      0 /* ρ(i) = 0 */
    else
      σ(i) /* ρ(i) = σ(i) */
    endif
  )
endif

逆向きの対応は次のように書けます。

$S([0, p]) \ni \rho \mapsto (j, \sigma) \in [0, p]\times S([1, p])$

j := ρ(0)

if (j = 0) then
  σ := λi∈[1, p].ρ(i) /* σ は ρ の [1, p] への制限 */
else         
  σ := λi∈[1, p].(
    if (ρ(i) = 0) then
      j /* σ(i) = j */
    else /* ρ(i) ≠ 0 のとき */
      ρ(i) /* σ(i) = ρ(i) */
    endif
  )
endif

このように定義した同型 $S([0, p]) \cong [0, p]\times S([1, p])$ により、S([0, p]) 上の総和は、[0, p] × S([1, p]) 上の総和に置き換え可能です。

念の為、互換の符号について言っておくと：

$\mbox{if } (j = 0) \mbox{ then }\\ \:\:\:\: sign(\tau(0, j)) = sign(\tau(0, 0)) = 1 \\ \mbox{if } (j \ne 0) \mbox{ then }\\ \:\:\:\: sign(\tau(0, j)) = -1$

この事実から、次の形の等式が出てきます。

$\:\:\:\:{\displaystyle \sum_{j = 0}^p sign(\tau(0, j))\,\psi_j }\\ = {\displaystyle \psi_0 - \sum_{j = 1}^p \psi_j }$

歪対称化作用素の計算

関数 f:X^{![0, p]} → R は、先頭（0番目）を除く残りの変数に関しては歪対称だとします。次の総和を計算します。

${\displaystyle \sum_{\rho \in S([0, 1])}f(\pmb{x}\cdot \rho) sign(\rho) }$

置換の分解 ρ ←→ (j, σ) により、次のように書き換えられます。ここは前回と同じですが、 $j\triangle \sigma$ の定義は変更されています。

${\displaystyle \sum_{\rho \in S([0, 1])}f(\pmb{x}\cdot \rho) sign(\rho) } \\ = {\displaystyle \sum_{ (j, \sigma) \in [0, 1]\times S([1, p])} f(\pmb{x}\cdot (j\triangle\sigma) ) sign(j \triangle\sigma) } \\ = {\displaystyle \sum_{j = 0}^p \sum_{ \sigma\in S([1, p]) } f(\pmb{x}\cdot (j\triangle\sigma) ) sign(j \triangle\sigma) }$

総和される $f(\pmb{x}\cdot (j\triangle\sigma) ) sign(j \triangle\sigma)$ を、 $j\triangle \sigma = comb(j, \sigma)$ の定義に従い書き換えます。

$\:\:\:\: f(\pmb{x}\cdot (j\triangle\sigma) ) sign(j \triangle\sigma) \\ = f(\pmb{x}\cdot (\tau(0, j) \circ emb(\sigma) ) ) sign(\tau(0, j)\circ emb(\sigma) ) \\ = f( ( \pmb{x}\cdot \tau(0, j) ) \cdot emb(\sigma) ) sign(\tau(0, j))sign( emb(\sigma) ) \\ = sign(\tau(0, j)) f( (\pmb{x}\cdot \tau(0, j) ) \cdot emb(\sigma) ) sign(\sigma )$

$( \pmb{x}\cdot \tau(0, j) ) =: \pmb{t}$ と置けば：

$\:\:\:\: f( (\pmb{x}\cdot \tau(0, j) ) \cdot emb(\sigma) ) sign(\sigma ) \\ = f( \pmb{t} \cdot emb(\sigma) ) sign(\sigma )$

長さが(p + 1)のタプル $\pmb{t}$ に emb(σ) を作用させるとは、 $\pmb{t}$ の先頭を除いた部分（rest部分）に σ を作用させることと同じであることに注意してください。

j は固定した状態で、σ∈S([1, p]) に渡って総和をとります。

$\:\:\:\: {\displaystyle\sum_{\sigma\in S([1,p])} f(\pmb{x}\cdot (j\triangle\sigma) ) sign(j \triangle\sigma) }\\ = {\displaystyle \sum_{\sigma\in S([1,p])} sign(\tau(0, j)) f( (\pmb{x}\cdot \tau(0, j) ) \cdot emb(\sigma) ) sign(\sigma ) }\\ = p!\, sign(\tau(0, j)) f(\pmb{x}\cdot \tau(0, j) )$

ここで、fの部分歪対称性の仮定を使っています。

これを j = 0, 1, ..., p に渡って総和します。

$\:\:\:\: {\displaystyle \sum_{j = 0}^p p!\, sign(\tau(0, j)) f(\pmb{x}\cdot \tau(0, j) ) }\\ = {\displaystyle p! \left( sign(\tau(0, 0)) f(\pmb{x}\cdot \tau(0, 0) ) + \sum_{j = 1}^p sign(\tau(0, j)) f(\pmb{x}\cdot \tau(0, j) ) \right) }\\ = {\displaystyle p! \left( f(\pmb{x} ) - \sum_{j = 1}^p f(\pmb{x}\cdot \tau(0, j) ) \right) }$

これで求めていた結果が得られました。よいお年をお迎えください。