ストリング図を描く際に、ボックス〈ノード〉は基本的かつ重要な描画要素です。絵に描いたボックスに対応する組み合わせ構造はいったい何なのでしょう? ボックスは、色付きコレクションの視覚化なのだとみなすのが良さそうです。なので、この記事では色付きコレクションについて述べます。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\pipe}{\mid }
\newcommand{\ccol}[1]{\boldsymbol{#1} }
%\newcommand{\msf}[1]{\mathsf{#1}}
\newcommand{\twoto}{\Rightarrow }
\newcommand{\In}{\text{ in } }
%\newcommand{\Imp}{ \Rightarrow }
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\hyp}{\text{-} }
\newcommand{\op}{\mathrm{op} }
%\newcommand{\id}{\mathrm{id} }
%\newcommand{\pto}{ \supseteq\!\to }
\newcommand{\u}[1]{\underline{#1}}
\newcommand{\cpal}[1]{\mathfrak{#1} }
%\newcommand{\msc}[1]{\mathscr{#1}}
`$
内容:
準備
2つの自然数 $`n, m\in {\bf N}`$ に対して、次のような(ドット2個の)記法を約束します。
$`\quad n..m := \{k\in {\bf N}\mid n \le k \land k \le m\}`$
$`n \gt m`$ のときは、$`n..m`$ は空集合です。空集合になっても別にかまいませんが、主に $`n \le m`$ である場合に $`n..m`$ を使います。特によく使うケースのためにさらに次の約束をします。
$`\quad \bar{n} := 1..n`$
$`\bar{0}`$ は空集合です。
圏 $`\cat{C}`$ の対象 $`X`$ の自己同型射の群を $`\mrm{Aut}_\cat{C}(X)`$ と書きます。下付きの $`\cat{C}`$ を省略した場合のデフォルトは集合圏だとします。つまり:
$`\quad \mrm{Aut}(X) := \mrm{Aut}_{\bf Set}(X) \; \in |{\bf Grp}|`$ ($`{\bf Grp}`$ は群の圏)
$`\mrm{Aut}(\bar{n})`$ は$`n`$次の対称群〈the symmetric group of degree $`n`$〉です。
圏 $`\cat{C}`$ の対象 $`X, Y`$ のあいだの同型射の集合を $`\mrm{Iso}_\cat{C}(X, Y)`$ と書きます。下付きの $`\cat{C}`$ を省略した場合のデフォルトは集合圏だとします。つまり:
$`\quad \mrm{Iso}(X, Y) := \mrm{Iso}_{\bf Set}(X, Y) \; \in |{\bf Set}|`$
射の結合〈composition〉を図式順に書いた場合、集合 $`\mrm{Iso}(X, Y)`$ は、左から $`\mrm{Aut}(X)`$ による群作用、右から $`\mrm{Aut}(Y)`$ による群作用を持ちます。例えば、$`\mrm{Iso}(X, \bar{n})`$ は、$`n`$次対称群による右群作用を持ちます。結合の書き方が反図式順なら、左作用とみなすほうが(書き方の観点からは)自然です。
集合圏のホムセット $`{\bf Set}(X, Y)`$ は $`\mrm{Map}(X, Y)`$ とも書きます。例えば、長さが $`n`$ で項目の型が $`X`$ であるリストの集合は $`\mrm{Map}(\bar{n}, X)`$ です。$`\mrm{Map}(\bar{0}, X)`$ は単元集合で、唯一の要素は空リストです。
コレクション
コレクションは、次のようなモノの“集まり”の総称です。
- 単なる有限集合
- 有限な全順序集合
- 有限なサイクリック順序集合(順序集合の一種ではない)
様々なコレクションを一様に扱うために、コレクションは台集合と(許容される)列挙〈enumeration〉の集合の組として定義します。
コレクション〈collection〉 $`X`$ は次の構成素からなります。
- 有限集合 $`\u{X}`$ (台集合)
- 自然数 $`n`$
- 許容される列挙の集合 $`\mrm{Enum}(X) \subseteq \mrm{Iso}(\u{X}, \bar{n})`$
これは次の条件(コレクションの公理)を満たします。
- $`\mrm{Enum}(X)`$ は空ではない。
- $`e_1, e_2, e_3\in \mrm{Enum}(X)`$ ならば、$`e_1;{e_2}^{-1};e_3 \in \mrm{Enum}(X)`$
$`\mrm{Enum}(X)`$ の要素を、コレクション $`X`$ の列挙〈enumeration〉と呼びます。$`\mrm{Enum}(X)`$ は空ではないので、$`e\in \mrm{Enum}(X)`$ である $`e`$ (列挙)が存在します。それは $`e\in \mrm{Iso}(\u{X}, \bar{n})`$ です。したがって、自然数 $`n`$ は有限集合 $`\u{X}`$ の基数〈cardinality〉です。
$`e_1, e_2\in \mrm{Enum}(X)`$ により $`{e_1}^{-1}; e_2`$ と書ける $`\mrm{Aut}(\bar{n})`$ の要素達は、$`n`$次対称群の部分群になります(コレクションの条件から言える)。この部分群を $`\mrm{Sym}(X) \subseteq \mrm{Aut}(\bar{n})`$ と書き、コレクション $`X`$ の対称性群〈symmetry group〉と呼びます。対称群と対称性群は違うので注意してください。
ひとつの列挙 $`e: \u{X} \to \bar{n} \In {\bf FinSet}`$ と、対称性群 $`\mrm{Sym}(X)`$ から、$`X`$ の列挙の集合 $`\mrm{Enum}(X)`$ は再現できます。これを利用して、コレクションを定義する際に、次のモノ達を指定してもかまいません。
- 有限集合 $`\u{X}`$
- 自然数 $`n`$
- 同型写像 $`e: \u{X} \to \bar{n} \In {\bf FinSet}`$
- $`n`$次対称群の部分群 $`G \subseteq \mrm{Aut}(\bar{n})`$
集合として $`\mrm{Enum}(X) \cong \mrm{Sym}(X)`$ ですが、規準的な〈canonical〉同型はありません。離散有限ですが、$`\mrm{Enum}(X)`$ は群の“等質空間”だと言えます。
すべてのコレクション達は圏を形成しますが、このとき、コレクションのあいだの同型射だけを考えることにします。後で必要なのは同型射だけだからです。
$`X, Y`$ をコレクションとして、台集合のあいだの同型射〈双射 | 全単射〉 $`f: \u{X} \to \u{Y} \In {\bf FinSet}`$ が、列挙の集合のあいだの同型を誘導するときに、コレクションのあいだの同型射〈isomorphism〉と呼びます。これは次の写像の像がちょうど $`\mrm{Enum}(X)`$ になることです。
$`\quad \mrm{Enum}(Y) \ni e \mapsto f;e \in \mrm{Iso}(X, \bar{n})`$
台写像 $`f`$ が誘導する列挙の集合のあいだの同型を $`f^*`$ と(略記として)書きます。
$`\quad f^* : \mrm{Enum}(Y) \overset{\cong}{\to} \mrm{Enum}(X) \In {\bf FinSet}`$
すべてのコレクションを対象類〈class of objects〉として、コレクションのあいだの同型射を射とする圏を $`{\bf CollG}`$ とします。末尾の'G'は groupoid〈亜群〉のつもりです。
亜群 $`{\bf CollG}`$ をそのまま使うことはあまりなくて、部分亜群を使います(次節で説明)。
典型的なコレクション亜群
コレクションの定義から、どんなコレクションにも少なくとも1つの列挙があります。列挙を1つだけ備えたコレクション達からなる $`{\bf CollG}`$ の部分亜群を $`{\bf OrdCollG}`$ とします。部分亜群 $`{\bf OrdCollG}`$ の対象を順序付きコレクション〈ordered collection | 順序コレクション〉と呼びます。
有限な全順序集合〈finite totally ordered set〉を対象として、順序を保存する写像〈単調写像〉を射とする圏を $`{\bf FinTotOrd}`$ とします。次のような圏の同型(同値より強い)があります。
$`\quad {\bf OrdCollG} \cong \mrm{Core}({\bf FinTotOrd}) \In {\bf CAT}`$
$`\mrm{Core}(\hyp)`$ は、圏のコア亜群〈core groupoid〉です。
唯一の列挙 $`e:\u{X} \to \bar{n} \In {\bf FinSet}`$ を持つコレクションは、$`1 \lt \cdots \lt n`$ の順序を $`\u{X}`$ 上に持ち込めば全順序集合になります。この方法で、列挙を1つだけ備えたコレクションと有限全順序集合を同一視できます。
別なコレクションの種別として $`\mrm{Enum}(X) = \mrm{Iso}(\u{X}, \bar{n})`$ であるコレクションがあります。この種のコレクション達を対象類とする $`{\bf CollG}`$ の部分亜群を $`{\bf UnoCollG}`$ とします。部分亜群 $`{\bf UnoCollG}`$ の対象を順序無しコレクション〈unordered collection〉と呼びます。
次のような圏の同型(同値より強い)があります。
$`\quad {\bf UnoCollG} \cong \mrm{Core}({\bf FinSet}) \In {\bf CAT}`$
つまり、順序無しコレクションは単なる有限集合と同一視できます。
$`n`$次対称群 $`\mrm{Aut}(\bar{n})`$ の要素〈群元〉で、次の形のものを考えます。
$`\quad 1 \mapsto 2\\
\quad 2 \mapsto 3\\
\quad \cdots \\
\quad n - 1 \mapsto n\\
\quad n \mapsto 1
`$
この要素から生成される $`\mrm{Aut}(\bar{n})`$ の部分群を $`\mrm{Cyc}(\bar{n})`$ とします。$`\mrm{Cyc}(\bar{n})`$ は $`{\bf Z}/n{\bf Z}`$ の足し算の群と同型です。
その対称性群が $`\mrm{Cyc}(\bar{n})`$ であるコレクション達を対象類とする $`{\bf CollG}`$ の部分亜群を $`{\bf CycCollG}`$ とします。部分亜群 $`{\bf CycCollG}`$ の対象を循環コレクション〈cyclic collection〉と呼びます。
3つのコレクション亜群を挙げました。
- $`{\bf OrdCollG}`$ 順序コレクション達の亜群
- $`{\bf UnoCollG}`$ 順序無しコレクション達の亜群
- $`{\bf CycCollG}`$ 循環コレクション達の亜群
よく現れるコレクションはこの三種類だと思います。
シーケンス
$`X = (\u{X}, \mrm{Enum}(X))`$ をコレクションとして、$`\mrm{Enum}(X)`$ の要素(同型写像)の逆写像達からなる集合を $`\mrm{Seq}(X)`$ とします。つまり:
$`\quad s \in \mrm{Seq}(X) \Iff s^{-1} \in \mrm{Enum}(X)`$
$`\mrm{Seq}(X)`$ の要素を、コレクション $`X`$ のシーケンス〈sequence〉と呼ぶことにします。シーケンスは、$`\u{X}`$ の要素を重複なく全部一列に並べたモノです。高校数学では順列と呼んでいたモノです。
$`\mrm{Enum}(X)`$ と $`\mrm{Seq}(X)`$ は、集合として同型だし、片一方を与えればもう一方は作れます。したがって、シーケンスの集合 $`\mrm{Seq}(X)`$ をコレクションの定義に使ってもかまいません。1つのシーケンスと対称性群の組でもコレクションが定義できます。
$`\mrm{Seq}(X) \subseteq \mrm{Iso}(\bar{n}, \u{X})`$ なので、シーケンスの集合には対称性群 $`\mrm{Sym}(X)`$ が左から作用します。「左から」は図式順結合記号を使っていることを前提としての左右です。
列挙に関して言えることはシーケンスに関しても言えます。例えば:
- 順序コレクションのシーケンスは唯一つだけある。
- 順序なしコレクションのシーケンスはたくさん($`n!`$ 個)ある。ひとつのシーケンスに任意の置換($`\mrm{Aut}(\bar{n})`$ の要素)を施して(左作用させて)もシーケンスである。
- 循環シーケンスのシーケンスは $`n`$ 個ある。ひとつのシーケンスに大域的循環置換($`\mrm{Cyc}(\bar{n})`$ の要素)を施して(左作用させて)もシーケンスである。
シーケンスを具体的に書くときは、リストと同じく丸括弧囲みカンマ区切りにします。
$`\quad (x_1, \cdots, x_n) \:\text{ where } x_i \in \u{X}`$
同じ要素が2回出現することはありません。
色パレット
色パレットのアイディアは、ハックニー/ロバーツォン/ヤウ〈Philip Hackney, Marcy Robertson, Donald Yau〉とレイノア〈Sophie Raynor〉によるもので、型、極性〈符号〉、向きなどをまとめて扱うための便利なツールです。色パレットについては、次の記事で述べています。
内容的な変更はありませんが、ここでは、符号関数を中心とした形の定義を提示します。習慣により色パレットはフラクトゥール体〈ドイツ文字〉で表します。
色パレット〈color palette〉 $`\cpal{C}`$(フラクトゥール体 C)は次の構成素からなります。
- 集合 $`\u{\cpal{C}}`$ (台集合)
- 関数 $`\mrm{sign}_\cpal{C} : \u{\cpal{C}} \to \{+, -, 0\}`$
- 写像 $`(-) : \u{\cpal{C}} \to \u{\cpal{C}}`$ (マイナス記号を前置演算子として使う)
ここで、集合 $`\{+, -, 0\}`$ は単に3つの記号からなる集合ですが、$`\{+1, -1, 0\}\subset {\bf Z}`$ のように解釈することもあります。不等号や正・負などの言葉が出てきたら、$`{\bf Z}`$ の要素として解釈しています。
要素 $`c \in \u{\cpal{C}}`$ を色〈color〉と呼び、$`\mrm{sign}_\cpal{C}(c)`$ を $`c`$ の符号〈sign〉といいます。$`c \in \u{\cpal{C}}`$ に対して $`-c`$ を $`c`$ の否定〈negation〉と呼びます。
色パレットは次の条件〈公理〉を満たす必要があります。
- $`\forall c\in \u{\cpal{C}}.\, -(-c) = c`$ (否定は対合的)
- $`\forall c\in \u{\cpal{C}}.\, \mrm{sign}_\cpal{C}(-c) = - \mrm{sign}_\cpal{C}(c)`$ (否定の符号は反対になる)
色の符号により次の言い方もします。
- $`\mrm{sign}_\cpal{C}(c) \gt 0 \Iff`$ 色 $`c`$ は正の色
- $`\mrm{sign}_\cpal{C}(c) = 0 \Iff`$ 色 $`c`$ は中性〈neutral〉
- $`\mrm{sign}_\cpal{C}(c) \ge 0 \Iff`$ 色 $`c`$ は非負の色
- $`\mrm{sign}_\cpal{C}(c) \lt 0 \Iff`$ 色 $`c`$ は負の色
正の色を否定すると負の色になりますが、非負の色を否定して負になるとは限りません。中性(符号がゼロの)色があるかも知れないからです。中性の色は否定しても中性です。
色パレットの台集合の部分集合を次のように定義します。
- $`\u{\cpal{C}}_{\gt 0} := \{ c \in \u{\cpal{C}} \mid \mrm{sign}_\cpal{C}(c) \gt 0 \}`$
- $`\u{\cpal{C}}_{= 0} := \{ c \in \u{\cpal{C}} \mid\mrm{sign}_\cpal{C}(c) = 0 \}`$
- $`\u{\cpal{C}}_{\ge 0} := \{ c \in \u{\cpal{C}} \mid\mrm{sign}_\cpal{C}(c) \ge 0 \}`$
- $`\u{\cpal{C}}_{\lt 0} := \{ c \in \u{\cpal{C}} \mid\mrm{sign}_\cpal{C}(c) \lt 0 \}`$
集合 $`A`$ に対して、自明な色パレット $`\cpal{A}`$(フラクトゥール体 A)を定義できます。
- $`\u{\cpal{A}} := A`$
- $`\mrm{sign}_{\cpal{A}}(a) = 0 \:\text{ for any }a\in A`$
- $`-a = a \:\text{ for any }a\in A`$
通常、集合 $`A`$ と自明な色パレット $`\cpal{A}`$ は同一視されます。
集合 $`A`$ に対して、次の色パレット $`\cpal{D}`$ (フラクトゥール体 D、符号付きダブル)はよく使われます。
- $`\u{\cpal{D}} := (\{+\}\times A) \cup (\{-\}\times A)`$
- $`\mrm{sign}_{\cpal{D}}( (+, a) ) = +,\; \mrm{sign}_{\cpal{D}}( (-, a) ) = - \: \text{ for any }a\in A`$
- $`-(+ , a) = (-, a),\; -(-, a) = (+, a) \:\text{ for any }a\in A`$
$`A`$ からこのようにして作った色パレット $`\cpal{D}`$ (符号付きダブル)を $`\pm A`$ と書きます。$`\pm A`$ に中性の色はありません。
色付きコレクション
$`\cpal{C}`$ を色パレットとします。$`X`$ をコレクションとして、このコレクションへの色付け〈coloring〉とは次の形の写像です。
$`\quad \gamma : \u{X} \to \u{\cpal{C}} \In {\bf Set}`$
$`\u{X}`$ は有限集合ですが、$`\u{\cpal{C}}`$ は有限とは限りません。ときに $`\u{\cpal{C}}`$ は小さくない集合のこともありますが、今は小さい集合だと仮定します。
色付けには特に制限・条件がないので、色パレット $`\cpal{C}`$ によるコレクション $`X`$ への色付けの全体は次の集合になります。
$`\quad \mrm{Map}(\u{X}, \u{\cpal{C}}) \;\in |{\bf Set}|`$
色パレットは固定するとして、コレクションと色付けを一緒にした構造 $`(X, \gamma)`$ を色付きコレクション〈colored collection〉と呼びます。色付きコレクションを、とりあえずここでは(一時的かも知れない) $`\ccol{x}`$ などのボールド体小文字で表すことにします。色付きコレクション $`\ccol{x}`$ は次のように書きます。
$`\quad \ccol{x} = (\u{\ccol{x}}, \gamma_\ccol{x})`$
ここで、$`\u{\ccol{x}}`$ は台であるコレクション、$`\gamma_\ccol{x}`$ は色付け関数です。
色付きコレクションのあいだの同型射〈isomorphism〉は、色付けを保存するコレクション同型射です。$`f : \ccol{x} \to \ccol{y}`$ が色付きコレクションのあいだの同型射のとき、台であるコレクションのあいだの同型射も、台コレクションの台である有限集合のあいだの同型射も同じ記号をオーバロードすることにします。このオーバロードの約束のもとで、次の図式は可換になります。
$`\require{AMScd}
\quad \begin{CD}
\u{\u{\ccol{x}}} @>{f}>> \u{\u{\ccol{y}}}\\
@V{\gamma_\ccol{x}}VV @VV{\gamma_\ccol{y}}V\\
\u{\cpal{C}} @= \u{\cpal{C}}
\end{CD}\\
\quad \text{commutative in }{\bf Set}
`$
色付きコレクション達の亜群は、$`\cpal{C}\text{-colr}`$ を前置した名前にします。
- $`\cpal{C}\text{-colr}{\bf CollG}`$ 色付きコレクションの亜群
- $`\cpal{C}\text{-colr}{\bf OrdCollG}`$ 色付き順序コレクション達の亜群
- $`\cpal{C}\text{-colr}{\bf UnoCollG}`$ 色付き順序無しコレクション達の亜群
- $`\cpal{C}\text{-colr}{\bf CycCollG}`$ 色付き循環コレクション達の亜群
色付きシーケンス
$`\ccol{x} = (\u{\ccol{x}}, \gamma_\ccol{x})`$ を色付きコレクション、台のコレクションを $`X := \u{\ccol{x}}`$ とします。コレクション $`X`$ のシーケンス $`x \in \mrm{Seq}(X)`$ をひとつ選ぶと、それは次のリストの形に書けます。
$`\quad x = (x_1, \cdots, x_n)`$
このシーケンス表示に色付けの情報も付け足します。色付け関数 $`\gamma_\ccol{x}`$ を $`\gamma`$ と略記することにして、次の形を使います。
$`\quad (x_1: \gamma(x_1), \cdots, x_n: \gamma(x_n))`$
実例を挙げましょう。色の集合は $`\pm \{r, g, b\}`$ とします。要素をすべて列挙すると:
$`\quad \{ (+,r),(+,g),(+,b),(-,r),(-,g),(-,b) \}`$
コレクション $`X`$ は順序無しコレクション(単なる有限集合)だとして、 $`\{a, e, d, c, b\}`$ とします(んっ? 色の集合と要素 $`b`$ がかぶった、けど、まーいいとします)。順序無しコレクションに全順序を与えることをアンカーリング〈anchoring〉といいます。ここでのアンカーリングは常識的アルファベット順だとしましょう。
$`\quad a \lt b \lt c \lt d \lt e`$
コレクションをアンカーすることは、そのコレクションのシーケンスを1つ選ぶことと同じです。あるいは、コレクションの列挙を1つ選ぶことだと言っても同じです。アンカーリングにより、コレクションはシーケンスに置き換わるので、リスト形式で書けます。
$`\quad (a, b, c, d, e)`$
このリストに色付け情報を添えることもできます。
$`\quad (a:(-, r), b:(+, r), c:(+, b), d:(-, g), e:(-, r))`$
もし、アルファベット順の逆順でアンカーしたとすると、リストの形は変わりますが、色付け情報に変化はありません。
$`\quad (e:(-, r), d:(+, g), c:(+, b), b:(+, r), a:(-, r) )`$
異なるアンカーリングのあいだは対称群による群作用で結ばれます。対称群の作用でリストを置換しても、同じ色付きコレクションを表現します。
もしコレクション $`X`$ が順序付きコレクション(有限全順序集合)だとすれば、リストとしての書き方は唯一つで、色付け情報を添えたリスト(色付きシーケンス)も唯一つです。
色付きシーケンスの描き方
前節の色付きコレクションの事例を絵に描きましょう。台コレクションは順序無しコレクションで、コレクションの台集合 は $`\{a, e, d, c, b\}`$ です。アルファベット順でアンカーして、色付け情報を添えます。
$`\quad (a:(-, r), b:(+, r), c:(+, b), d:(-, g), e:(-, r))`$
概念としての色(テクニカルターム)は、描画ではプラス・マイナスの記号と色(日常語、Red, Green, Blue)との組み合わせになります。アンカーリングで順番が付いているので、矢印が付いた線の上に、項目を順番に並べます。次のようになります。
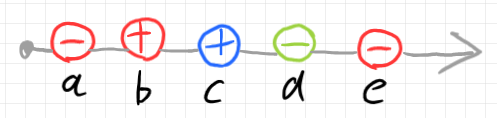
必ずしも左から右に配置する必要はありません。
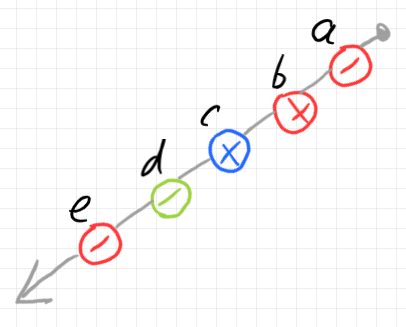
あるいは、キャンバスに向きが決まっているなら矢印は不要です。
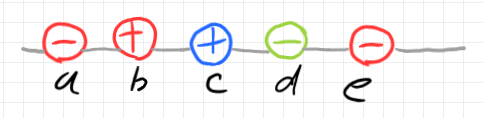
直線状の配置ではなくて、円周の上に項目を並べてもかまいません。
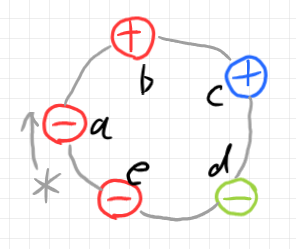
円周配置の場合、スタートの位置と時計回りか反時計回りかの指示が必要です。グレーのアスタリスクと矢印がスタート位置と時計回りであることを示しています。
プラス・マイナスを、入出力の極性だと解釈しましょう。マイナスが入力側ポート、プラスが出力側ポートです。事例の色付きシーケンス(色付きコレクションをアンカーした結果)を通常のストリング図の描き方(描画方向は上から下)で描くと次のようになります。
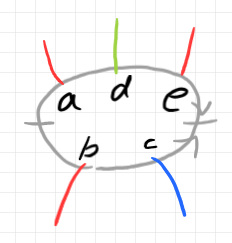
コレクションの要素がポートラベルになり、ポートに付与された色(テクニカルターム)がワイヤーの極性(入出力の別)と型(見た目での色)の情報となります。アンカー(ポートの全順序付け)がされているので、入力側(上側)も出力側(下側)も左から右への順番で描いています。
この記事冒頭で言った「ボックスは、色付きコレクションの視覚化なのだとみなすのが良さそうです」とは、今説明したような意味です。