高階関手の計算：米田と淡中の周辺 - 檜山正幸のキマイラ飼育記 (はてなBlog)

高階関手〈higher-order functor〉は、高次圏のn-関手〈n-functor | higher functor〉のことではなくて、高階関数と同様に、関手（または自然変換）を引数にしたり、関手（または自然変換）を返すような関手のことです。高階関数の計算が、関数を射とする圏のデカルト閉構造を利用した計算であるように、高階関手の計算も、圏の2-圏のデカルト閉構造を利用した計算です。

高階関数の場合と違う点は、関手〈1-射 | (2, 0)-変換手〉だけでなくて自然変換〈2-射 | (2, 1)-変換手〉もあること、それと、「反対圏と反変関手はややこしい」で述べた向きを考慮する必要があり、そこがけっこうややこしいことです。

この記事は、「反対圏と反変関手はややこしい」の続き（やり残しの記述）であり、「大域米田の補題」の敷衍にもなっています。例えば、この記事で導入する記法を使うと、大域米田の補題は次のように書けます。

$`\quad よ^\vee[\widetilde{よ}] \cong た`$

'$`よ`$' は“米田の「よ」”、'$`た`$' は“淡中の「た」”です。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\o}[1]{\overline{#1}}
\newcommand{\bs}[1]{\boldsymbol{#1}}
%\newcommand{\Imp}{ \Rightarrow }
\newcommand{\In}{ \text{ in } }
\newcommand{\op}{\mathrm{op}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\Id}{\mathrm{Id}}
\newcommand{\Rev}{\mathrm{Rev}}
\newcommand{\hyp}{\text{－}}
%\newcommand{\twoto}{\Rightarrow}
\newcommand{\Iff}{\Leftrightarrow}
\newcommand{\For}{\text{For } }
`$

内容：

記法の約束
反対圏と反変関手
ホム関手と米田埋め込み
評価関手と淡中埋め込み
大域米田の補題

記法の約束

$`\o{\bf CAT}`$ は、ほんとの反変関手も含む圏の2-圏です（詳しくは「反対圏と反変関手はややこしい」参照）。$`\o{\bf CAT}`$ のホム圏には、共変関手達から生成される充満部分圏と、反変関手達から生成される充満部分圏が含まれます。

$`\o{\bf CAT}^+(\cat{C}, \cat{D})`$ ：対象は共変関手
$`\o{\bf CAT}^-(\cat{C}, \cat{D})`$ ：対象は反変関手（ホム圏に閉じ込めて考える）
$`\o{\bf CAT}(\cat{C}, \cat{D}) = (\o{\bf CAT}^+(\cat{C}, \cat{D})\cup \o{\bf CAT}^-(\cat{C}, \cat{D}) )`$

$`\o{\bf CAT}`$ のホム圏が、共変関手と反変関手の両方を含むことを強調したいとき、次のようにも書きます。

$`\quad \o{\bf CAT}(\cat{C}, \cat{D}) = \o{\bf CAT}^\pm (\cat{C}, \cat{D})`$

$`|{\bf CAT}| = |\o{\bf CAT}|`$ で、圏のペアごとに $`{\bf CAT}(\cat{C},\cat{D})\subseteq \o{\bf CAT}(\cat{C},\cat{D})`$ となり、$`{\bf CAT}`$ は、$`\o{\bf CAT}`$ の広い〈対象類を共有する〉部分圏です。

反対圏と反変関手

この節で、「反対圏と反変関手はややこしい」で少し残っていた事を片付けます。

$`\o{\bf CAT}`$ は単に厳密2-圏であるだけでなく、次の構造を持ちます。

厳密に対合的な写像〈strictly involutive map〉 $`(\hyp)^\op : |\o{\bf CAT}| \to |\o{\bf CAT}|`$ を持つ。
対象〈圏〉でインデックス付けられた1-射〈反変関手〉の族 $`\mrm{Rev}_\cat{C}: \cat{C} \overset{-}{\to} \cat{C}^\op \In \o{\bf CAT}`$ を持つ。これらの1-射は可逆で $`\mrm{Rev}_{\cat{C}}^{-1} = \mrm{Rev}_{\cat{C}^\op}`$ 。

裏返し関手 $`\mrm{Rev}_\hyp`$ をプレ結合／ポスト結合することにより、「反変関手 ←→ 共変関手」の入れ替えができます。

$`\mrm{Rev}_{\cat{C}^\op}`$ のプレ結合は、$`\o{\bf CAT}^-(\cat{C}, \cat{D}) \overset{+}{\to} \o{\bf CAT}^+(\cat{C}^\op, \cat{D})`$ の圏同型を導く。
$`\mrm{Rev}_{\cat{C}^\op}`$ のプレ結合は、$`\o{\bf CAT}^+(\cat{C}, \cat{D}) \overset{+}{\to} \o{\bf CAT}^- (\cat{C}^\op, \cat{D})`$ の圏同型を導く。
$`\mrm{Rev}_{\cat{D}}`$ のポスト結合は、$`\o{\bf CAT}^-(\cat{C}, \cat{D}) \overset{-}{\to} \o{\bf CAT}^+(\cat{C}, \cat{D}^\op)`$ の反変圏同型を導く。
$`\mrm{Rev}_{\cat{D}}`$ のポスト結合は、$`\o{\bf CAT}^+(\cat{C}, \cat{D}) \overset{-}{\to} \o{\bf CAT}^- (\cat{C}, \cat{D}^\op,)`$ の反変圏同型を導く。

裏返し関手のポスト結合が反変になること（自然変換の向きを反転させること）は、「反対圏と反変関手はややこしい」で説明しています。

次の記法を使うことにします。

$`\quad [\cat{C}, \cat{D}]^\pm := ([\cat{C}, \cat{D}]^+ \cup [\cat{C}, \cat{D}]^-) = \o{\bf CAT}^\pm(\cat{C}, \cat{D}) = \o{\bf CAT}(\cat{C}, \cat{D})`$

上の箇条書きの前半2つをまとめて次のように書きます。

$`\quad \bs{\Phi}_{\cat{C}, \cat{D}} = (\mrm{Rev}_{\cat{C}^\op} * \hyp) : [\cat{C}, \cat{D}]^\pm \overset{+}{\to} [\cat{C}^\op, \cat{D}]^\pm \In \o{\bf CAT}
`$

後半2つをまとめて次のように書きます。

$`\quad \bs{\Psi}_{\cat{C}, \cat{D}} = (\hyp * \mrm{Rev}_{\cat{D}}) : [\cat{C}, \cat{D}]^\pm \overset{-}{\to} [\cat{C}, \cat{D}^\op]^\pm \In \o{\bf CAT}
`$

$`\bs{\Phi}`$ も $`\bs{\Psi}`$ も、関手の変性〈variance〉を入れ替えます。$`\bs{\Psi}`$ は自然変換の向きを反転させます。

「層化ストリング図 // 裏返し反変関手」で導入した記法を使うと：

$`\For F\in [\cat{C}, \cat{D}]^\pm\\
\quad {^\mrm{rev} F} := \bs{\Phi}(F) = \mrm{Rev}_{\cat{C}^\op} * F \;\in [\cat{C}^\op, \cat{D}]^\pm\\
\quad { F^\mrm{rev}} := \bs{\Psi}(F) = F * \mrm{Rev}_{\cat{D}} \;\in [\cat{C}, \cat{D}^\op]^\pm
`$

$`\bs{\Phi}`$ と $`\bs{\Psi}`$ の結合として、$`\bs{\Theta}`$ を定義します。

$`\xymatrix{
{}
& {[\cat{C}^\op, \cat{D}]^\pm} \ar[dr]^{\Psi}_{-}
& {}
\\
{[\cat{C}, \cat{D}]^\pm} \ar[ur]^{\Phi}_{+} \ar[rr]^{\Theta}_{-}
& {}
& {[\cat{C}^\op, \cat{D}^\op]^\pm}
}`$

次のように直接定義することもできます。

$`\For F \in | [\cat{C}, \cat{D}]^\pm |\\
\quad \bs{\Theta}_{\cat{C}, \cat{D}}(F) := \mrm{Rev}_{\cat{C}^\op} * F * \mrm{Rev}_\cat{D}
\; \in | [\cat{C}^\op, \cat{D}^\op]^\pm|\\
\For \alpha : F \to G \In [\cat{C}, \cat{D}]^\pm \\
\quad \bs{\Theta}_{\cat{C}, \cat{D}}(\alpha) := \mrm{Rev}_{\cat{C}^\op} * \alpha * \mrm{Rev}_\cat{D}\\
\qquad : \mrm{Rev}_{\cat{C}^\op} * F * \mrm{Rev}_\cat{D} \to \mrm{Rev}_{\cat{C}^\op} * G * \mrm{Rev}_\cat{D} \In [\cat{C}^\op, \cat{D}^\op]^\pm
`$

また、次のように定義しても同じです。

$`\xymatrix{
{}
& {[\cat{C}, \cat{D}^\op]^\pm} \ar[dr]^{\Phi}_{+}
& {}
\\
{[\cat{C}, \cat{D}]^\pm} \ar[ur]^{\Psi}_{-} \ar[rr]^{\Theta}_{-}
& {}
& {[\cat{C}^\op, \cat{D}^\op]^\pm}
}`$

「大域米田の補題」で（一時的に）導入した記法を使うと：

$`\For F\in |[\cat{C}, \cat{D}]^\pm |\\
\quad \widetilde{ F} := \bs{\Theta}_{\cat{C},\cat{D}}(F) = \mrm{Rev}_{\cat{C}^\op} * F * \mrm{Rev}_\cat{D} \;\in | [\cat{C}^\op, \cat{D}^\op]^\pm |
`$

問題は、互いに対応している関手を区別するか同一視するか？です。互いに対応しているペアは：

$`F:\cat{C} \overset{-}{\to} \cat{D} \longleftrightarrow {^\mrm{rev}F}:\cat{C}^\op \overset{+}{\to} \cat{D}`$
$`F:\cat{C} \overset{-}{\to} \cat{D} \longleftrightarrow {F^\mrm{rev}}:\cat{C} \overset{+}{\to} \cat{D}^\op`$
$`{^\mrm{rev}F}:\cat{C}^\op \overset{+}{\to} \cat{D} \longleftrightarrow {F^\mrm{rev}}:\cat{C} \overset{+}{\to} \cat{D}^\op`$
$`F:\cat{C} \overset{+}{\to} \cat{D} \longleftrightarrow \widetilde{F}:\cat{C}^\op \overset{+}{\to} \cat{D}^\op`$

関手だけを考えているなら同一視してもよさそうです。が、$`\bs{\Psi}`$ と $`\bs{\Theta}`$ は自然変換の向きを反転するので、自然変換も考えるときは区別しないと混乱するでしょう。

ホム関手と米田埋め込み

ホム関手を $`\o{\bf CAT}`$ 内で考えたものは次のように書きます。

$`\quad \o{\mrm{Hom}}_\cat{C} : \cat{C}, \cat{C} \overset{-, +}{\to} {\bf Set}
\In \o{\bf CAT}
`$

ここで、矢印の上の $`-, +`$ は、第一引数に関して反変で、第二引数に関して共変であることを示します。

$`\mrm{Rev}_{\cat{C}^\op} \times \mrm{Id}_\cat{C}`$ をプレ結合した関手は次です。

$`\quad \mrm{Hom}_\cat{C} : \cat{C}^\op, \cat{C} \overset{+, +}{\to} {\bf Set}
\In \o{\bf CAT}
`$

これは $`{\bf CAT}`$ 内で考えることができるので：

$`\quad \mrm{Hom}_\cat{C} : \cat{C}^\op \times \cat{C} {\to} {\bf Set} \In {\bf CAT}
`$

このホム関手を左カリー化／右カリー化します。関手と自然変換のカリー化については次の過去記事で述べています。

関手・自然変換のカリー化

ホム関手の左カリー化が米田埋め込み〈Yoneda embedding〉で、右カリー化が余米田埋め込み〈coYoneda embedding〉です。

$`\quad {^\cat{C}よ} := {^\cap (\mrm{Hom}_\cat{C})} : \cat{C} \to [\cat{C}^\op, {\bf Set}]
\In {\bf CAT}\\
\quad {^\cat{C}よ^\vee} := {(\mrm{Hom}_\cat{C})^\cap } : \cat{C}^\op \to [\cat{C}, {\bf Set}]
= [{\bf Set}\leftarrow \cat{C}] \In {\bf CAT}
`$

米田埋め込みの色々な記法は、次の過去記事にまとめてあります。

米田埋め込みの書き方（色々ありすぎ）

ここで使うのは「よ」記法です。

$`\text{ハイフン記法}`$	$`\text{「よ」記法}`$
$`\cat{C}(\hyp, B)`$	$`{^\cat{C}よ}^B = {^\cat{C}よ}[B]`$
$`\cat{C}(A, \hyp)`$	$`{^\cat{C}よ}^\vee_A = {^\cat{C}よ}^\vee[A]`$

引数を上付き下付きで渡すと視認性が悪くなるときがあるので、ブラケットも使います。

$`{^\cat{C}よ}`$ に対象を渡せば関手で、射を渡せば自然変換になります。

$`\For A\in |\cat{C}|\\
\quad {^\cat{C}よ}[A] \in [\cat{C}^\op, {\bf Set}]\\
\For f:A \to B \In \cat{C}\\
\quad {^\cat{C}よ}[f] : {^\cat{C}よ}[A] \to {^\cat{C}よ}[B] \In [\cat{C}^\op, {\bf Set}]
`$

自然変換 $`{^\cat{C}よ}[f]`$ を具体的に記述すれば：

$`\For X \in |\cat{C}|\\
\quad {^\cat{C}よ}[f]_X : ({^\cat{C}よ}[A])(X) \to ({^\cat{C}よ}[B])(X)\\
\quad \For u \in ({^\cat{C}よ}[A])(X) = \cat{C}(X, A)\\
\qquad ({^\cat{C}よ}[f]_X)(u) := u; f = f\circ u \; \in ({^\cat{C}よ}[B])(X) = \cat{C}(X, B)
`$

$`{^\cat{C}よ}[f]`$ は、$`f`$ のポスト結合による前送りなので、$`f_*`$ と簡潔に書くこともあります。

同様に、$`{^\cat{C}よ^\vee}[f]`$ は、$`f`$ のプレ結合による引き戻しとなり、$`f^*`$ とも書きます。

評価関手と淡中埋め込み

評価関手は、関手／自然変換に引数を渡して値を求める行為を再び関手とみなしたものです。左から引数を渡す場合の評価関手は次のように書きます。

$`\quad \mrm{LEv}_{\cat{C}, \cat{D}} : \cat{C} \times [\cat{C}, \cat{D}] \to \cat{D} \In {\bf CAT}`$

左評価関手 $`\mrm{LEv}`$ は、$`\cat{C}`$ の射や $`[\cat{C}, \cat{D}]`$ の射〈自然変換〉に対しても定義できて、二項関手〈双関手〉になります。

左評価関手を左カリー化すると恒等関手になってしまうので右カリー化を考えます。

$`\quad ( \mrm{LEv}_{\cat{C}, \cat{D}} )^\cap : \cat{C} \to [ [\cat{C}, \cat{D}], \cat{D}]
\In {\bf CAT}
`$

特に、次の場合に得られる左評価関手の右カリー化を淡中埋め込み〈Tannaka embedding〉と呼ぶことにします。

$`\quad {^\cat{C} た} := ( \mrm{LEv}_{ \cat{C}^\op, {\bf Set} } )^\cap :
\cat{C}^\op \to [ [\cat{C}^\op, {\bf Set}], {\bf Set}]
\In {\bf CAT}
`$

「淡中埋め込み」は一般的な用語ではありませんが、淡中双対性〈Tannaka duality〉／淡中再構成〈Tannaka reconstruction〉で重要な役割りを演じる関手です。

淡中埋め込みに“淡中の「た」”を使いましたが、最近、丹原加群の構成素として「た」が使われる（下の画面コピー）ので注意が必要です。

https://arxiv.org/abs/2210.13443より：

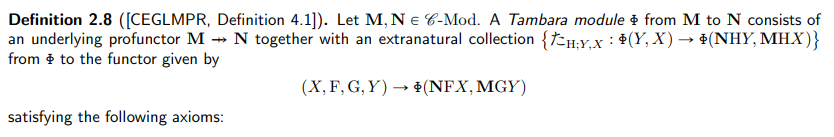
今は左評価関手を使いましたが、右評価関手の左カリー化が淡中埋め込みだとしても同じことです。

大域米田の補題

大域米田の補題と関連する計算例については、次の記事で書きました。

大域米田の補題の主張は次のように言えます。

淡中埋め込みは、二階の（あるいは二回の／二重の）米田埋め込みとして表せる。

このことを以下に説明します。

まず、局所的な〈pointwiseの〉米田の補題は次のようです。

$`\quad [\cat{C}^\op, {\bf Set}]({^\cat{C} よ}[A], F) \cong F(A) \In {\bf Set}
`$

関手圏〈前層の圏〉 $`[\cat{C}^\op, {\bf Set}]`$ を $`\cat{C}^\wedge`$ と短く書いて、右辺は左評価関手を使って書きましょう。すると：

$`\quad \cat{C}^\wedge ({^\cat{C} よ}[A], F) \cong \mrm{LEv}_{\cat{C}^\op, {\bf Set}}(A, F) \In {\bf Set}
`$

ここで、登場している関手のプロファイル（域と余域）を調べてみます。

$`{^\cat{C} よ} : \cat{C} \to \cat{C}^\wedge \In {\bf CAT}`$
$`\mrm{Hom}_{\cat{C}^\wedge} : (\cat{C}^\wedge)^\op \times \cat{C}^\wedge \to {\bf Set} \In {\bf CAT}`$
$`\mrm{LEv}_{\cat{C}^\op, {\bf Set}} : \cat{C}^\op \times \cat{C}^\wedge \to {\bf Set} \In {\bf CAT}`$

関手の結合が整合的にできるためには、$`{^\cat{C} よ}`$ をそのままは使えません。次のように組み立てます。

$`\widetilde{^\cat{C} よ} : \cat{C}^\op \to (\cat{C}^\wedge)^\op \In {\bf CAT}`$
$`\mrm{Hom}_{\cat{C}^\wedge} : (\cat{C}^\wedge)^\op \times \cat{C}^\wedge \to {\bf Set} \In {\bf CAT}`$
$`(\widetilde{^\cat{C} よ}\times \mrm{Id}_{\cat{C}^\wedge}) * \mrm{Hom}_{\cat{C}^\wedge} : \cat{C}^\op \times \cat{C}^\wedge \to {\bf Set} \In {\bf CAT}`$

無名ラムダ変数（ハイフン）を使って書けば：

$`\quad \cat{C}^\wedge ({^\cat{C} よ}[\hyp], \hyp) \cong \mrm{LEv}_{\cat{C}^\op, {\bf Set}}(\hyp, \hyp) : \cat{C}^\op \times \cat{C}^\wedge \to {\bf Set} \In {\bf CAT}
`$

関手圏を使って書けば：

$`\quad \cat{C}^\wedge ({^\cat{C} よ}[\hyp], \hyp) \cong \mrm{LEv}_{\cat{C}^\op, {\bf Set}}(\hyp, \hyp) \In [\cat{C}^\op \times \cat{C}^\wedge , {\bf Set} ]
`$

ここで、上記同型の両辺を右カリー化します。左辺の右カリー化は、$`\cat{C}^\wedge (\hyp, \hyp)`$ の右カリー化に $`{^\cat{C} よ}`$ をプレ結合したものです。ところが、$`\cat{C}^\wedge (\hyp, \hyp)`$ の右カリー化は余米田埋め込みなので、左辺の右カリー化は次のように書けます。

$`\quad ( (\widetilde{^\cat{C} よ}\times \mrm{Id}_{\cat{C}^\wedge}) * \mrm{Hom}_{\cat{C}^\wedge} )^\cap\\
= \widetilde{^\cat{C} よ} * ( \mrm{Hom}_{\cat{C}^\wedge} )^\cap \\
= \widetilde{^\cat{C} よ} * ({^{\cat{C}^\wedge} よ^\vee})\\
= ({^{\cat{C}^\wedge} よ^\vee}) [ \widetilde{^\cat{C} よ}[\hyp] ]
`$

一方の右辺は、左評価関手の右カリー化になるので淡中埋め込み $`{^\cat{C} た}`$ です。したがって、大域米田の補題は次の同型の形に書けます。

$`\quad ({^{\cat{C}^\wedge} よ^\vee}) [ \widetilde{^\cat{C} よ}[\hyp] ] \cong
{^\cat{C} た} \In [\cat{C}^\op, [\cat{C}^\wedge , {\bf Set} ] ]
`$

添字として付いている $`\cat{C}`$ や $`\cat{C}^\wedge`$ を省略すると：

$`\quad よ^\vee [ \widetilde{ よ} ] \cong
{ た} \In [\cat{C}^\op, [\cat{C}^\wedge , {\bf Set} ] ]
`$

右辺の淡中埋め込みは、外側の前層レベルの余米田埋め込みに、もとの圏の米田埋め込みを代入して得られることが分かりました。余米田埋め込みに米田埋め込みを代入したものは二階の（あるいは二回の／二重の）米田埋め込みと呼んでいいでしょう。

再度繰り返すと：