古典的微分幾何・ベクトル解析のモダン化：因習的微分幾何とその構造

久々の「モダン化」シリーズの記事です。以下のエントリーがシリーズのハブになっています。

古典的微分幾何・ベクトル解析のモダン化：ラムダ記法の利用

モダンの反対語として、「因習的」を使うことにします。モダンではない、因習的微分幾何のどこが何故によろしくないかを述べます。因習による弊害は微分幾何に限らないようです。比較のために、確率・統計の因習にも少し触れます。

内容：

因習的とは
チャートとチャートの族
座標変換
因習的オーバーロード
因習の淵源と意義

因習的とは

「モダンではない」の意味で「古典的」とか「伝統的」とかを使ってきました。が、これらの言葉には「守るべき良きもの」という印象があります。「古式」なんて言葉も使いましたが、これだって「古き良き」の意味で使われます。

僕は「モダンではないもの」に批判的なので、称賛・肯定の意味がなく貶める言葉を使いたい。で、「因習的」にします。因習とは「古くから伝わり、とかく弊害を生むしきたり」ってことなので。

因習的な方法の困ったところは、重要な概念を表す用語・記法が曖昧なままに進んでしまう点です。例えば座標〈局所座標〉、これはとても重要な概念ですが、ハッキリしない記法が因習的に使われています。意味が分からないままに計算の仕方だけが解説されます。

「重要な概念がハッキリしないままに計算の仕方だけが…」んっ、ほかでもそんなことが … 因習的確率・統計では、確率変数という最重要な概念が曖昧なままに確率分布の計算の仕方が解説されます。状況はとても似ています。

	微分幾何	確率・統計
重要な概念	座標〈局所座標〉	確率変数
背後にある実体	多様体	確率空間
計算の場	Rⁿ	Rⁿ
計算の対象	前送りされた関数など	前送りされた確率測度

背後にある実体に触れずに、手前での計算が縷々〈るる〉と語られる -- それが因習的方法の特徴のようです。微分幾何とベクトル解析、そして確率・統計には、目立った因習が存在します -- 他にも因習があるかもしれません。例えば、因習的線形代数はありそうです*1。

因習的方法に共通していることは：

背後にある実体の隠蔽
過度なオーバーロード

背後にある実体とは多様体や確率空間のことです。実体の存在をまるで隠すように、Rⁿ上の代理物の計算に終始するのが因習的方法です。例え話が、「古典的微分幾何・ベクトル解析のモダン化：局所座標って何だ？ // モニタールームの孤独な男」にあります。

オーバーロードとは、言葉や記号の多義的な使用です。オーバーロードは便利な点もあります（それゆえに、プログラミング言語にも実装されます）が、過度にオーバーロードすると、ナニガナニヤラ意味不明になります。

次節以降では、微分幾何の因習的方法の実例を挙げましょう。因習的確率・統計については：

チャートとチャートの族

チャートについては、「古典的微分幾何・ベクトル解析のモダン化：局所座標って何だ？」に書いてありますが、ここで再度述べます。

Mが多様体のとき、Mのチャート〈chart〉とは次のものからなります。

Mの開集合 U
Rⁿ の開集合 C
連続で可逆（位相同型）な写像 φ:U→C

これらをまとめて書けば、φ:M⊇U→C⊆Rⁿ 、多様体Mと次元nが了解されているなら、φ:U→C 、あるいは (φ, U, C) と書くことにします。

単一のチャートではなくて、チャートの集まりが問題になります。Iを添字集合〈index set〉として、i∈I ごとにチャート (φ_i, U_i, C_i) が対応している状況を考えましょう。このようなとき、{(φ_i, U_i, C_i) | i∈I} をチャート族〈family of charts〉と呼ぶことにします。

チャート族 {(φ_i, U_i, C_i) | i∈I} が、 $\bigcup_{i\in I}$ U_i = M *2 であるときは、このチャート族をアトラス〈atlas〉と呼びます。チャートの定義域である開集合達がM全体を覆うならアトラスです。が、ここでは特にアトラスに拘らないで、単なるチャート族を扱います。

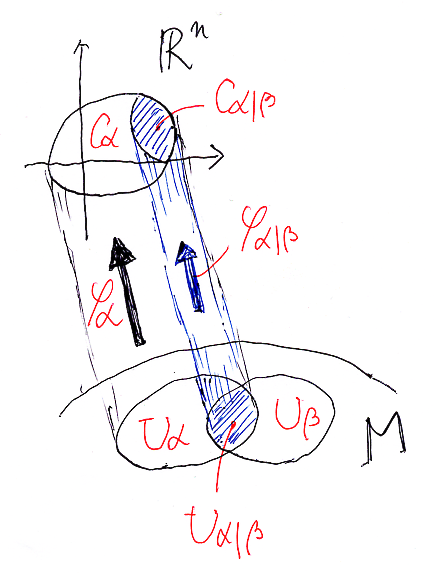
さて、チャート族 {(φ_i, U_i, C_i) | i∈I} に対して、いくつかの概念と記法を定義しておきます。以下、α, β∈I とします。

チャート φ_α : U_α → C_α を、U_α∩U_β に制限した写像 φ_α|_{U_α∩U_β} を考えます。

φ_α|_{U_α∩U_β} : U_α∩U_β → C_α

これは可逆（位相同型）とは限りませんが、余域を像集合 Im(φ_α|_{U_α∩U_β})⊆Rⁿ に制限した写像を φ_α|β と書くことにします。

φ_α|β : U_α∩U_β → Im(φ_α|_{U_α∩U_β})

φ_α|β は可逆です。さらに次の記法も導入します。

U_α|β := _{U_α∩U_β}
C_α|β := Im(φ_α|_{U_α∩U_β})

すると：

φ_α|β : U_α|β → C_α|β （可逆写像）

絵を描けば次のようです。

座標変換

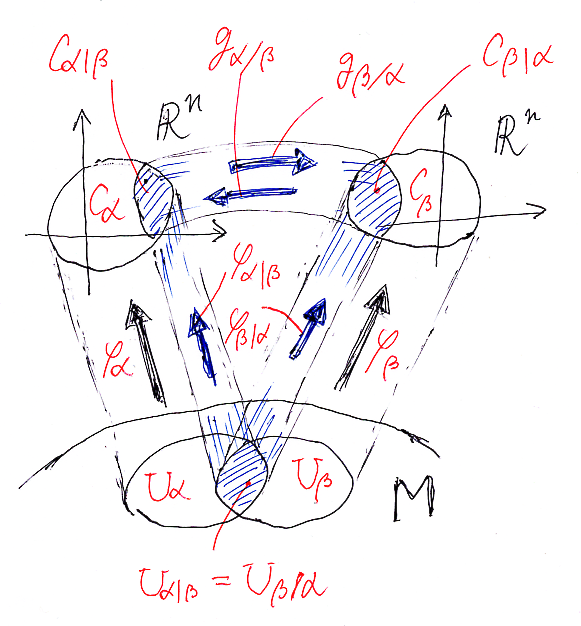
チャート族 {(φ_i, U_i, C_i) | i∈I} に対して、そのなかの2つのチャート (φ_α, U_α, C_α), (φ_β, U_β, C_β) を考えます。次の2つの写像を作れます。

φ_α|β : M⊇U_α|β → C_α|β⊆Rⁿ
φ_β|α : M⊇U_β|α → C_β|α⊆Rⁿ

U_α|β = U_β|α ですが、C_α|β = C_β|α とは限りません。

チャートのことを局所座標〈local coordinate〉とも呼びます。局所座標を単に座標〈coordinate〉とも呼びます。チャートと座標は同義語です。添字 i∈I で添字付けられた座標〈チャート〉を、座標iともいいます。

座標αから座標βへの座標変換〈change of coordinates | coordinate transformation〉 g_β/α は次のように定義します。

g_β/α := φ_β|α $\circ$ φ_α|β^-1 : C_α|β → C_β|α

φ_α|β : U_α|β → C_α|β は可逆だったので、逆写像 φ_α|β^-1 : C_α|β → U_α|β は意味を持ちます。したがって、合成〈結合〉写像 φ_β|α $\circ$ φ_α|β^-1 も意味を持ちます。

逆向きの座標変換は：

g_α/β := φ_α|β $\circ$ φ_β|α^-1 : C_β|α → C_α|β

φ_α, φ_α|β, φ_β, φ_β|α, g_β/α, g_α/β の関係を絵に描けば：

因習的オーバーロード

添字集合を I = {1, 2} とします。すると、Iを添字集合とするチャート族は、{(φ₁, U₁, C₁), (φ₂, U₂, C₂)} と書けます。番号の代わりに文字を使って I = {x, y} ならば、{(φ_x, U_x, C_x), (φ_y, U_y, C_y)} ですね。x, y でラベルされた、座標xと座標yがあることになります。

さて、ここからは、因習的方法の真骨頂(?)をお見せしましょう。とても便利（事実だが皮肉）なオーバーロードです。

まず、φ_x を x 、φ_y を y と書きます。

x:U_x→C_x
y:U_y→C_y

C_x, C_y 上を走る変数もそれぞれ x, y としましょう。U_x, U_y を走る変数を p, q とするなら：

x = x(p)
y = y(q)

変数と関数を区別しないことにしたので、pはφ_x^-1、qはφ_y^-1の意味でも使えます。

p = p(x)
q = q(y)

座標変換 g_y/x と g_x/y もそれぞれ y, x と書くことにします。

y = y(x)
x = x(y)

この y(x), x(y) の定義は：

y = y(x) = y(p(x))
x = x(y) = x(q(y))

とても短くてエレガント（事実だが皮肉）。

それだけではありません。fが多様体M上の関数 f:M→R のとき、f(p) の代わりに f(x) とも書きます。f(x) の意味は実は f $\circ$ x^-1 = f $\circ$ φ_x^-1 です*3。

文字'x'がどのくらいオーバーロードされるかと言うと：

φ_x を x と書く。
C_x 上を走る変数を x と書く。
g_x/y を x と書く。
φ_x^-1 を x と書く（f(x)の例）。

チャートに関連する諸々を、味噌も糞も一緒に、チャート〈座標〉のラベルである'x'だけで表現するわけです。そして、変数と関数の区別も曖昧なままに、座標変換や関数を組み合わせたり微分したり… ハァー（ため息）。

因習の淵源と意義

古くは、関数の入力〈引数〉変数を独立変数、関数の出力〈戻り値〉変数を従属変数と呼んでいました。さらには、「関数とは従属変数のことだ」と定義されることがありました。僕は年寄りなので、そういう記述を何度か見たことがあります。

今風の関数〈写像〉の定義からすれば、従属変数は関数の一部ではありません。ましてや、「従属変数＝関数」なんてことはあり得ません。しかし、変数によって関数を表す、変数と関数を区別しない、という因習は根強く残っています。今後とも滅びることはないでしょう。

多様体からRⁿへの座標にしろ、確率空間からRⁿへの確率変数にしろ、間違いなく関数〈写像〉です。それが、変数と関数を区別しない因習により変数扱いになり、さらに、変数名が過度にオーバーロードされる、という共通の構図が見られます。関数とその域・余域を曖昧なままに、「変数名を使ってそれら諸々をモンヤリと表す」習慣がどうも諸悪の根源のようです。

この悪い習慣が根絶やしにできないのは何故でしょう？ -- 便利だからです。φ_α, φ_α|β, φ_β, φ_β|α, g_β/α, g_α/β なんてタクサンの記号を使い分けることなく、xとyだけで済んだら簡略ですね、楽ですよね、素早く記述や計算が出来ます。オーバーロードの愛用者はいなくなりません。

事情を分かっている人には簡略で楽で手放せないのですが、最初から過度なオーバーロードを使われるとナニガナニヤラ意味不明になります。

現在においても、因習的な用語・記法にある程度は慣れる必要があるのは：