bonotakeさんと酒井さんのエントリーに反応してみる。
「有向グラフAに対して、AAを求めよ」というハナシらしいですが、問題の正確な表現を知らないので、「有向グラフの圏」、「グラフA」の定義がよくわかりません。んで、都合のいいように勝手に解釈しちゃう(苦笑)。
グラフの射は、「頂点を頂点に、辺を辺に写す(移す)」写像でしょう。もし、Aが2頂点(sとt)と1辺(sからtへのa)だけからなるとすると、グラフ射は恒等写像しかなくなってしまう(行き先の辺が見つからない)ので、Aは実は“2頂点3辺”としましょう。a以外に、sからs、tからtへの辺がある、と。
頂点xごとに、x→xである辺が指定されている有向グラフは、反射的有向グラフ(reflexive directed graph)とか呼ぶようです。"reflexive"は同値関係のreflexivity(a ≡ a)と同じような意味合いでしょう。Aが反射的だと強引に仮定して、圏の恒等射(identity)と同じように、2つの辺はids, idtと書くことにします。
順序集合としてのA
反射的有向グラフは、圏から結合(composition)を忘れた構造なので、圏の議論がかなり通用します。
さてAは、とてもやせた圏((「はじめての圏論 その第3歩:極端な圏達」参照)と同じ議論で、順序集合とみなせます(反射的有向グラフがいつでも順序集合とみなせるわけではない!)。3本の辺はそれぞれ、次の順序関係に対応します。
- s ≦ s (idsに対応)
- s ≦ t (aに対応)
- t ≦ t (idtに対応)
であるならば、f:A→A は、頂点集合(順序構造の台集合と考える)間の写像で、順序を保つもの、つまり “x ≦ y ⇒ f(x) ≦ f(y)“であるもの(単調写像)なので、次の3つですね。
- f1(s) = s, f1(t) = s
- f2(s) = s, f2(t) = t
- f3(s) = t, f3(t) = t
これらは、「頂点を頂点に、辺を辺に」(ただし、辺の向きを保つ)という定義で考えた射と同じです。
Monoto(A, A)の順序構造
順序集合と考えたAから、それ自身への単調(monotone, monotonic, order-preserving)写像の集合Monoto(A, A) = {f1, f2, f3}の上には、“f ≦ g ⇔ すべてのxに対して f(x) ≦ g(x)”として再び順序が入ります。それを列挙すると:
- f1 ≦ f1
- f1 ≦ f2
- f1 ≦ f3
- f2 ≦ f2
- f2 ≦ f3
- f3 ≦ f3
となり、これがAAの“辺”に対応するでしょう。順序を矢印で描くと、それはMonoto(A, A)を台とする順序構造の図(ハッセ図)であり、それ自身が反射的有向グラフとなっています。
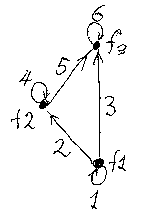
結合を忘れた圏としてのA
順序のハナシにすり替えると、だまされた感じがするかも知れないので、別な解釈を示しましょう。反射的有向グラフは“ほぼ圏”なので、圏の指数(べき)DCと同じ方法でAAを作ります。つまり、関手圏のごとくにAAを定義する、と。
AAの頂点は、「頂点を頂点に、辺を辺に」写す写像なので、先ほどのf1, f2, f3の3つ。AAの辺であるところの f1⇒f2 とかは、自然変換の類似で、f1(s)→f2(s), f1(t)→f2(t) という“Aの辺の対”だとします。結合がないので、四角形の可換性(自然性)は要求しません。より一般に、Bを任意のグラフとして、f, g:A→B、α::f⇒g:A→B の状況を絵に描けば:
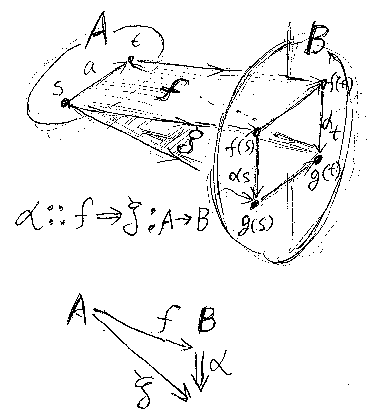
変換(あるいは変形)αによって、Bのなかでfからgへとモーフィングしていく状況*1を表現しているのが、α::f⇒g:A→B なんだけど雰囲気伝わりますか? 関手と自然変換の議論のときも、立体的な絵を描くといいですよ(例えば、http://d.hatena.ne.jp/m-hiyama-memo/20060422/1145676117)。
fi⇒fj のi, jのすべての組み合わせは3×3で9通りしかないので、列挙してみれば:
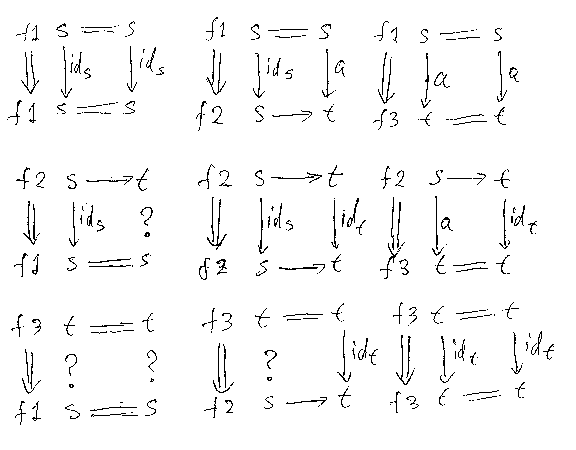
9つのうち6つが定義可能。で結局、AAは3頂点6辺の反射的有向グラフですね、やっぱり。
反射的有向グラフという仮定のもとなら、AAが3頂点6辺だという別な状況証拠もあるんだけど、なんか循環論法みたいな気もするので別エントリー(メモ編)にします。