工作員お手伝いのショー君がid:aiue3という投げやりなIDでダイアリーを書いていたようです。http://d.hatena.ne.jp/aiue3/20061120#1164006565 のなかに再帰的下向き法(recursive decent; 再帰下降法)というのが出てくるので少し補足しておきましょう。
お馴染みの算術式(arithmetic expression)を素材にします。'+'は足し算, '*'は掛け算、そして'-'は引き算ではなくて符号反転の単項演算子とします。
式 ::= 数 | 和 | 積 | 符号反転 | '(' 式 ')'
和 ::= 式 '+' 式
積 ::= 式 '*' 式
符号反転 ::= '-' 式
これでも、構文的に正しい算術式を定義できます。しかし、3 + 5 * 2 が (3 + 5) * 2 なのか 3 + (5 * 2) なのかはわかりません。我々が 3 + 5 * 2 = 3 + (5 * 2) だと常識的に判断できるのは、足し算より掛け算を優先するということをさんざんトレーニングされたからです。
優先順位を持つ演算子群を含む式の解析には演算子順位文法に基づくパーザーが便利です(このタイプのパーザージェネレータの実例を僕は知らないけど)。Prologインタプリタなどは実行時に演算子を定義可能で、前置/中置/後置の別、結合性(右結合的か左結合的か)、優先順位(を示す数値)を指定して演算子を定義すると、3 + 5 * 2 を +(3, *(5, 2)) と解釈するようなルールが動的に追加されます。
さて、aiue3ことショー君はJavaCCを使ったので、演算子順位文法は記述できないようです。JavaCCが採用している再帰下降法は、認識力は特別強くありませんが手書きが容易だし、自動生成でも比較的読みやすいコードに変換されます。アルゴリズムの基本は、読んだトークンに基づいて、どの構文規則のどの部分に進むかを判定します(若干の先読みはできます)。構文規則を左から右に見ていきながら、処理を進めます。
構文規則とプログラムの関係は:
| 構文 | プログラム |
|---|---|
| 連接 | 順次実行 |
| 選択 | ifまたはswitch |
| 繰り返し | while |
この再帰降下法で算術演算子(+, *, 単項-)の優先順位を表現するには、式を構成する加数(summand; 加法的因子)と因数(factor;乗法的因子)というサブ構文要素を導入して:
[追記 time="当日夕方"]あんれ!? ここから先の記述、なんか変だな。いま余裕がないから、明日直そう。[/追記]
[追記 date="翌日"]ここから先、確かに変なんだけど、直さないでそのまま保存しておきます。訂正は別エントリーにあります。[/追記]
式 ::= 加数 ('+' 加数)* // 式は加数の和
加数 ::= 因数 ('*' 因数)* | '-' 加数 // 加数は因数の積、または加数の符号反転
因数 ::= 数 | '(' 式 ')' // 因数は数、または式を括弧で囲んだ形
あるいは:
式 ::= 加数 | 加数 '+' 式
加数 ::= 因数 | 因数 '*' 加数 | '-' 加数
因数 ::= 数 | '(' 式 ')'
後者は、繰り返し(正規表現の'*')の代わりに、右再帰で表現したものです。プログラム的には、whileループの代わりに末尾再帰を使用ってことですね。個人的には、右再帰のほうが美しく感じます。*1
単項のマイナスがあるので、3 + - 5 * - - 3 * 5 + 2 のような多少違和感のある式も正しいことになり、これも一意的にパーズ(解析)できます。('+'も'*'も右結合的となる。)
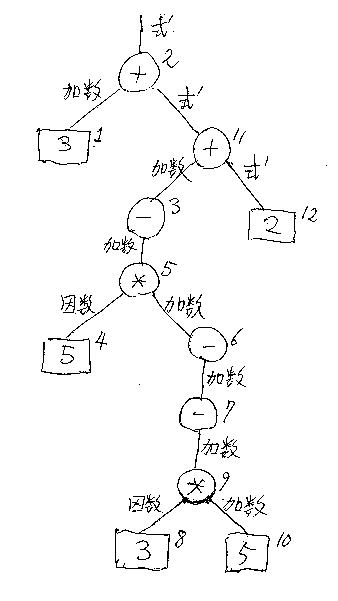
[追記]もっとツリーらしく描き直してみました。丸は演算子、四角は数です。丸/四角に添えてある番号は、式のなかでの(トークンとしての)出現位置です。
/* もっとツリーらしく描き直すとわかりやすいよ */+( //式
3, //数→因数→加数
+( //式
-( //加数
*( //加数
5, //数→因数
-( //加数
-( //加数
*( //加数
3, //数→因数
5 //数→因数→加数
)
)
)
)
),
2 //数→因数→加数→式
)
)
- 訂正はコチラ。