トラックバックをあらためて眺めていたら、co-scheさんの「海馬増設! ―はてなはじめました。―」に曰く:
id:m-hiyamaさんに憧れ、Hatena::Diaryに増設。
ダハハハ、持ち上げられてうれしいけど、背中がムズムズするよ。
それはともかく、co-scheさんの「感嘆した話。 ―配列への循環アクセス―」というエントリーに、循環的に配列を何度もなめながら何かするコードが話題になっていました。
例えば次のような感じです。
var MAX = 20;
a = ["Hello", "Yay", "Good job", "Bye-bye"];
size = a.length;
var next = 0;
for (var i = 0; i < MAX; i++) {
// print() -- Rhino's console output
print("(" + i + ")" + a[next]);
next = (next + 1) % size;
}
ポイントは、インデックスをインクリメントするとき、(next + 1) % size という計算をしているところです。これで、配列の終わりから先頭に戻るので、グルリングルリンと繰り返し配列をなめ回す処理ができます。
以下、このような循環に関連する話をいくつか、思いつくままに。
内容:
- 螺旋階段を昇るアイの影は、時計の針のように動く
- えっ!? 普通の整数も時計のように回っていたのぉ
- 6時で昼から夜に切り替わる:2の補数表現
- 角度の計算には引き算が不要
- いっぱいになったらごめんなさい:リングバッファ
螺旋階段を昇るアイの影は、時計の針のように動く
先のプログラムの変数iと変数nextの動きを追っていくと:
| 変数i | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ... |
|---|---|
| 変数next | 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, ... |
iをMAXで止めたのは実際上の事情に過ぎず、止まらなくていいならiはいくらでも順に増えます。一方のnextは、0, 1, 2, 3 を繰り返します。iは直線上を走り、nextは円環(輪っこ)上を回る感じですね。この状況を絵に描いてみました。
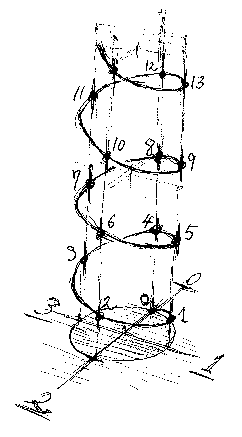
実は同じ絵を「代数系と準同型写像の絵を描いてみました」でも描いたのだけど、ひどくデッサンが狂っていたので描き直したよー*1。変数iが走る直線をグリグリねじって螺旋階段にしたわけ。螺旋階段を昇るiの影が地面に落ちると、影=変数nextは「15分おき目盛り付き時計の針」のように回りますね。
せっかくだから(?)、本物の螺旋階段(鉄創庵さん:http://www.tessoan.com/cate1/03/7_12/tenjin.html より):

えっ!? 普通の整数も時計のように回っていたのぉ
co-scheさん曰く:
これだと[檜山注:currentIndex++を続けると]いつかはcurrentIndexがNumber.MAX_VALUEに達してしまいます。
JavaScriptのNumber.MAX_VLUE(1.7976931348623157e+308)は、1を足してももう増えずに同じ値にとどまるみたいですね。もっとも、そこまで行く前に整数として正確な表現はできなくなります。絶対値が2の53乗までは「整数としての正確さ」が保証されているようです。
と、JavaScriptは「あんまり大きな数はダメー」という態度ですが、次のCプログラムはどうなるでしょう?
#includemain(int argc, char** argv) { int i; unsigned char u; for (i = 0, u = 0; i < 300; i++) { printf("%d\n", u++); } }
uが大きくなると、平気でゼロにラップアラウンドします。出力はこんな感じです。
0 1 2 3 ... (省略) 253 254 255 0 ←注目 1 2 3 ... (省略) 41 42 43
つまり、0から255までの目盛りが付いている時計の針のように動くわけね。
6時で昼から夜に切り替わる:2の補数表現
それでは、符号付き8ビット整数(Cのsigned char)ならどうでしょうか?
#includemain(int argc, char** argv) { int i; signed char s; for (i = 0, s = 0; i < 300; i++) { printf("%d\n", s++); } }
こんなです。
0 1 2 3 ... (省略) 125 126 127 -128 ←注目 -127 -126 ... (省略) -3 -2 -1 0 ←注目 1 2 3 ... (省略) 41 42 43
普通の時計の6時のところで、「正の大きな数」から「負の(絶対値が)大きな数」に切り替わるのですね。6時より右側半円弧が正、6時より左側半円弧が負と使い分けます。
現在の多くのコンピュータは、この方式で負の数を表します。「2の補数表現」と呼んだりします。
角度の計算には引き算が不要
8ビット整数だと、全部で256個しかないので、時計の文字盤に整数を刻んでも目盛りを判別できるでしょう。しかし、32ビット整数は43億個くらいあります。43億の目盛りは刻みきれないでしょうね。それで、整数(離散量)じゃなくて連続量と考えてしまいましょう。
丸い輪に連続的な目盛りといえば、そうです、分度器ですね。まー、目盛りは離散的だけど、角度は連続量ですよ。角度というのは、パイの形(扇形)の丸い部分の長さですから、長さ同様に足し算、引き算ができます。ただし360度(弧度法では2π)を超えたら360度で割った余りを使うので、時計の計算と同じです。
さて、「2の補数表現」のメリットとして、引き算と足し算を区別しなくてすむことがあります。これはどういうことか? 角度の計算で見てみましょう。
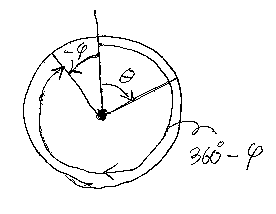
θとφという2つの角度があったとして、θ - φ という引き算をしましょう。絵では 0 < φ < θ となってますが、以下の議論は符号や大きさに関係しません。引き算 θ - φ は、θ + (-φ) とも考えられるので、反時計回りの -φ が描いてあります。その -φ ですが、時計回りに計れば、360°- φ (弧度法では 2π - φ) と同じですよね。
いま、思い切って、θ と 360°- φ を足し算してみます。
θ + (360°- φ) = 360°+ θ - φ = 360°+ (θ - φ)
角度は、360°(一回転分)を足しても変わらないので、360°+ (θ - φ) = θ - φ です。引き算をするのに、足し算だけで出来ちゃいましたよ。
なんかインチキくさい? θ - φ の代わりに θ + (360°- φ) をしているけど、360°- φ と前もって引き算してるじゃねーか。いやっ、360°- φ は -φ のことなんで、単に符号反転しているだけです。正確に言えば、「引き算をするのに、符号反転と足し算だけで出来る」ですね。幸いなことに、コンピュータにとって符号反転はさほどの手間じゃありません(全ビットを反転させてから1を足す)。引き算回路が不要になってラッキー。
いっぱいになったらごめんなさい:リングバッファ
(next + 1) % size の応用として、リングバッファを書いてみましょう。リングバッファの実装は、配列を循環的に使います。先入れ先出し(FIFO)なのでキュー(待ち行列)の一種です。バッファがいっぱいになると、それ以上はデータを入れません。空きが出来ればまた入れるようになります。
以下のJavaScriptコードでは:
- isAlmostFull(1つ分しか空いてない)と、もう「ごめんなさい」します。このほうが簡単に書けるので。
- isAlmostFullの状態でpost(データの追加)しても、黙ってデータが捨てられます。
- isEmptyの状態でfetch(データの取得)するとエラーになります。
/* RingBuffer.js */
function RingBuffer(size) {
if (size < 2) {
throw "Too small buffer size";
}
this.size = size;
this.buffer = new Array(size);
this.base = this.next = 0;
}
RingBuffer.prototype.isEmpty = function() {
return this.next == this.base;
};
RingBuffer.prototype.isAlmostFull = function() {
return (this.next + 1) % this.size == this.base;
};
RingBuffer.prototype.post = function(item) {
if (this.isAlmostFull()) {
return; // do nothing;
}
this.buffer[this.next] = item;
this.next = (this.next + 1) % this.size;
};
RingBuffer.prototype.fetch = function() {
if (this.isEmpty()) {
throw "Buffer is empty";
}
var item = this.buffer[this.base];
this.base = (this.base + 1) % this.size;
return item;
};
RingBuffer.prototype.clear = function() {
this.base = this.next = 0;
};
RingBuffer.prototype._dump = function() {
// for debug
var s = "[" + this.buffer.toString() + "]";
print(s); // Rhino only
};
*1:つっても、これもなんかズレてる感じだけど。