ホッピングボール・マシンの話は、ぼちぼち、ゆるゆる、順不同でいきたいと思います。できれば一話完結の説明にしたいと思いますが、毎回予備知識ゼロからの説明はさすがに無理かもな。
んで今日だけど、「引き算はなくてもだいたい大丈夫」に、「足し算で作り出せる数」がホッピングボール・マシンに関係する、と書いたので、このことを取り上げます。
内容:
- 有向グラフのサイクル
- 素サイクルをくっつけたホッピングボール・マシン
- 観測データによって、どこまで区別できるか
- 区別できないことは悪いことか
●有向グラフのサイクル
ホッピングボール・マシンの内部は有向グラフになっています。グラフ理論からの言葉を1つだけ導入しておきます -- それはサイクル(閉路、輪体)です。サイクルとは、あるノード(頂点)から出発して同じノードに戻る運動の跡<あと>のことです。運動とは、辺に沿ってノードを渡り歩くことです。辺(矢印)と逆向きには移動できません。
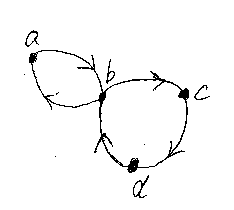
例えば上の図で、a→b→a→b→c→d→b→a はサイクルです。このサイクルは、同じノード(例えばb)を何度も通過してます。各ノードを1回しか通過しないサイクルは素サイクルと呼びましょう。a→b→a、b→c→d→b は素サイクルです。サイクルでは、運動の出発点=到着点ですが、この点(ノード)を基点ノード、あるいは単に基点と呼びます。ただし、基点を問題にしないときもあって、そのときは、a→b→a と b→a→b は同じサイクルとみなします。
いま定義した素サイクルだけをサイクルと呼ぶこともあります*1。また、基点を考えるか考えないかも状況によりけりです。ここでは、単にサイクルと言ったら、素サイクルとは限らない一般のサイクルです。たいてい基点を考えますが、文脈でわかるときはイチイチ基点を指定はしません。
誤解がないようにさらに2つの注意:
ループは、始点と終点が同じノードである辺のことです。ノードaから出るループは a→a というサイクルですが、ループとサイクルは別な概念ですから注意してください。(ただし、グラフ理論以外の分野では、ループとサイクルの区別をたいしてしないこともあります。)
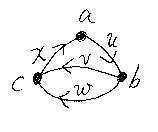
下の図のようなグラフでは、a→b→c→a と書いただけではサイクルを特定できません。bからcに至る辺が2本あるからです。このときは、a-(u)→b-(v)→c-(x)→a とか、a-(u)→b-(w)→c-(x)→a のように書くべきでしょう。しかし、2つのノードを結ぶ同方向の辺がたかだか1本であれば、a→b→c→a のような書き方で十分です。しばらくは、多重辺(2つのノードを結ぶ同方向の辺が複数)を考えないので、a→b→c→a のような書き方を使います。
●素サイクルをくっつけたホッピングボール・マシン
いくつかの素サイクルを、基点でくっつけた形のグラフを考えます。そのようなグラフを内部に持つホッピングボール・マシンを扱いましょう。入り口穴から入ったボールは基点に落ち、基点から出口穴に飛び出すとします。以下のA、B,Cはこのタイプのホッピングボール・マシンの例です。
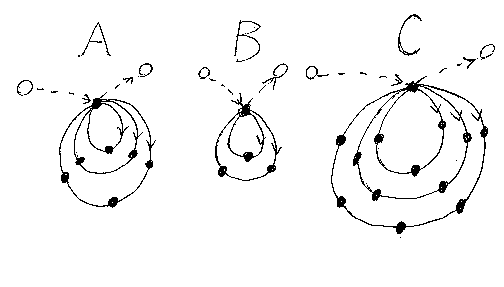
入り口と出口はそれぞれ1つなので、ボールを入れてから何秒後に飛び出すか、その秒数だけを観察・記録(それが試行)すればいいですね。何度も試行を繰り返すと、観測データとして秒数の集合が得られます。何回くらい試行すればいいでしょうか? 無限回です :-) 無限回試行すれば、完璧な観測データが得られます。人間は無限回の試行ができないって? じゃあ、超越的能力を持つ神様をアルバイトに雇って観察・記録させてください。
ホッピングボール・マシンの内部構造を知っているなら、実際の観察・記録をしなくても、観測データの予測ができます。ホッピングボール・マシンAに関して言えば、3つの素サイクルをまわるには、それぞれ2秒、3秒、4秒かかります。素サイクルをまったくまわらない場合も入れると、内部を動きまわっている時間は次のようになるでしょう。
- 0秒, 2秒, 3秒, 4秒, 5秒, 6秒, 7秒, 8秒, ...
秒数の列は、正の整数 2, 3, 4 から足し算で得られます。集合{2, 3, 4}から繰り返しを許して何個か(0個でもよい)の数を取り出して、それらを全部足します。そうやって得られた数達が、ホッピングボール・マシンAの観測データを構成します。
●観測データによって、どこまで区別できるか
ホッピングボール・マシンAとBは、内部構造が違います(見てのとおり)。しかし、観測データからAとBを区別することはできません。Aにおいて長さ4の素サイクルを1回まわる動作と、Bにおいて長さ2の素サイクルを2回まわる動作は、外からは区別できません。どちらの動作も4秒ですから、観測結果に違いは現れないのです。
一方、BとCは観測データから区別できます。
- Bの観測データ:0, 2, 3, 4, 5, 6, 7, 8, ...
- Cの観測データ:0, 4, 5, 6, 8, 9, 10, 11, ...
2, 3, 7 は、Bの観測データには含まれますが、Cの観測データには含まれません。BとCは明らかに違ったマシンだとわかります。
しかし、観測デーアの先のほう、大きな数のほうだけを見ると、BとCの区別もわからなくなります。比較的小さな数(短い秒数)のデータを切り落とされてしまうと、BとCは同じに見えちゃうんです。
この事実の背後にあるのが「引き算はなくてもだいたい大丈夫」に書いたことです。少し一般化した形でもう一度述べておくと:n個の正整数 a1, a2, ..., an に対して、N ≧ 0 があって*2、次の2つの集合は一致する。
- { x | x ≧N で、xは、a1, a2, ..., anと足し算だけで作り出せる}
- { x | x ≧N で、xは、a1, a2, ..., anと足し算/引き算で作り出せる}
上記、整数の性質については、MarriageTheoremさんやささはらさんが証明を与えてくれてます。いずれ、まとめる機会があるかもしれません。
ところで、{ x | xは、a1, a2, ..., anと足し算/引き算で作り出せる} という集合はよくわかっていて、a1, a2, ..., anの最大公約数の倍数集合です(これも、できればそのうち書く)。よって、素サイクルをくっつけたホッピングボール・マシンの観測データ、その先のほうだけを眺めると、一定間隔(1かも知れない)で数が並んでいることになります。
●区別できないことは悪いことか
ホッピングボール・マシンの観測データ(非負整数の並び)の、小さい数のほうが精度の高い情報を持っています。大きな数のほうでは、元のマシンの違いが消えてしまいます。となると、元マシンをできるだけ区別したいなら、小さい数のデータを調べたほうがよいでしょう。しかし、おおざっぱな分類をしたいなら、むしろ大きな数のほうに注目するのもテです。
観測データの(小さな数を無視した)大きな数のパターンは、ホッピングボール・マシンのとある種別に共通の特徴を表現していると期待できます。実際、一般のホッピングボール・マシンのサイクルに関する基本情報は、大きな数のパターンから抽出できます。
と、内部構造を限定した上で、観測データから分かることを少し調べてみました。一般のホッピングボール・マシンを調べるときも、今回述べたような、出入り口が1つずつのマシンの観測データが基本となります。こういった具体的で細々した解析と、アブストラクトナンセンスなマシナリーの両方を使って、ホッピングボール・マシンを調べていきたいと思います。