ホモトピー同値は何故重要なんだろう - 檜山正幸のキマイラ飼育記 (はてなBlog)

「ホモトピー・ナントカ」という記事を書いてはみたのですが、ホモトピーわかりませーん。でも、これはやっぱり大事そうだな、という感触はあります。型理論への応用で注目されているようですが、状態遷移や模倣の議論でもホモトピー的発想は有効そうな感じがします。「感じ」だけど。

「同じ」をゆるめる

ホモトピー的発想でモノを見ることは、「同じ」という概念をゆるめることでしょう。「同じである」を基本とする代わりに、「同じようなものだ」とか「だいたい同じだろう」を使って議論をすることですね。

圏のなかでの「対象の同型」という概念は「同じ／等しい」よりゆるい概念です。例えば、次の3つの図形を考えてみます。

{(x, y)∈R² | x² + y² = 1}
{(x, y, z)∈R³ | x² + y² = 1 かつ z = 0}
R/Z = R/〜 (x 〜 y ⇔ (x - y) が整数）

これらの図形の台（underlying set）は違う集合です。が、これらを区別して取り扱うのは生産的とは言えません。「同じようなものだ」とみなすための手段に、同型射（この場合は連続な双射）があります。同型射があるからこそ、対象の同型という概念が定義できます。

今例に出した3つの図形のどれか、あるいは3つの具体的図形を抽象した図形を「円周」と呼びます。円周の具体的な表現／作り方はいくらでもありますが、それらはどれも同じようなもので「円周」と呼んでいいのです。

次に、ソリッドトーラスを考えてみます。

{(x, y, z, w)∈R⁴ | x² + y² = 1 かつ z² + w² ≦ r}

円周をS¹、半径がrの円板をD(r)と書くとして、この図形・ソリッドトーラスは S¹×D(r) と書けます。rが正の数のとき、S¹と S¹×D(r) は同型になりませんから、同型の意味でも違う図形です。

しかし、rがものすごく小さい数のとき、S¹×D(r) と S¹ はほとんど同じに見えますよね。rがうんと小さい時と r = 0 の差はないように思えます。それにもかかわらず、図形の同型（位相空間と連続写像の圏の同型）では、r = 0 のときに急激な質的変化が起きます。なんか直感にあいません。

このことは、「次元なんて曖昧なんだよ」という記事でも取り上げました。

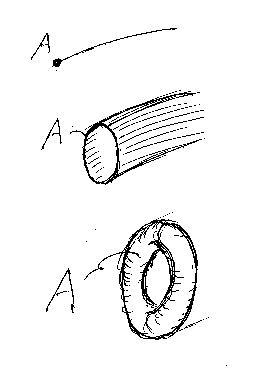
Aは線分の端で点（0次元）に見えた。が、近づいてみれば線分ではなくて管（チューブ）であり、端であるAも実は円周だった、ってのがまん中の絵です。もっと近づくと、円周じゃなくてドーナツ面（トーラス）だった、てのが最後の絵。

x² + y² = 1 で定義された円周をソリッドトーラスの芯に埋め込む写像 (x, y) |→ (x, y, 0, 0) を考えます。この写像はホモトピー同値写像です。ホモトピー同値写像があるなら、2つの図形はホモトピー同値です。対象のあいだのホモトピー同値の関係は、同型よりもっとゆるくなった「だいたい同じようなものだ」という関係です。

ホモトピー同値による分類は同型による分類よりもっと粗っぽくなります。精密さに欠けるとも言えますが、より大雑把に見たほうが扱いやすかったり、無駄な区別がなくなって本質が見えることもあります。同型による分類の無駄な精密さが邪魔なとき、よりゆるい分類（＝同値関係）を採用するのは良いアイディアです。

2 + 3 = 5 はホモトピー同値

ホモトピー同値は図形の分類法なのかというと、図形に限定されるわけではありません。図形的な（位相的な）ホモトピーの圏論的な一般化／公理化として弱同値があります。弱同値の定義もいくつかのバージョンがありますが、同型射全体を含む弱同値射という射のクラスを備えた圏を考えるのは共通です。対象Aから対象Bへの弱同値射があれば、AとBは弱同値（あるいは単に同値）です。

弱同値射は同型射とは限りません。よって、弱同値射の逆があることは保証されません。しかし、仮想的な圏を想定して、その圏のなかでは弱同値射に逆があるとみなします。この仮想的な圏がもとの圏のホモトピー圏とか（弱同値射に関する）局所化と呼ばれる圏です。ホモトピー圏のなかでの逆は、擬逆と呼ばれます。つまり、弱同値射に逆は存在しないかも知れないが擬逆は存在します。

以上のような枠組みと考え方は、状態遷移系や項書換え系などでも使えそうです。もっと素朴な“計算”においても弱同値や擬逆は登場します。例えば、2 + 3 = 5 という等式を素朴に解釈してみると、イコールは弱同値のように思えます。

僕自身の経験からも、うちの子供達の様子を見ても、小学校のはじめの頃の「=」は、左に“問題の式”、右に“答の値”を書く習慣になっています。左から右への変形、あるいは項書換えが行われるわけです。書き換えの方向性を強調して 2 + 3 ⇒ 5 と書きましょう。

「⇒」を算術式のあいだの射と考えると、2 + 3 ⇒ 5 の方向の射（計算行為）はあっても、5 ⇒ 2 + 3 という射はないのです。「5 = ? 」という問題を出しても子供は答えられない、つまり射を構成できない、構成できないモノはないのです。少なくとも、オリジナルの「小学校低学年の計算行為」の圏のなかでは 5 ⇒ 2 + 3 という射はありません。

“問題の式”と“答の値”は等しいのだ、と教えることは、計算行為の射を弱同値射とみなすことを指示します。2 + 3 ⇒ 5 という弱同値射の存在から 5 ⇒ 2 + 3 という擬逆の存在を想定することになります。計算行為を射とする圏を考えて、すべての射を弱同値射とみなして作ったホモトピー圏は、値（計算結果）の等値性を射とする圏となります。

この簡単な例からも、ホモトピー同値が計算の基本部分に関わることがうかがわれます。