以下の過去記事達で属性付きn-グラフ(主に n = 0, 1, 2)について述べました。
この記事では、グラフ〈有向グラフ〉を半グラフ〈無向半グラフ〉に置き換えて、属性付き半グラフについて述べます。属性付けは、原理的にはグラフでも半グラフでも変わらないのですが、半グラフになるとグラフより複雑になります。
標準的〈standard〉な属性についてもこの記事で述べます。$`\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\mbf}[1]{\mathbf{#1}}
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\msc}[1]{\mathscr{#1}}
%\newcommand{\mbb}[1]{\mathbb{#1}}
\newcommand{\In}{\text{ in }}
\newcommand{\H}{\text{-}}
%\newcommand{\msc}[1]{\mathscr{#1}}
%\newcommand{\mbb}[1]{\mathbb{#1}}
\newcommand{\In}{\text{ in }}
%\newcommand{\twoto}{\Rightarrow }
%\newcommand{\op}{\mathrm{op} }
\newcommand{\id}{\mathrm{id}}
%\newcommand{\u}[1]{\underline{#1}}
%\newcommand{\o}[1]{\overline{#1}}
\newcommand{\T}[1]{\text{#1}}
\newcommand{\hyp}{ \text{-} }
%\newcommand{\Iff}{ \Leftrightarrow }
\newcommand{\Imp}{ \Rightarrow }
\newcommand{\parto}{\supset\!\to}
`$
内容:
半グラフについて
以下の過去記事で半グラフについて説明しています*1。
特に端的に「半グラフとは何か」が書いてある部分は:
上記の2つの記事では、ハックニーの論文 Categories of graphs for operadic structures から引用した次の絵を参照しながら説明しています。
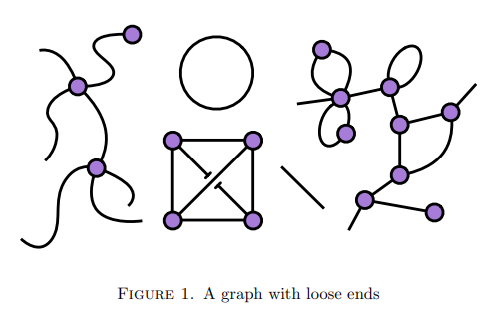
通常のグラフとは違い、半グラフ(辺の向きはない)では、端点〈ends〉を持たない辺を認めます。辺に対する端点の個数とループか否かで分類すると:
| 端点の個数 | ループか? | 呼び名 |
|---|---|---|
| 2 | No | 内部辺 |
| 1 | Yes | 自己ループ辺 |
| 1 | No | 境界辺〈外部辺〉 |
| 0 | No | 例外辺 |
| 0 | Yes | 例外ループ |
自己ループ辺は「端点が2個あるんだが、たまたま一致している内部辺の一種」とみなすのが普通です。内部辺だけを「辺」と呼ぶ人がいます(たぶん多数派)。僕は内部辺と境界辺〈外部辺〉をあわせて「辺」と呼称しています。
半グラフの辺は、“半分にした辺”がカップリング(くっついてひとつになる)*2して生じたとみなします。“半分にした辺”はフラグ〈flag〉と呼びます。
境界辺は、一本のフラグだけで(カップリングなしで)構成されるとみなします。ただし、次節で述べるワイヤリング図の場合は、境界ワイヤーも二本のフラグのカップリングで作られます。
半グラフ関連の呼び名は人により違い、山のような同義語があります。たとえば、フラグは branch〈枝〉、half edge〈半辺〉、 dart〈ダート〉などとも呼び、境界辺〈外部辺〉は open edge〈開放辺〉、loos edge〈ルーズ辺〉、dangling edge〈ぶら下がり辺〉、tail〈テール | 尾〉、leg〈脚〉、hair〈ヘア〉、lead〈リード〉、external flag〈外部フラグ〉、external line〈外線〉などとも呼びます。人、場面による違いがあっても、同義語です。
半グラフ vs. ワイヤリング図
ワイヤリング図はストリング図テンプレートの同義語です(「有限コレクションとスケマティックなシステム記述 // ワイヤリング図達の複圏」参照)。ストリング図テンプレートとストリング図を区別しないこともあるので、結果的に、ワイヤリング図、ストリング図テンプレート、ストリング図はあまり区別されません。
半グラフとワイヤリング図もほぼ同じです。違いは:
- 半グラフは、特にことわりがなければ辺に向きはないが、ワイヤリング図は原則的にワイヤーに向きがある。
- 半グラフでは、ワイヤリング図の境界ボックス〈外部ボックス〉に相当するものは考えない。ただし、ワイヤリング図でも境界ボックス〈外部ボックス〉を考えないこともある。
- 半グラフでは、特にことわりがなければ修飾(後述)はないが、ワイヤリング図は最初から修飾を考えていることが多い。
用語法の対応は次のようです。
| 半グラフ | ワイヤリング図 |
|---|---|
| 頂点 | ボックス |
| フラグ | ポート |
| 辺 | ワイヤー |
| 例外辺 | ベアワイヤー〈bare wire〉 |
| 例外ループ | サークル(使用を非推奨) |
| パートナー指定対合 | ワイヤリング対合 |
| 境界写像 | 所属写像 |
| (無し) | 境界ボックス〈{外部 | キャンバス}ボックス〉 |
「サークル」が非推奨なのは、ワイヤリング図を絵に描いたときの“ボックスの境界”(境界ボックスではない)をサークルと呼ぶことがあるからです。「境界ボックスのボックス境界」より「境界サークル〈外部サークル〉」が簡潔です。なお、「ノード」は、半グラフでもワイヤリング図でも共通に使えます。
半グラフの定義
半グラフの定義は「半グラフの様々な定義」に色々紹介しています。「強化ファインマン・グラフとバタニン/バーガー半グラフ」に、さらに追加の定義が書いてあります。
色々ある、あり過ぎるのが問題です。現時点で、ひとつだけ選べと言われれば、ボリソフ/マニンの定義を選びます。が、ボリソフ/マニンの定義では、例外辺と例外ループが扱えません。ダンクソ/ハラーチェバ/ロバーツォン(Circuit algebras are wheeled props)は、ボリソフ/マニンの定義を手直ししてますが、あまり使いやすくありません。ここでは、ダンクソ/ハラーチェバ/ロバーツォンとは別な(ボリソフ/マニン流への)補正案を紹介します。
「属性付き2-グラフのスノーグローブ現象」で述べたように、グラフや半グラフの定義には、その定義手段〈defining device〉としてグラフを使います。「グラフの定義にグラフを使う」というメタ巡回〈メタ循環 | meta-circlular〉構造が現れます。これはややこしくて混乱しがちなんですが、そういうもんだと諦めるしかないです。
グラフ〈有向グラフ〉を定義する形状グラフは簡単です。
$`\quad \xymatrix{
\cdot \ar@/^/[r] \ar@/_/[r]
&\cdot
}`$
上記のグラフのドット($`\cdot`$)のところに集合を、矢印のところに写像〈関数〉を割り当てると、それでひとつのグラフ〈有向グラフ〉になります。割り当てる集合や写像に条件はありません。場合により「有限集合に限る」のような条件をつけるときもあるでしょうが。
半グラフ〈無向半グラフ〉を定義する形状グラフは複雑になります。しかも、矢印に割り当てる写像には条件が付きます(後述)。半グラフのための形状グラフは以下のようです。ドットが5個(4個ではない)あるのに注意してください。
$`\quad \xymatrix{
\cdot \ar@(ul, dl)[0,0] \ar[dr]
\\
\cdot \ar@(ul, dl)[0,0] \ar[r]
& \cdot
\\
\cdot \ar@(ul, dl)[0,0]
\\
\cdot
}`$
ドットと矢印に名前〈一意識別子〉を付けないと、それについて語ることが出来ないので名前を付けます。
$`\quad \xymatrix{
*{F_1} \ar@(ul, dl)[0,0]_{\iota_1} \ar[dr]^{\beta_1}
\\
*{F_2} \ar@(ul, dl)[0,0]_{\iota_2} \ar[r]_{\beta_2}
& V
\\
*{F_3} \ar@(ul, dl)[0,0]_{\iota_3}
\\
L
}`$
この時点での名前は単なるID〈一意識別子〉で、集合や写像を表わすわけではありません。この形状グラフに、具体的な集合・写像を割り当てると実際の半グラフができます。半グラフの名前を $`A`$ とすると、$`A`$ を集合圏 $`\mbf{Set}`$ 内で見ると、次の図式になります。
$`\quad \xymatrix{
*{A(F_1)} \ar@(ul, dl)[0,0]_{A(\iota_1)} \ar[dr]^{A(\beta_1)}
\\
*{A(F_2)} \ar@(ul, dl)[0,0]_{A(\iota_2)} \ar[r]_{A(\beta_2)}
& A(V)
\\
*{A(F_3)} \ar@(ul, dl)[0,0]_{A(\iota_3)}
\\
A(L)
}\\
\quad \In \mbf{Set}
`$
以下では、集合は「有限集合に限る」という条件を付けます。つまり、有限半グラフだけ考えます。
習慣により、$`A(V)`$ は $`V(A)`$ と書き、$`A(\beta_2)`$ は $`{\beta_2}_A`$ と書く、なんてことになります。さらに、3つの $`\beta_1, \beta_2, \beta_3`$ は名前をオーバーロードして、すべて $`\beta`$ として、$`{\beta_2}_A`$ は $`\beta_A`$ でよい、とかの規則も導入します。書くのが楽になりますが、略記規則でわけわかんなくなる弊害もあります。とはいいながら、ここでもオーバーロード・略記・同一視はしますけどね。
半グラフ $`A`$ を有限集合圏内に展開した図の現実的妥協バージョンは次のようです。
$`\quad \xymatrix{
*{F_\mrm{bd}(A)} \ar@(ul, dl)[0,0]_{\id} \ar[dr]^{\beta_A}
\\
*{F_\mrm{in}(A)} \ar@(ul, dl)[0,0]_{\iota_A} \ar[r]_{\beta_A}
& V(A)
\\
*{F_\mrm{ex}(A)} \ar@(ul, dl)[0,0]_{\iota_A}
\\
{L_\mrm{ex}(A)}
}\\
\quad \In \mbf{FinSet}
`$
以下のように読みます。
- $`F_\mrm{bd}(A)`$ は、グラフ $`A`$ の境界辺を構成する境界フラグ〈boundary Flag〉達の有限集合である。
- $`F_\mrm{in}(A)`$ は、グラフ $`A`$ の内部辺を構成する内部フラグ〈internal Flag〉達の有限集合である。
- $`F_\mrm{ex}(A)`$ は、グラフ $`A`$ の例外辺を構成する例外フラグ〈exceptional Flag〉達の有限集合である。
- $`L_\mrm{ex}(A)`$ は、グラフ $`A`$ の例外ループ〈exceptional Loop〉達の有限集合である。
- $`V(A)`$ は、グラフ $`A`$ の頂点〈Vertex〉達の有限集合である。
- $`\id : F_\mrm{bd}(A)\to F_\mrm{bd}(A) \In \mbf{FinSet}`$ は、グラフ $`A`$ のパートナー指定対合の、境界フラグへの制限である。これは恒等写像である。
- $`\iota : F_\mrm{in}(A)\to F_\mrm{in}(A) \In \mbf{FinSet}`$ は、グラフ $`A`$ のパートナー指定対合(対合は involution)の、内部フラグへの制限である。
- $`\iota : F_\mrm{ex}(A)\to F_\mrm{ex}(A) \In \mbf{FinSet}`$ は、グラフ $`A`$ のパートナー指定対合(対合は involution)の、例外フラグへの制限である。
- $`\beta : F_\mrm{bd}(A)\to V(A) \In \mbf{FinSet}`$ は、境界写像〈boundary map〉の、境界フラグへの制限である。
- $`\beta : F_\mrm{in}(A)\to V(A) \In \mbf{FinSet}`$ は、境界写像〈boundary map〉の、内部フラグへの制限である。
パートナー指定対合 $`\iota`$ でカップリング(あるいはマッチング)された2本のフラグが一本の辺を形成します。境界フラグは、自分自身とカップリングされます。例外辺は、2本の例外フラグのカップリングの結果とみなします。境界フラグと内部フラグは1個だけ端点(である頂点)を持ち、それは境界写像 $`\beta`$ で指定されます。例外フラグに端点はありません。例外ループは、独立した集合 $`L_\mrm{ex}(A)`$ にまとめておきます。
半グラフの構成素として出現する有限集合が空であることを禁止しません。例えば、$`V(A)`$ が空なら、半グラフ $`A`$ は例外辺と例外ループだけで構成されます。例外フラグ達の集合も例外ループ達の集合も空なら、$`A`$ は空半グラフ〈empty semi-graph〉です。
パートナー指定対合 $`\iota_A`$ は対合なので、次の条件を課します。
$`\quad \iota_A ; \iota_A= \id`$
$`F_\mrm{in}(A), F_\mrm{ex}(A)`$ 上の $`\iota_A`$ は不動点を持たない、という条件も課します。
属性とは
属性付き半グラフを考えるのですが、属性とは何でしょう。属性は、属性名で識別されます。属性名の指す実体は何でしょうか? これは部分関数です。
まず、部分関数は、集合圏内の次の図式で表現されます。
$`\quad \xymatrix{
{}
&D \ar@{_{(}->}[dl] \ar[dr]^f
&{}
\\
A
&{}
&B
}\\
\quad \In \mbf{Set}`$
ここで $`D\hookrightarrow A`$ は包含写像なので、$`D`$ は $`A`$ の部分集合です。この状況で、部分集合 $`D`$ を暗黙化して次のように略記します。
$`\quad f: A \parto B \In \mbf{Set}`$
$`f`$ は、包含写像を伴って部分関数〈partial function〉で、部分集合 $`D\subseteq A`$ は $`f`$ の定義域〈domain of definition〉です。部分関数 $`f`$ の定義域は $`\mrm{def}(f)`$ と書きます。
$`A`$ を半グラフとして、$`A`$ を構成する各種集合の直和を次のように書きます。
$`\quad \mrm{All}(A) := F_\mrm{bd}(A) + F_\mrm{in}(A) + F_\mrm{ex}(A) + V(A) + L_\mrm{ex}(A)
`$
$`\mrm{All}(A)`$ には、$`A`$ のすべての境界フラグ達、すべての内部フラグ達、すべての例外フラグ達、すべての頂点達、すべての例外ループ達が含まれています。
$`Y`$ を適当な集合として、半グラフ $`A`$ 上の$`Y`$-値属性〈$`Y`$-valued attribute〉、あるいは$`Y`$-ターゲット属性〈$`Y`$-targeted attribute〉とは、次のような部分関数です。
$`\quad f: \mrm{All}(A) \parto Y \In \mbf{Set}`$
$`\msc{G}`$ (筆記体ジー)が半グラフ達の集合(有限集合でも大きい集合でもかまわない)として、$`\msc{G}`$ の各要素に$`Y`$-値属性が割り当てられているとき、属性の族 $`(f_A)_{A\in \msc{G}}`$ を、$`Y`$-値の 多相属性〈polymorphic attribute〉、または汎用属性〈generic attribute〉と呼びます。
$`f`$ が、半グラフ達の集合 $`\msc{G}`$ 上の$`Y`$-値多相属性のとき、その成分〈component〉*3は次のような属性です。
$`\text{For }A\in \msc{G}\\
\quad f_A : \mrm{All}(A) \parto Y \In \mbf{Set}
`$
実際に属性が使われる場面では、多相属性が使われるときが多いので、多相属性〈汎用属性〉も単に属性と呼びます。
属性名と規約
属性(多くの場合は多相属性)は、名前で識別します。例えば、「属性付きn-グラフはいけてる // 予約属性と形状・図式・テンプレート」では、予約属性として $`\T{id}, \T{val}, \T{name}, \T{class}`$ という名前の属性を導入しています。予約と言っているのは、これらの名前の属性の使用法を事前に約束しておこう、ということです。
特定の名前の属性に対する使用法の約束を規約〈convention〉といいます。規約は自然言語によるゆるい約束事です。しかし、正確さを増すことはできます。例えば、「$`\T{id}`$ という名前の属性は一意識別子であるべし」という規約は以下のように言い換えられます。
$`\quad \forall A\in \msc{G}.\, {^\wedge\T{id}}_A \T{ is injective}
`$
ここで $`{^\wedge\T{id}}`$ は、$`\T{id}`$ という名前に対応する多相属性(部分関数達の族)だとします。多相属性の半グラフ $`A`$ での成分は、
$`\quad {^\wedge\T{id}}_A : \mrm{All}(A) \parto \mrm{cod}({^\wedge\T{id}}_A) \In\mbf{Set}`$
です。これが単射〈injective〉ということは、以下の写像が単射なことです。
$`\quad {^\wedge\T{id}}_A: \mrm{def}({^\wedge\T{id}}_A) \to \mrm{cod}({^\wedge\T{id}}_A) \In \mbf{Set}`$
この性質は、単一の半グラフに対して成立するのではなくて、半グラフ達の集合 $`\msc{G}`$ に属するすべての半グラフに対して成立します。
なお、$`\T{id}`$ という名前や、部分関数 $`{^\wedge\T{id}}_A`$ は、圏の恒等射とは何の関係もありません。たまたま名前の綴りがかぶってしまっただけです。こういった偶発的なかぶり〈コンフリクト〉で惑わされないように注意してください。
以上は、$`\T{id}`$ という名前の属性に対する規約を正確に述べた例です。$`\T{id}`$ という名前以外でも、規約を決めておくと便利です。次節で述べます。
標準的な属性
id属性
id属性は前節で例に出しました。id属性が満たすべき条件は、半グラフ $`A`$ の $`\mrm{All}(A)`$ 上の部分関数 $`{^\wedge\T{id}}_A`$ が単射なことでした。
val属性
val属性では、意味論的な値を割り当てます。何が「意味論的」かを一律に定義することはできないので、曖昧・インフォーマルな規約になります。
半グラフを圏論で使うときは、部分関数 $`{^\wedge\T{id}}_A`$ の余域は、適当な圏 $`\cat{C}`$ の対象集合 $`|\cat{C}|`$ や射集合 $`\mrm{Mor}(\cat{C})`$ です。
name属性
name属性は、val属性による値割り当てを制約します。次の条件を要求します。
$`\text{For }A\in \msc{G}\\
\quad \forall x, y\in \mrm{def}({^\wedge\T{val}}_A) \cap \mrm{def}({^\wedge\T{name}}_A).\, \\
\qquad {^\wedge\T{name}}_A(x) = {^\wedge\T{name}}_A(y) \Imp
{^\wedge\T{val}}_A(x) = {^\wedge\T{val}}_A(y)
`$
class属性
class属性の値は、val属性の余域の部分集合、または部分集合の名前です。class属性も、val属性による値割り当てを制約します。次の条件を要求します。
$`\text{For }A\in \msc{G}\\
\quad \forall x \in \mrm{def}({^\wedge\T{val}}_A) \cap \mrm{def}({^\wedge\T{class}}_A).\, {^\wedge\T{val}}_A(x) \in {^\wedge\T{class}}_A(x)
`$
num属性
num属性は、id属性のように要素を識別するだけでなくて、要素のあいだに全順序を入れたいときに使います。num属性(部分関数)の余域は $`\mbf{N}`$ です。他の属性(id属性やlabel属性)の余域に $`\mbf{N}`$ を使うのは何ら問題ないし、$`\mbf{N}`$ を余域に使っても全順序は一切使わないことも自由です。
num属性(部分関数)は単射である必要はありません。が、スコープ(次節で説明)ごとの単射性は要求されるでしょう。num属性の使用例は後で出てきます。
label属性
label属性(部分関数)は、ラベル達の集合〈set of labels〉と呼ばれる集合に値を取ります。「ラベル」が何であるかを一律に定義することはできないので、曖昧・インフォーマルな規約になります。
type属性
type属性(部分関数)は、タイプ〈型〉達の集合〈set of types〉と呼ばれる集合に値を取ります。「タイプ〈型〉」が何であるかを一律に定義することはできないので、曖昧・インフォーマルな規約になります。
label属性の値を制約する目的で使います。label属性(部分関数)の余域を $`L`$ 、type属性(部分関数)の余域を $`T`$ として、$`\tau : L \to T`$ という関数があるとして、次を要求します。
$`\text{For }A\in \msc{G}\\
\quad \forall x \in \mrm{def}({^\wedge\T{label}}_A) \cap \mrm{def}({^\wedge\T{type}}_A).\, \tau({^\wedge\T{label}}_A(x) ) = {^\wedge\T{type}}_A(x)
`$
スコープにおける一意性
id属性は、定義域において単射であることを要求しました。label属性などでは、定義域の範囲ごとに単射であることを要求することがあります。定義域の範囲をスコープと呼びます。スコープは、スコープにおける一意性の定義に使います。
$`A`$ を半グラフとして、$`\mrm{All}(A)`$ の部分集合 $`S\subseteq \mrm{All}(A)`$ をスコープ〈scope〉と呼びます。
半グラフ $`A`$ 上の属性(部分関数) $`f`$ が スコープ $`S`$ 上で一意〈unique〉とは、部分関数 $`f`$ の $`S`$ への制限
$`\quad f|_S : S \parto \mrm{cod}(f) \In \mbf{Set}`$
が単射部分関数になることです。
具体例として、「頂点の近傍ごとに一意なラベリング」という概念を考えてみます。半グラフ $`A`$ の内部フラグ達と境界フラグ達の集合 $`F_\mrm{in}(A) + F_\mrm{bd}(A)`$ 上で定義されたラベル属性(部分関数)$`{^\wedge\T{label}_A}`$ が近傍ごとに一意とは次を満たすことです。
$`\quad \forall v\in V(A).\, {^\wedge\T{label}_A}|_{{\beta_A}^{-1}(v)} \T{ is injective}`$
つまり、頂点 $`v\in V(A)`$ ごとにスコープ $`{\beta_A}^{-1}(v) \subseteq \mrm{All}(A)`$ が決まり、label属性が決めるラベリング関数 $`{^\wedge\T{label}_A}`$ がスコープごとに一意ということです。
半グラフに対する修飾
半グラフに対する修飾〈decoration〉という概念を定義するにはニ種類の方法があります。
- 修飾されたグラフ達が形成する圏を公理的に定義する。
- 半グラフに対する修飾方法・手段を具体的に定義する。
ボリソフ/マニン(Generalized operads and their inner cohomomorphisms)は、abstract decorated semi-graph (論文内では abstract labeled graph)達の圏を公理的に規定しています。
一方、バーガー/カウフマン(Trees, graphs and aggregates: a categorical perspective on combinatorial surface topology, geometry, and algebra)は、修飾関手〈decorating functor〉という関手を使って半グラフを修飾する手段を定義しています。
ここでは、属性を使って半グラフを修飾する方法を幾つか紹介します。
半グラフへの向き付け
$`\mbf{2}`$ は二元集合とします(2つの要素は何でもよい)。半グラフ $`A`$ の内部辺、境界辺、例外辺に向きを付けるには、$`\mbf{2}`$ を余域とするpol属性を使います。pol は polarity〈極性〉からです。記法を簡潔にするために、関数 $`{^\wedge\T{pol}}_A`$ を $`p`$ と書きます。
$`\quad p : F_\mrm{bd}(A)+ F_\mrm{in}(A) + F_\mrm{ex}(A) \to \mbf{2} \In\mbf{Set}`$
$`p`$ は次を満たす必要があります。
$`\text{For } x \in (F_\mrm{in}(A) + F_\mrm{ex}(A))\\
\quad p(x) \ne p(\iota(x))
`$
$`F_\mrm{bd}(A)`$ 上での $`p`$ の値には特に制限はないです。
$`p`$ による極性割り当てがなぜ辺の向きを定義するかは、$`\mbf{2} = \{+, -\}`$ として、電気のプラスマイナスで考えれば分かるでしょう。プラスからマイナスに流れる電流の向きが辺の向きを与えます。
半グラフへの頂点ごとの順序付け
半グラフ $`A`$ のすべての頂点に対して、頂点に接続しているフラグ達に全順序を与えます。全順序を付けるには、$`\mbf{N}`$ を余域とするnum属性を使います。記法を簡潔にするために、関数 $`{^\wedge\T{num}}_A`$ を $`n`$ と書きます。
$`\quad n : F_\mrm{bd}(A)+ F_\mrm{in}(A) \to \mbf{N} \In\mbf{Set}`$
$`n`$ は、頂点 $`v\in V(A)`$ が決めるスコープ $`\beta^{-1}(v)`$ ごとに単射であることを要求します。それだけでなくて、単射による像は $`\{1, \cdots, n\}`$ という形だとします。要するに自然数番号による順番が決まる、ということです。
半グラフへのラベル付け
先に挙げた「頂点の近傍ごとに一意なラベリング」です。ダンクソ/ハラーチェバ/ロバーツォン(Circuit algebras are wheeled props)がこのラベリングを使っています。ただし、例外フラグ達 $`F_\mrm{ex}(A)`$ と例外ループ達 $`L_\mrm{ex}(A)`$ にもスコープ(集合 $`F_\mrm{ex}(A)`$ と $`L_\mrm{ex}(A)`$)内で一意なラベルを付けます。ラベリング関数を $`\ell := {^\wedge\T{label}}_A`$ とすると:
$`\quad \ell : (F_\mrm{bd}(A)+ F_\mrm{in}(A)+ F_\mrm{ex}(A) + L_\mrm{ex}(A) )\to L \In\mbf{Set}`$
$`L = \mrm{cod}(\ell)`$ はラベル達の集合です。
この他にも、用途により様々なラベル付けがあります。異なるラベル付け方式は、半グラフ上に異なる構造を誘導します。
おわりに
半グラフは、グラフ〈有向グラフ〉に比べて複雑ですが、極めて豊かな構造と広い応用を持ちます。それに属性を加えれば、さらに応用範囲は広がります。属性の実体は、$`\mrm{All}(A)`$ 上の部分関数です。半グラフに対する修飾と呼ばれる追加構造は、ほとんどは属性(または幾つかの属性の組み合わせ)で表現できます。
属性付き半グラフを構文的対象物〈syntactic object〉と考えると、“属性付き半グラフ言語”に対する構文論と意味論を展開できます。関係データベースの圏論的記述、テンソルネットワーク、圏論的システム理論などはその事例です。他にも応用はある/増えるでしょう。
*1:網羅的なリストは「スケマティック系のハブ記事 // 半グラフ」参照。
*2:男女のカップリングは「カプ」と省略するようです。
*3:多相属性は特殊な自然変換と考えることができます。成分は自然変換の成分のことです。