モナド、双圏、変換手

モナドを、双圏の3-圏BICATの0-変換手〈0-transfor〉として解釈します。

内容：

モナドはモノイド？

以前、「モナドはモノイドだが、モノイドじゃない」という記事を書きました。「モナドは、自己関手圏のなかのモノイド対象である」という事実が重要なのは確かなんですが、それがモナド概念の本質ってわけでもないので、あまり過大に喧伝すべきではありません。

モナドがモノイドになるのは、「モナドは、自明2-圏から圏の2-圏への“関手”である」ことの帰結です。よって、2-圏のあいだの“関手”に目を向けると、モナドに関する理解が深まります。2-圏のあいだの“関手”は、3-圏の射〈1-射〉なので、その3-圏も意識する必要があります。

「“関手”」と引用符を付けたのは、次のような言葉が同義語として使われる可能性があるからです。

1. 2-圏のあいだの準同型射〈homomorphism〉： トム：レンスターの用語法、「高次圏： 用語法と文脈（主に2次元） // テキスト（教科書的資料）」参照。
2. 2-圏のあいだの疑関手〈pseudofunctor〉： 伝統的用語法
3. 2-圏のあいだの2-関手〈2-functor〉： 2-圏のあいだの対応だから「2-」を付ける。
4. 2-圏のあいだの1-射〈1-morphism〉： 2-圏達の3-圏の1-射だから。
5. 2-圏のあいだの1-関手〈1-morphism〉： 「関手」を「射」と同義で使う場合。
6. 2-圏のあいだの0-変換手〈0-transfor〉： 変換手の番号付けはそういうルール。「変換手〈transfor〉は要らないだろう」参照。

上記の“関手”概念（内容的には同一概念）は、モナドの定義としては制約が強すぎます。モナドに対応する“関手”は：

1. 2-圏のあいだの射〈morphism〉： トム：レンスターの用語法
2. 2-圏のあいだのラックス関手〈laxfunctor〉： 伝統的用語法
3. (その他の用語法は省略、「高次圏： 用語法と文脈（主に2次元）」参照。)

用語法がグッチャングッチャンなのが悩みの種ですが、適宜注意を促しながら説明します。

双圏の3-圏

3-圏について短く正確に説明するのは難しいので、とりあえず次のように考えてください。

1. 3-圏には、対象と射〈1-射〉以外に、2-射、3-射がある。
2. 2-射は2つの射〈1-射〉のあいだを繋ぎ、3-射は2つの2-射のあいだを繋ぐ。
3. 射〈1-射〉、2-射、3-射のあいだに、いい具合に結合〈composition〉が定義されている。
4. 恒等射以外に、恒等2-射、恒等3-射があり、結合に対して単位〈unit〉となっている。

3-圏の構成素（対象、射、2-射,、3-射）を絵に描くと次のような感じです。

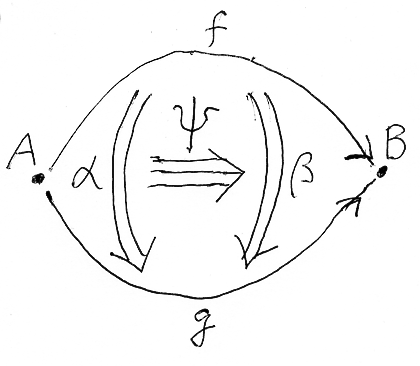
• A, B は対象
• f, g は射
• α, β は2-射
• Ψ は3-射

この絵は「圏論的宇宙と反転原理と次元付きの記法」に載せたものです。

3-圏には、“弱さ”によって様々なバラエティがありますが、単に「3-圏」と書いた場合には、“弱さ”を特定しない漠然とした意味で使います。“弱さ”については「高次圏： 複雑さの2つの方向と半厳密性」を参照してください。

次のように記号の約束をします。

• Cat ： 小さな圏を対象、関手を射、自然変換を2-射とする厳密2-圏
• s2-CAT ： 必ずしも小さくない厳密2-圏〈strict 2-category〉を対象、“関手”を射、“自然変換”を2-射、変更〈modification〉を3-射とする3-圏
• w2-CAT ： 必ずしも小さくない弱2-圏〈weak 2-category〉を対象、“関手”を射、“自然変換”を2-射、変更を3-射とする3-圏

「関手」と「自然変換」に引用符が付いているのは、前節で説明した事情です。後でより正確に定義します。

「弱2-圏」と「双圏」〈bicategory〉は同義語として使います（一切区別はしません）。同義語に対応して別名記号〈alias〉も使います。

• BICAT := w2-CAT

Catは厳密2-圏ですが、厳密2-圏は弱2-圏（a.k.a. 双圏）の特別なモノなので、次が成立します。

• Cat∈|BICAT|

圏（小圏）の2-圏Catについて議論する際に、外側の環境として3-圏BICATを使います。

モナドとは

モナドを定義する際に、外側の環境として3-圏 s2-CAT を使うことが多いです。この設定でのモナドに関しては次の記事で書いています。

• 最近のモナド論の概観と注意事項 1/2
• 最近のモナド論の概観と注意事項 2/2

s2-CAT を、w2-CAT = BICAT に置き換えることができます。一般性も複雑性も増しますが、大きく変わるわけではありません。ここでは、BICATを舞台（環境、世界）としてモナドを考えます。

K∈|BICAT|、つまり、Kは双圏とします。次のように約束します。

• Mnd(K) := (双圏K内のモナドの全体)

この定義(?)は非常に曖昧なものですが、すぐ後でより正確にします。太字でMndと書いたときは：

• Mnd := Mnd(Cat)

さて、Mnd(K) のより正確な定義とは次です。

• Mnd(K) := BICAT(₂I, K)

ここで、₂I は自明な2-圏、BICAT(-, -) は3-圏BICATのホム2-圏です。自明な2-圏とは、唯ひとつの対象と恒等射、恒等2-射しか持たない2-圏のことなので簡単です。であるなら、「3-圏BICATのホム2-圏」が分かれば Mnd(K) がハッキリすることになります。

双圏とラックス関手

「3-圏BICATのホム2-圏」という概念は、双圏と双圏の3-圏の理論のなかで定義されます。この分野のテキストは、「高次圏： 用語法と文脈（主に2次元） // テキスト（教科書的資料）」で紹介しています。トム・レンスターの極端に短い論説と、ヨーナス・ヒーデマンによる解題の書誌情報をコピーすると：

• Title: Basic Bicategories (1998)
• Author: Tom Leinster
• Pages: 11p
• URL: https://arxiv.org/abs/math/9810017

• Title: 2-Categories and Yoneda lemma (2017)
• Author: Jonas Hedman
• Pages: 76p
• URL: https://pdfs.semanticscholar.org/c54c/9106fd428ec7eaafa23dc33ae73928abfc67.pdf

エイドリアン・トシャー・ミランダの修士論文も同様な内容です。

• Title: Bicategories and Higher Categories (2017)
• Author: Adrian Toshar Miranda
• Pages: 64p
• URL: https://web.maths.unsw.edu.au/~danielch/thesis/adrian_miranda.pdf

チャンとした詳細な定義は、これらのテキストを参照してもらうことにして、大ざっぱな話と注意事項を続けることにします。

まず最初に注意すべきは、双圏の概念を確定しても BICAT が一意に決まるわけではないことです。BICATの射〈1-射〉の定義には様々なバリエーションがあります。このような多様性（と、それに伴う曖昧性）は高次圏論では常につきまといます。

BICATの射（双圏のあいだの“関手”）の種類として次の3種を考えることにします。

1. タイト関手
2. ラックス関手
3. 反ラックス関手

これらの“関手”については、「モナド論をヒントに圏論をする（弱2-圏の割と詳しい説明付き） // 圏論の用語法の問題点と対策」を参照してください。

BICATの射の選び方に応じて、次のように区別することにします。

1. BICAT^tight ： 射はタイト関手
2. BICAT^lax ： 射はラックス関手
3. BICAT^oplax ： 射は反ラックス関手

どれをデフォルトにするかは人により場合によりですが、ここでは（あくまでここでは）BICAT = BICAT^lax というデフォルト・ルールを採用します。理由は、BICAT^lax がモナドを定義する舞台として適切だからです*1。

次の記事は、モノイド圏（単対象双圏）のあいだのラックス関手が主題ですが、ラックス関手について扱っています。

• モノイド関手／ラックス・モノイド関手とその実例
• ラックス・モノイド関手について、もうちょっと

次の記事は、インデックス付き圏の拡張としてのラックス関手についてです。

• インデックス付き圏を拡張してファイバー付き圏へ

ラックス関手という概念は、通常の関手（1-圏のあいだの1-関手）とはだいぶ違います。2つの双圏のあいだの対応というよりは、2つの双圏をもとにして作られたモノイド類似代数構造と捉えたほうがいいでしょう。

3-圏のホム2-圏

圏の2-圏 Cat において、Cat(C, D) は単なる集合ではなくて圏になります。なので、Cat(C, D) はホム圏と呼ばれます。同様に、双圏の3-圏 BICAT において BICAT(K, L) は2-圏となり、ホム2-圏〈hom-2-category〉と呼ばれます。

BICAT(K, L) は2-圏なので、次のような構成素の集合があります。

1. Obj(BICAT(K, L)) = |BICAT(K, L)| = (対象の集合)
2. Mor(BICAT(K, L)) = (射〈1-射〉の集合)
3. 2-Mor(BICAT(K, L)) = (2-射の集合)

F, G:K→L を射（ラックス関手）、α, β::F⇒G:K→L を2-射〈自然変換〉とすると、ホムシング（ホム・ナントカのこと）は次のようになります。

1. BICAT(K, L) ： 3-圏 BICAT のホム2-圏
2. BICAT(K, L)(F, G) ： 2-圏 BICAT(K, L) のホム圏
3. BICAT(K, L)(F, G)(α, β) ： 圏〈1-圏〉BICAT(K, L)(F, G) のホムセット

Mnd(K) = BICAT(₂I, K) だったので、モナドの全体 Mnd(K) は3-圏のホム2-圏として定義されるのです。したがって、モナドの全体を理解するには、3-圏のホム2-圏を理解する必要があります。

関手と変換手

3-圏 BICAT のホム2-圏 BICAT(K, L) の対象集合 Obj(BICAT(K, L)) = |BICAT(K, L)| は、BICAT から見れば1-射の集合、つまりラックス関手の集合です。ラックス関手の集合を、Functor^lax(K, L) と書くことにすると：

• Functor^lax(K, L) = Obj(BICAT^lax(K, L))

laxがデフォルトなので外すと：

• Functor(K, L) = Obj(BICAT(K, L))

関手（この場合はラックス関手）を1-関手、自然変換を2-関手、変更を3-関手という言葉で表現するなら、次のように書けます。

1. 1-Functor(K, L) = Obj(BICAT(K, L))
2. 2-Functor(F, G:K→L) = Obj(BICAT(K, L)(F, G))
3. 3-Functor(α, β::F⇒G:K→L) = Obj(BICAT(K, L)(F, G)(α, β))

関手／自然変換／変更をひっくるめて k-関手 と呼べばいいんじゃないか、という話は次の記事にあります。

• 変換手〈transfor〉は要らないだろう

しかし、上記記事の追記に書いたような検索困難性と、伝統的な2-関手を1-関手と呼ぶことになるなどの欠点もあります。変換手〈transfor〉という言葉と、XFor という記号を使うなら：

1. 0-XFor(K, L) = Obj(BICAT(K, L))
2. 1-XFor(F, G:K→L) = Obj(BICAT(K, L)(F, G))
3. 2-XFor(α, β::F⇒G:K→L) = Obj(BICAT(K, L)(F, G)(α, β))

モナドは変換手の特別な場合になります。

1. ₂I→K in BICAT という0-変換手（1-射）がモナド
2. M⇒N:₂I→K in BICAT という1-変換手（2-射）がモナド射
3. α≡＞β:::M⇒N:₂I→K in BICAT という2-変換手（3-射）がモナド2-射

同じことですが：

1. Obj(Mnd(K)) = 0-XFor(₂I, K)
2. Mnd(K)(M, N) = 1-XFor(M, N:₂I→K)
3. Mnd(K)(M, N)(α, β) = 2-XFor(α, β::M⇒N:₂I→K)

BICATにおける番号付け〈次元〉と、Mnd(K) における番号付けがズレていることに注意してください。

現状においては、変換手という概念を用いてBICATの構造を整理するのが中庸として最適かも知れません。先に紹介したエイドリアン・トシャー・ミランダの論文は、変換手を使っています。一方、未整理で不整合が目立つ伝統的用語法については「高次圏： 用語法と文脈（主に2次元）」を参照してください。

図式の描き方

2-圏、3-圏の話では、大きめのペースティング図で記述と計算を行います。次は、エイドリアン・トシャー・ミランダの論文の、とあるページのスナップショットです。

「分かりやすさ」の感覚は人により違いますが、僕はペースティング図は苦手で、分かりにくいと感じます。同じ内容でもストリング図／ストライプ図で描くとずっと分かりやすく感じます。ストライプ図については、

• モノイド関手／ラックス・モノイド関手とその実例 // マッカーディのストライプ図

ストライプ図を使っている記事は：

1. モノイド圏と加群圏に関するフォークロアとマックレーン五角形・三角形
2. モノイド自然変換とモノイド同値関手
3. リストモナドとテンソル空間モナドのあいだの準同型射
4. インデックス付き圏を拡張してファイバー付き圏へ

ストリング図／ストライプ図を使うと、次の類似性が目視で確認できると思います。

線形代数	モナド	双圏の変換手
代数	モナド	0-変換手
加群	モナド射	1-変換手
加群射	モナド2-射	2-変換手

この類似性は、理解を容易にする効果がありますが、それだけでなく、背後にある大きな物語を示唆しているように思えます。

まとめ

• モナドの全体は、3-圏 BICAT のなかで定義できる。
• Mnd(K) = BICAT(₂I, K) である。
• ホム2-圏 BICAT(₂I, K) の構成素は、0-変換手, 1-変換手, 2-変換手である。
• モナド＝0-変換手、モナド射＝1-変換手、モナド2-射＝2-変換手
• （加群の）線形代数とモナドと（双圏の）変換手のあいだには類似性がある。

*1:[追記]「「モナド、双圏、変換手」への補遺」に書きましたが、このデフォルト・ルールは一般的ではなく、ときに不適切です。BICAT = BICAT^tight とするのが普通だと思います。[/追記]