このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

デカルト・タワーを求めて

雑記／備忘

マイクロコスモ原理、デカルト構造の無限タワーについて述べたことがあります（2018年）。

構造の無限タワーが存在するのは確実で、我々は無限先送り論法（逆帰納法）を使わざるを得ません。そして、実際に使っています。

最近書いた記事のなかでも、デカルト圏〈デカルト・モノイド圏〉に対するマイクロコスモ原理にちょっと触れました。一言でいえば*1：

あるいは、

環境としてのデカルト圏もデカルト圏なので、さらに外側（外側の外側）に環境としてのデカルト圏（環境としてのデカルト圏の環境としてのデカルト圏）が必要になります。この過程が無限に繰り返されます。

このような無限先送り論法をどうやって合理化するのか？ が、僕にとっての疑問・課題です。一年半前の時点よりは、その仕掛けが少しだけ分かった気がするので書いておきます。タイトルのデカルト・タワー〈Cartesian tower〉は、デカルト構造の無限タワーの意味です。下の画像は、ル・コルビュジエによって設計されたデカルト・スカイスクレーパー〈Cartesian skyscraper〉、名前が似てるだけ。

*2

内容：

圏の次元は上がらない

Ur （r = 0, 1, 2, ...）は宇宙〈グロタンディーク宇宙〉の無限系列とします（宇宙については、「階層的な圏論的宇宙・楽観的暫定版」参照）。

  • U0 ∈ U1 ∈ U2 ∈ ...

各UrはZFC類似集合論〈ZFC-like set theory〉のモデルで、その内部で集合論的構成（直積とかベキ集合とか）は問題なく出来るとします。Urに所属する集合を、階数rの小集合〈small set of rank r〉と呼びましょう。

階数rの小集合をベースにした、小集合の圏、小圏の圏を、

  • 0-Cat#r
  • 1-Cat#r

とします。今使った書き方は「高次圏： 複雑さの3つ目の方向と相対階数」、「階層的な圏論的宇宙・楽観的暫定版」で説明しています。0-Cat#r は1-圏であり、1-Cat#rは厳密2-圏になります。1-Cat#rの環境となる圏は、

  • 1-Cat#r ∈0 s2-Cat#(r+1)

ここで、'∈0' は「対象として含まれる」の意味で、1-Cat#r ∈|s2-Cat#(r+1)| と同じです。厳密2-圏の圏 s2-Cat#(r+1) は3-圏になります。

この状況で、どんどん次元が高い圏が出てきてしまいそうですが（一時、僕もそれを恐れてましたが）、圏の次元は上がらないように出来ます。厳密2-圏まで扱えれば無限タワー全体を扱えます。

デカルト構造の無限タワーを構成する素材は次のようなモノです。

k = 0 k = 1 k = 2 K = 3 …
1-圏 0C 1C 2C 3C …
厳密2-圏 1B 2B 3B …

kは無限タワーの階数*3を表す番号です。番号の添字は他の目的の添字とバッティングしないように左肩に付けます。kCは1-圏で、kBは厳密2-圏です。0B は考えないことに注意してください。

これらの1-圏／厳密2-圏達には次の条件があります。

  • kC ∈ 0 k+1B
  • t1(kB) = kC

'∈0' は上で説明済み、t1 は切り落とし〈truncation〉で、2-圏が持つ2-射をすべて捨てて、1-圏とみなす操作です。kC ∈ 0 k+1B から、kC ∈ 0 k+1C も言えます。なぜなら、K+1C の対象と射は、k+1B とまったく同じだからです*4。

この関係の最初のほうを書き出すと：

  1. 0C ∈0 1B, t1(1B) = 1C
  2. 1C ∈0 2B, t1(2B) = 2C
  3. 2C ∈0 3B, t1(3B) = 3C

我々の目的は、タワーの最下段にある圏（通常の1-圏）0C にデカルト構造〈デカルト・モノイド構造〉を定義することです。定義のためには、環境である 1B が必要です。このとき、1B の1-圏パートである 1C にデカルト構造が要求されます。それを定義するには、環境 2B が必要となり、そこでまた… … この過程が無限に繰り返されます。

無限の繰り返しではあっても、「同じことの繰り返し」になってしまえば問題はありません。「同じことの繰り返し」に落ち着いてくれるとき、無限タワーは安定する／安定している〈stabilized | stable〉ということにします。無限タワーが安定しているなら、そこでの無限先送り論法は合理的だと言えるでしょう。

繰り返しの記述法： 左肩に番号

階層構造があるとき、記述に使う文字を階層ごとに変えることがあります。書体を変えたり文字飾りを付けたりします*5。しかし、この方法は無限階層では使えないので、階層の識別は左肩の番号を使います。

ただし、タワーの最初のほうの5つの1-圏／厳密2-圏には特有な記号（固有名詞）を割り当てましょう。

  1. Set := 0C = 0-Cat#0 （1-圏）
  2. CAT := 1B = 1-Cat#1 （厳密2-圏）
  3. CAT1 := 1C = t1(CAT) = t1(1-Cat#1) （1-圏）
  4. CAT := 2B = 1-Cat#2 （厳密2-圏）
  5. CAT1 := 2C = t1(CAT) = t1(1-Cat#2) （1-圏）

階数0の宇宙*6は通常の宇宙〈デフォルトの宇宙 | 作業宇宙〉であり、タワーの最下段の圏は集合圏だとします。集合圏Setが棲む環境CATは、必ずしも小さくない圏の厳密2-圏です。CATを1次元に切り落としたCAT1 は、2-射を持たない1-圏なので、CATから自然変換を捨ててしまった“圏と関手の1-圏”です。そのCAT1は、厳密2-圏CATの対象です。

デカルト構造の構成素も左肩の番号で識別しますが、先に、一般的な意味を番号無しで説明します。

唯ひとつの対象と恒等だけを持つ自明な圏〈trivial category〉を I で示します。I の唯一の対象は常に（階層に無関係に）0だとします。|I| = {0} ですね。C の終対象（兼単位対象）をポイントする関手を i:|→C として、i(0) は 1 （数字のイチ）で書きます。1 はCの対象です。階数の番号を付けた幾つか例を挙げます。

  1. 0i:0I→0C in 1B,
    0i(0) = 01 ∈0 0C
  2. 1i:1I→1C in 2B,
    1i(0) = 11 ∈0 1C
  3. 2i:2I→2C in 3B,
    2i(0) = 21 ∈0 2C

特有な記号（固有名詞）を使えば：

  1. 0i:0I→Set in CAT,
    0i(0) = 01 ∈0 Set
  2. 1i:1I→CAT1 in CAT,
    1i(0) = 11 ∈0 CAT1
  3. 2i:2I→CAT1 in 3B,
    2i(0) = 21 ∈0 CAT1

I, i, 1 は見た目が似てますから見間違えないように注意してください。kI において、kが違っても同じ圏をさすかも知れません。左肩の数値は、実体を識別するのではなくてタワー（という組織）のなかでの位置付け・役割を識別するものです。次の関係があります*7。

  • kI = k+11

デカルト圏〈デカルト・モノイド圏〉のモノイド積を × で表します。× は中置演算子記号なので、まったく同義の関手記号として P も使います。タワーにおける階数を k で表すと：

  • kP:(kC) k+1× (kC) → (kC) in k+1B

左肩の番号がけっこう鬱陶しい。中置演算子記号の × に関しては番号を省略していいことにしましょう*8。

  • kP:kC × kC → kC in k+1B

× の左右の番号は同じなので、× は1を足した番号を持つと解釈します。幾つかの例を出すと：

  1. 0P:0C × 0C → 0C in 1B （× = 1× = 1P）
  2. 1P:1C × 1C → 1C in 2B （× = 2× = 2P）
  3. 2P:2C × 2C → 2C in 3B （× = 3× = 3P）

特有な記号（固有名詞）を使えば：

  1. 0P:Set × Set → Set in CAT （× = 1× = 1P）
  2. 1P:CAT1 × CAT1 → CAT1 in CAT （× = 2× = 2P）
  3. 2P:CAT1 × CAT1 → CAT1 in 3B （× = 3× = 3P）

大ざっぱに言えば、kP と ki により、各 kC がデカルト圏になります。

  1. (0C, 0P, 0i) は、厳密2-圏 1B 内のデカルト圏
    • モノイド積 0P:0C × 0C → 0C in 1B
    • モノイド単位 0i:0I → 0C in 1B
  2. (1C, 1P, 1i) は、厳密2-圏 2B 内のデカルト圏
    • モノイド積 1P:1C × 1C → 1C in 2B
    • モノイド単位 1i:1I → 1C in 2B
  3. (2C, 2P, 2i) は、厳密2-圏 3B 内のデカルト圏
    • モノイド積 2P:2C × 2C → 2C in 3B
    • モノイド単位 2i:2I → 2C in 3B

特有な記号（固有名詞）を使えば：

  1. (Set, 0P, 0i) は、厳密2-圏 CAT 内のデカルト圏
    • モノイド積 0P:Set × Set → Set in CAT
    • モノイド単位 0i:0I → Set in CAT
  2. (CAT1, 1P, 1i) は、厳密2-圏 CAT 内のデカルト圏
    • モノイド積 1P:CAT1 × CAT1 → CAT1 in CAT
    • モノイド単位 1i:1I → CAT1 in CAT
  3. (CAT1, 2P, 2i) は、厳密2-圏 3B 内のデカルト圏
    • モノイド積 2P:CAT1 × CAT1 → CAT1 in 3B
    • モノイド単位 2i:2I → CAT1 in 3B

構造の構成素としての自然変換

前節で、デカルト構造が載った集合圏を (Set, 0P, 0i) と書きましたが、0P を 0× と書いて、0i の代わりに 01 を使って (Set, 0×, 01) と書いてもいいでしょう。通常は、左肩の番号を省略して (Set, ×, 1) と書いているのです。1 を数のイチと混同されるのを嫌って (Set, ×, 1) （太字のイチ）としたりもします。

さて、デカルト圏というのは直積 × と単位対象 1 だけで構成されるのか、というと、それは違います。たくさんの自然変換が必要です。それらの自然変換もちゃんと書けば、

  • デカルト構造が載った集合圏 = (Set, ×, 1, α, λ, ρ, σ, !, δ, π1, π2)

となります。タワーのなかでの位置付け（階数）を考えれば、すべての構成素〈constituents〉に左肩番号が付きますから、

  • デカルト構造が載った集合圏 = (Set, 0×, 01, 0α, 0λ, 0ρ, 0σ, 0!, 0δ, 0π1, 0π2)

となります。デカルト構造の構成素である自然変換達（kα など）にも、無限タワーのなかでキチンとした意味を与える必要があります。

自然変換は2-射なので、厳密2-圏 kB のなかに居ます。例えば、結合律子 α に関して言えば：

  1. 0α は、厳密2-圏 1B の2-射である。
  2. 1α は、厳密2-圏 2B の2-射である。
  3. 2α は、厳密2-圏 3B の2-射である。

特有な記号（固有名詞）を使えば：

  1. 0α は、厳密2-圏 CAT の2-射である。
  2. 1α は、厳密2-圏 CAT の2-射である。
  3. 2α は、厳密2-圏 3B の2-射である。

厳密2-圏 kB は、それらが基礎付けされる宇宙が異なる（kB は Uk に居る）だけで、公理的圏論的構造は同じです。したがって、パラメータとなる番号〈階数〉が異なるだけで同じ記述が得られると期待できます。

自然変換の成分と公平タプル

自然変換 0α に関して見ると、0α は次のプロファイルを持ちます。以下、0C の恒等関手は (0C)^ という書き方をします。

  • 0α :: (0P × (0C)^) ; 0P ⇒ (1α)0C,0C,0C ; ((0C)^ × 0P) ; 0P in 1B

ここで、記号 '×', ';' は 1C（1B の対象と射の部分）で定義されている直積、結合です。(1α)0C,0C,0C は、2B の2-射〈自然変換〉1α の成分です。1α の成分は 1C の射となります（1C の射とは 1B の射でもあります）。

次でも同じ意味でした。

  • 0α :: (0P × Set^) ; 0P ⇒ (1α)Set,Set,Set ; (Set^ × 0P) ; 0P in CAT

Set（a.k.a. 0C）のデカルト構造を記述するには、CAT（a.k.a. 1B）の2-射である自然変換 0α が必要です。そして、0α のプロファイル記述のなかに、CAT（a.k.a. 2B）の2-射 1α の成分が登場します。

一般に、タワーのk階に居るデカルト圏を定義するのは、それより2階上に居る2-圏 k+2B の2-射（自然変換）を必要とします。しかし、自然変換の全貌が必要なわけではなくて、特定の成分です。k+2B の自然変換の成分は、k+1C（あるいは k+1B）の射になります。

このような状況を把握・理解するには、「自然変換の成分をとる」行為が必須です。「成分をとる」とは、記法の上ではインデックス（通常は下付き添字）を付けることです。例えば、（適当な階数の）結合律子 α に対して、αA,B,C とすることです。

ここで、問題が生じます。インデックス A,B,C をタプル (A, B, C) と解釈すると、((A, B), C) か (A, (B, C)) か気になります。((A, B), C) と (A, (B, C)) を対応させるためには結合律子が必要になり、またしても循環論法的状況が生じます。

この問題を回避するには、インデックスに使うタプルは公平タプル〈unbiased tuple〉だとすればいいでしょう。集合Xに対して次のように定義します。Map(-, -) は写像〈関数〉の集合です。

  1. X[0] := Map({}, X)
  2. X[1] := Map({1}, X)
  3. X[2] := Map({1, 2}, X)
  4. X[3] := Map({1, 2, 3}, X)
  5. 以下同様

例えば、ξ∈X[3] が、ξ(1) = a, ξ(2) = b, ξ(3) = c のとき、ξ = [a, b, c] と書きます。このような定義や書き方は、どの宇宙 Ur でも有効です。

自然変換の成分インデックスは、圏の対象集合のタプルですが、上記の公平タプルを採用すれば、「((A, B), C) と (A, (B, C)) の違い」を気にする必要がなくなります。次のように言えます。

  • αA,B,C は、α[A,B,C] のことであり、[A, B, C] は公平タプルである。

異なる（かも知れない）n個の集合の列 X1, ..., Xn に対しても、これらの集合の（この順での）公平タプルを定義できます。すべての宇宙で通用する公平タプルの理論を事前に準備しておけば、インデックスの悩みは解消します。

安定する無限タワーの構造

横方向に圏の次元をとり、縦方向に宇宙の階数をとった平面内に圏論的実体達〈category-theoretic entities〉を配置することにします。無限タワーを意識し始めた頃、僕が恐怖を感じたのは、0-Cat#0 ∈0 1-Cat#1 ∈0 2-Cat#2 ∈0 ... という無限系列（図では対角線）です*9。

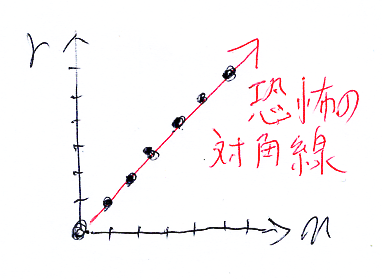
図の対角線は、いわば恐怖の対角線〈fearful diagonal〉。もし、対角線方向に無限タワーが伸びるなら、次元も階数もどんどん上がり、とても手におえそうにありません。

しかし、現実に我々が無限先送り論法を使っているということは、何らかの理由で恐怖の対角線から逃れているのでしょう。その何らかの理由とは、無限タワーは次元方向には伸び続けない、ということです。

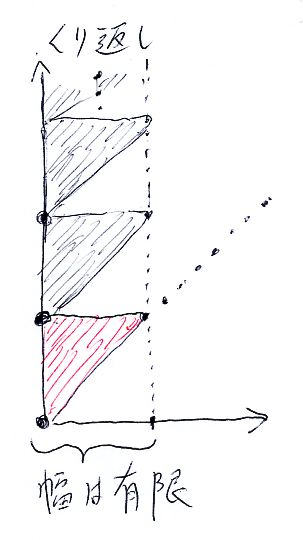
ある程度は次元方向（図の横方向）へもタワーは拡がりますが、ある所からは階数が増えるだけです。階数が増えるだけになると、それは「同じことの繰り返し」となります。デカルトタワーに限らず、安定する無限タワーは同様な構造を持つのでしょう。一言にまとめれば：

  • 安定するタワーは、幅が有限である。

デカルト構造の無限タワー〈デカルト・タワー〉、モノイド構造の無限タワー〈モノイド・タワー〉をシッカリ理解すれば、安定するタワーの一般論も見えてきそうです。安定するタワーが、マイクロコスモス原理の仕掛けなのだと思います。

最後に僕の漠然とした印象を述べます。無限先送りを繰り返しに帰着させるためには、タワーの幅を有限に抑える必要があります。しかし、幅有限に抑えることは人為的な細工である気がします。“野生の圏論的実体達“は、恐怖の対角線に沿って伸びようとする、と思えるのです。例えば、2-圏にデカルト構造を載せたデカルト2-圏を考えると、横（圏の次元）方向にタワーが拡がります。

本来、横（次元の方向）にも伸びようとする力が働くなかで、その力を抑制あるいは封印してタワーを安定化させているのです。次元方向への伸びも取り扱えれば望ましいのは言うまでもありません（が、難しい）。

*1:https://ncatlab.org/nlab/show/microcosm+principle をそのまま引用すると： "Microcosm principle: Certain algebraic structures can be defined in any category equipped with a categorified version of the same structure." 訳文：「マイクロコスモ原理： 特定の代数構造は、その代数構造を圏化した構造を備える圏のなかで定義可能である。」

*2:元画像： https://www.pinterest.dk/pin/293156256988127896/

*3:宇宙の階数とタワーの階数の定義は一応別ですが、今回の話では、宇宙の階数とタワーの階数は一致します。タワーのr階に居る圏は、階数rの小圏／小厳密2-圏です。

*4:1-圏に自明な2-射を考えて2-圏とみなすと、C-系列はB-系列に埋め込めます。

*5:書体を変えたり文字飾りを付けたりは僕もよく使います。けど、毎回いきあたりばったりで、系統的な規則は決めてないです。

*6:実際には、U0 の下にも宇宙があるかも知れませんが、基準とする宇宙が U0 です。

*7:この関係があるので、文字 I を使わなくてもいいですが、見やすさのために I も入れておきます。

*8:「デカルト構造の無限タワー： 怖がらずに登れ」では、階数がひとつ上のモノを表す記号にはダッシュ〈プライム〉（シングルクォートで代用）を打つダッシュ記法を使いました。

*9:圏の次元が2以上だと、さらに「弱さ」のバラエティが追加されます。「高次圏： 複雑さの2つの方向と半厳密性」参照。