クロムウェルのルールと確率空間の同値 - 檜山正幸のキマイラ飼育記 (はてなBlog)

$\newcommand{\u}[1]{\underline{#1}} \newcommand{\Pow}{\mathrm{Pow} } \newcommand{\Imp}{\Rightarrow } \newcommand{\Iff}{\Leftrightarrow } \newcommand{\Null}{\mathrm{Null} } \newcommand{\Id}{\mathrm{Id}} \newcommand{\twoTo}{\Rightarrow } \newcommand{\twoV}{\mathop{\&} } \newcommand{\eqv}{\overset{\sim}{\equiv}} \newcommand{\id}{\mathrm{id} } \newcommand{\In}{\text{ in } } \require{color} \newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }% \newcommand{\For}{\Keyword{For } }% \newcommand{\Define}{\Keyword{Define } }% \newcommand{\Where}{\Keyword{Where } }% \newcommand{\When}{\Keyword{When } }% \newcommand{\Holds}{\Keyword{Holds } }% \newcommand{\Then}{\Keyword{Then } }%$ ひょんなことから、クロムウェルのルール〈Cromwell's rule〉というものを知りました。クロムウェルのルールを確率の議論に適用すると、「確率 0 の事象なんてない」ってことになるようです。僕の感想は、「そんなバカな。確率 0 の事象なんていくらでもあるでしょ」。例えば、明日の朝、太陽が西から昇る確率は 0 でしょ。

しかし、タチのよい確率空間に限定した話にすると、次の形でクロムウェルのルールをある程度は正当化できます。

確率 0 の“非空な事象”がない確率空間だけを考えてもよい。

この正当化は、もともとのクロムウェルのルールの意図を捻じ曲げているかも知れませんけどね。

内容：

クロムウェルのルール
確率空間と確率保存写像
確率保存写像のあいだの同値関係
ホムセット上の同値関係と圏の構造
確率空間の2-圏
確率空間の同値
強いクロムウェルのルールを守る確率空間
強いクロムウェルのルールを守る代替物
箴言としてのクロムウェルのルール

クロムウェルのルール

クロムウェルのルールに関する説明は英語版Wikipediaしか見てません。それによると、クロムウェルの次の言葉が語源のようです。

I beseech you, in the bowels of Christ, think it possible that you may be mistaken.

よく分かりません。"in the bowels of Christ" って何のこと？分からないのでこの句を無視すると、「あなたが間違っている可能性だってゼロとは言えないのじゃないの」みたいなことでしょう。

別な引用として、次の言葉もあります。

leave a little probability for the moon being made of green cheese;

月がグリーンチーズからできているという僅かな可能性〈確率〉も残す、とのこと。どうやら、この世に絶対に起きない（あるいは絶対に起きる）事象はないと主張したいようです。

現実世界では絶対なんてないのだから、太陽が西から昇る僅かな可能性〈確率〉も残すべきってことです。なんか腑に落ちないな、僕は。

確率に関する強いクロムウェルのルール〈a strengthened version of Cromwell's rule〉だと、事象 A の確率 Pr(A) に次の制限を設けるとのこと。

0 < Pr(A) < 1

Pr(A) = 0 と Pr(A) = 1 は認めないわけです。なんか腑に落ちないな、僕は。

上記の強いクロムウェルのルールって、確率の議論に適用していいもんなんでしょうか？次節以降で考えてみます。

確率空間と確率保存写像

$X = (\u{X}, \Sigma_X, \mu_X)$ を確率空間〈probability space〉とします。ここで：

台集合： $\u{X}$ は集合
シグマ代数： $\Sigma_X$ は、台集合 $\u{X}$ のベキ集合 $\Pow(\u{X})$ の部分集合であるシグマ代数
確率測度： $\mu_X$ は、シグマ代数 $\Sigma_X$ 上の測度であって $\mu(\u{X}) = 1$ を満たすもの

記号の乱用を用いずに、確率空間とその台集合は区別しています。が、この方針を徹底する気はありません。例えば、シグマ代数がベキ集合の部分集合であることを $\Sigma_X \subseteq \Pow(\u{X})$ と書くのは不正確で、シグマ代数の台集合を使って $\u{\Sigma_X} \subseteq \Pow(\u{X})$ と書くべきでしょう*1が、そこまではやりません（めんどうだから）。

台集合 $\u{X}$ の部分集合 $A\subseteq \u{X}$ が $A\in \Sigma_X$ （ここは記号の乱用）のとき、 $A$ を可測集合〈measurable set〉または事象〈event〉と呼びます。（確率空間の可測集合を特に事象と言うようです）。 $\u{X}$ と $\emptyset$ は事象で、次の確率を持ちます。

$\quad \mu_X(\u{X}) = 1\\ \quad \mu_X(\emptyset) = 0$

$X = (\u{X}, \Sigma_X, \mu_X),\, Y = (\u{Y}, \Sigma_Y, \mu_Y)$ を2つの確率空間として、台集合のあいだの写像 $f:\u{X} \to \u{Y}$ が次を満たすとき可測写像〈measurable map〉といいます。

$\quad \forall B \in \Sigma_Y.\, f^{-1}(B) \in \Sigma_X$

ここで、 $f^{-1}$ は逆写像ではなくて逆像を対応させる写像です。

可測であるだけでなく、さらに次の条件も満たすときは測度を保存する〈preserve measure | measure-preserving〉といいます。

$\quad \forall B \in \Sigma_Y.\, \mu_X(f^{-1}(B)) = \mu_Y(B)$

確率空間に備わっている測度 $\mu_X,\, \mu_Y$ は確率測度なので、測度を保存する可測写像は確率保存写像〈probability-preserving map〉とも呼びます。

確率空間を対象として、確率保存写像を射とする圏を構成できるので、この圏を ${\bf PS}$ と書きます。確率保存写像は、圏論的な言葉で確率空間射〈morphism of probability spaces〉ともいえます。

確率空間の圏には他の定義もあって、射として可測写像ではなくてマルコフ核を使うバージョンもあります。が、ここでは使いません。

確率保存写像のあいだの同値関係

確率空間 $X$ の事象 $A$ が次を満たすときゼロ事象〈null event〉と呼びます。

$\quad \mu_X(A) = 0$

ゼロ事象の別な定義もあるようですが、ここでは割り切った上記の定義を採用します。確率空間 $X$ のゼロ事象の全体を $\Null_X$ とします。

議論を簡単にするために、以下、次の性質を仮定します。

$\quad \forall A \in \Sigma_X.\forall B \in \Pow(\u{X}).\, \mu_X(A) = 0\land B\subseteq A \Imp B \in\Sigma_X \land \mu_X(B) = 0\\ \quad \Delta_{\u{X}} \in (\Sigma_X \otimes \Sigma_X)$

ゼロ事象の部分集合はゼロ事象で、対角集合 $\Delta_{\u{X}} \subseteq \u{X}\times \u{X}$ は直積集合内の可測集合になるってことです。十分タチのよい確率空間なら、この性質が成立しているとしていいでしょう。

確率空間のあいだの可測写像 $f, g:X \to Y$ がほとんど等しい〈almost equal | almost surely equal〉とは次のことです。

$\quad \exists N\in \Null_X.\, f|_{\u{X}\setminus N} = g|_{\u{X}\setminus N}$

$f, g$ がほとんど等しいことを $f \sim g$ と書くことにします。

$f \sim g$ とは、 $f, g$ がホントに等しいとは限りませんが、等しくない点はゼロ事象なので“無視できる例外点”ということです。別な言い方をすると、確率 1 の部分集合上で等しいことが“ほとんど等しい”ことです。

“ほとんど等しい”に関する議論を簡略化するために、述語（真偽値を値とする写像） $p:\u{X} \to \{\mathrm{True}, \mathrm{False}\}$ に対して、次の記法を導入します。

$\quad [p] := \{x\in \u{X}\mid p(x) = \mathrm{True}\}$

$[p] \subseteq \u{X}$ が可測集合〈事象〉になるとき、述語は可測述語〈measurable predicate〉だと言うことにします。述語が可測な場合は、その確率を次のように書きます。

$\quad \mu_X [p] := \mu_X( [p] )$

単に丸括弧を省いていいというルールを設けただけです。

さて、対角集合が可測であるという仮定のもとでは、可測写像 $f, g:X \to Y$ に対する $[f = g]$ は事象〈可測集合〉になります。なぜなら：

$\quad [f = g]\\ = \{x\in \u{X}\mid f(x) = g(x)\}\\ = \langle f, g\rangle^{-1} (\Delta_{\u{Y}}) \\ \Where\\ \quad \langle f, g\rangle := \lambda\, x\in \u{X}.(\, (f(x), g(y)) \;\in \u{Y}\times \u{Y}\,)$

これと、 $f, g$ が可測なら $\langle f, g\rangle$ が可測なこと、可測写像による可測集合の逆像は可測なこと（定義）を使います。

今述べたセッティングでは、 $f, g$ がほとんど等しいことは次のように言い換えられます。

$\quad \mu_X[f = g] = 1$ （ $f, g$ が等しい確率は 1）

あるいは、同じことですが、

$\quad \mu_X[f \ne g] = 0$ （ $f, g$ が等しくない確率は 0）

この形の定義は、心理的に自然で運用しやすいのではないかと思います。例えば、“ほとんど等しい”の推移律を示してみましょう。

$\mu_X[f \ne g] = 0 \land \mu_X[g \ne h] = 0$ を仮定して計算してみます。

$\quad \mu_X [f \ne g \lor g \ne h]\\ = \mu_X( [f \ne g] \cup [g \ne h] )\\ \le \mu_X[f \ne g] + \mu_X[g \ne h] ) = 0\\ \Then\\ \quad \mu_X [f \ne g \lor g \ne h] = 0\\ \:\\ \quad \mu_X [f = g \land g = h]\\ = \mu_X [\lnot (f \ne g \lor g \ne h)]\\ = 1 - \mu_X [f \ne g \lor g \ne h]\\ = 1 - 0 = 1\\ \Then\\ \quad \mu_X [f = g \land g = h] = 1$

“ほとんど等しい”の反射律と対称律は明らかなので、“ほとんど等しい”関係 $\sim$ は、 $X$ から $Y$ への可測写像の集合上の同値関係になります。確率保存写像は可測写像なので、“ほとんど等しい”関係を確率保存写像の集合上に制限してもかまいません。

ホムセット上の同値関係と圏の構造

圏論の習慣に従うと、確率空間 $X$ から $Y$ のすべての射（確率保存写像）の集合は ${\bf PS}(X, Y)$ と書き、ホムセット〈homset〉といいます。前節の結果より、各 ${\bf PS}(X, Y)$ ごとに“ほとんど等しい”という同値関係が入ったわけです。

異なるホムセット上の“ほとんど等しい”を区別したいときは次のように書きます。

$\sim_{X, Y} \text{ on }{\bf PS}(X, Y)$
$\sim_{Y, Z} \text{ on }{\bf PS}(Y, Z)$

各ホムセットごとに与えられた“ほとんど等しい”という同値関係は、圏の構造と整合性〈互換性 | compatibility〉を持ちます。それは次のことです。

$\For X, Y, Z \in |{\bf PS}|\\ \For f, f'\in {\bf PS}(X, Y)\\ \For g, g'\in {\bf PS}(Y, Z)\\ \Holds f \sim_{X, Y} f' \,\land\, g \sim_{Y, Z} g' \,\Imp f;g \sim_{X, Z} f';g'$

ここで、セミコロンは射の結合の図式順記号です。反図式順記号は白丸 $\circ$ です。

上記の命題は、 $\mu_X[f \ne f'] = 0 \,\land\, \mu_Y[g \ne g'] = 0$ の仮定のもとで、次の集合の確率を計算すればわかります。

$\quad [f;g \ne f';g'] \\ = \{x\in \u{X} \mid g(f(x))\ne g'(f'(x)) \} \subseteq \u{X}$

計算してみましょう。まず次の事実に注意します。（共通部分がない集合の合併にはプラス記号を使っています。）

$\quad \mu_X(B) \\ = \mu_X(\u{X} \cap B) \\ = \mu_X( (A + A^c) \cap B) \\ = \mu_X( (A\cap B) + (A^c \cap B) )\\ = \mu_X( A\cap B ) + \mu_X( A^c \cap B )$

これを使うと次が言えます。

$\quad \mu_X[f;g \ne f';g'] \\ = \mu_X( [f = f']\cap [f;g \ne f';g'] ) + \mu_X( [f \ne f'] \cap [f;g \ne f';g'] )$

足し算している二番目の項を見ると：

$\quad \mu_X( [f \ne f'] \cap [f;g \ne f';g'] ) \le \mu_X( [f \ne f'] )= 0\\ \Then\\ \quad \mu_X( [f \ne f'] \cap [f;g \ne f';g'] ) = 0$

したがって、一番目の項だけ計算すればOKです。一番目の項の引数を変形します（下に補足あり）。

$\quad [f = f']\cap [f;g \ne f';g'] \\ = [f = f' \land f;g \ne f';g'] \\ = \{x\in \u{X} \mid f(x) = f'(x) \land g(f(x)) \ne g'(f'(x)) \}\\ = \{x\in \u{X} \mid f(x) = f'(x) \land g(f(x)) \ne g'(f(x)) \}\\ = [f = f' ] \cap f^{-1}([g \ne g'])$

上記集合の確率測度は、 $f$ が確率保存写像であることを使って*2計算します。

$\quad \mu_X( [f = f' ] \cap f^{-1}([g \ne g']) )\\ \le \mu_X( f^{-1}([g \ne g']) ) \\ = \mu_Y[g \ne g'] = 0\\ \Then\\ \quad \mu_X( [f = f' ] \cap f^{-1}([g \ne g']) ) = 0$

結局：

$\quad \mu_X[f;g \ne f';g'] = 0$

[補足]上で、次の命題を使っています。

$(f(x) = f'(x) \land g(f(x)) \ne g'(f'(x))) \Iff (f(x) = f'(x) \land g(f(x)) \ne g'(f(x)))$
$\{x\in \u{X}\mid g(f(x)) \ne g'(f(x) \} = f^{-1}([ g \ne g'])$

自明に見える人もいれば戸惑う人もいるかもしれません。

一番目の命題は次の4つの命題に分解できます。

$(f(x) = f'(x) \land g(f(x)) \ne g'(f'(x))) \Imp f(x) = f'(x)$
$(f(x) = f'(x) \land g(f(x)) \ne g'(f'(x))) \Imp g(f(x)) \ne g'(f(x))$
$(f(x) = f'(x) \land g(f(x)) \ne g'(f(x))) \Imp f(x) = f'(x)$
$(f(x) = f'(x) \land g(f(x)) \ne g'(f(x))) \Imp g(f(x)) \ne g'(f'(x))$

それぞれは明らかでしょう。よって、先の一番目の命題は成立します。

次に、集合 $f^{-1}([ g \ne g'])$ について考えます。

$\quad x \in f^{-1}([ g \ne g'])\\ \Iff f(x) \in [ g \ne g']\\ \Iff f(x) \in \{ y \in \u{Y} \mid g(y) \ne g'(y) \}\\ \Iff g(f(x)) \ne g'(f(x))$

これで、 $\{x\in \u{X}\mid g(f(x)) \ne g'(f(x) \} = f^{-1}([ g \ne g'])$ が言えました。
[/補足]

確率空間の2-圏

ここまでで、各ホムセット上に都合がいい同値関係が載った圏 ${\bf PS}$ を構成できました。 $f \sim_{X,Y} g$ という写像間の同値を2-射とみなすことにより、 ${\bf PS}$ を2-圏とみなすことにします。2-圏とは、対象（点で図示）と射（矢印で図示）以外に、2-射（二重矢印で図示）も持つ圏論的構造物です。

$f \sim_{X,Y} g$ を次のように書きます。

$\quad \alpha:: f \twoTo g : X \to Y \In {\bf PS}$

通常は、写像間の同値にいちいち名前を付けたりしませんが、ここでは $\alpha$ と名付けています。 $\sim$ が同値関係であることを、この書き方に書き換えてみます。

反射律：

$\For f: X \to Y \In {\bf PS}\\ \Holds f \sim_{X, Y} f$

次のように書き換えます。射〈1-射〉に対する恒等2-射があるとします。

$\For f: X \to Y \In {\bf PS}\\ \Holds \Id_f :: f \twoTo f : X \to Y \In {\bf PS}$

対称律：

$\For f, g : X \to Y \In {\bf PS}\\ \When f \sim_{X, Y} g\\ \Holds g \sim_{X, Y} f$

次のように書き換えます。2-射には必ず逆があると想定しています。

$\For f, g : X \to Y \In {\bf PS}\\ \When \alpha :: f \twoTo g : X \to Y \In {\bf PS}\\ \Holds \alpha^{-1} :: g \twoTo f : X \to Y \In {\bf PS}$

推移律：

$\For f, g, h: X \to Y \In {\bf PS}\\ \When f \sim_{X, Y} g\\ \When g \sim_{X, Y} h\\ \Holds g \sim_{X, Y} h$

次のように書き換えます。2-射の縦結合（演算記号は $\&$ 、下に図あり）があると想定しています。

$\For f, g, h: X \to Y \In {\bf PS}\\ \When \alpha :: f \twoTo g : X \to Y \In {\bf PS}\\ \When \beta :: g \twoTo h : X \to Y \In {\bf PS}\\ \Holds \alpha \twoV \beta :: f \twoTo h : X\to Y \In {\bf PS}$

前節の“ほとんど等しい”と圏の結合との整合性も書き換えましょう。

$\For f, f': X \to Y \In {\bf PS}\\ \For g, g': Y \to Z \In {\bf PS}\\ \When f \sim_{X, Y} f'\\ \When g \sim_{Y, Z} g'\\ \Holds f;g \sim_{X, Z} f';g'$

これは次のように書けます。2-射の横結合（演算記号は $;$ 、下に図あり）になります。

$\For f, f': X \to Y \In {\bf PS}\\ \For g, g': Y \to Z \In {\bf PS}\\ \When \alpha :: f \twoTo f' : X \to Y \In {\bf PS}\\ \When \beta :: g \twoTo g' : Y \to Z \In {\bf PS}\\ \Holds \alpha;\beta :: f;g \twoTo f';g' : X\to Z \In {\bf PS}$

2-射の縦結合と横結合を理解するには次の図が役立つかも知れません。上が横結合の状況、下が縦結合の状況です。

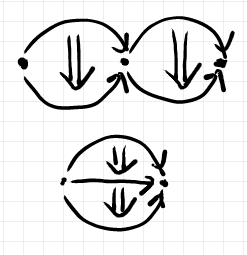
以上で、圏 ${\bf PS}$ の1-射のあいだの2-射が定義できて、恒等2-射、2-射の逆、2-射の縦結合、2-射の横結合が定義できました。2-圏であるためには、幾つかの法則を要求されますが、それは割愛します。

${\bf PS}$ の各ホムセットに2-射も付け加えることにより圏が形成されます。これをホム圏〈homcategory〉といいます。ホム圏も ${\bf PS}(X, X)$ と書きますが、今後は圏として扱います。次のことに注意してください。

$\quad (\, f:X\to Y \In {\bf PS} \,) \Iff (\, f \in |{\bf PS}(X, Y)|\,)\\ \quad (\, \alpha :: f \twoTo g :X \to Y \In {\bf PS}\,) \Iff (\, \alpha :f \to g \In {\bf PS}(X, Y)\,)\\ \quad (\, \alpha :f \to g \In {\bf PS}(X, Y) \,)\Iff (\, \alpha \in {\bf PS}(X, Y)(f, g)\,)$

同値関係“ほとんど等しい”から作ったホム圏は非常に特殊な圏で次の特徴を持ちます。

ホム圏のすべての射は可逆である。同値関係の対称律に相当します。
ホム圏のホムセットは単元集合または空集合。このような圏をやせた圏〈thin category〉といいます。

確率空間の同値

${\bf PS}$ の2-圏構造を利用して、2つの確率空間が同値〈equivalent〉であること（記号は $\eqv$ ）を定義します。定義内に出てくる $\cong$ はホム圏内の同型です。似た記号 $\eqv,\, \cong$ を区別してください。

$\For X, Y \in |{\bf PS}|\\ \Define X \eqv Y \In {\bf PS} \\ :\Iff \exists\, f:X \to Y,\; g : Y\to X \In {\bf PS}.\, \\ \qquad f; g \cong \id_X \In {\bf PS}(X, X)\\ \qquad \land \\ \qquad g ; f \cong \id_Y \In {\bf PS}(Y, Y)$

2-圏 ${\bf PS}$ におけるホム圏内の同型 $\cong$ とは、確率保存写像のあいだの“ほとんど等しい”関係のことでした。よって、次のように書いても同じです。

$\For X, Y \in |{\bf PS}|\\ \Define X \eqv Y \In {\bf PS} \\ :\Iff \exists\, f:X \to Y,\; g : Y\to X \In {\bf PS}.\, \\ \qquad f; g \sim_{X, X} \id_X\\ \qquad \land \\ \qquad g ; f \sim_{Y, Y} \id_Y$

2つの確率空間の同値性 $X \eqv Y$ は、同型性 $X \cong Y$ よりゆるい分類を与えます。同型ではくても同値になる確率空間のペアがあります。まったくつまらない例ですが、同型ではないが同値である確率空間 $X, Y$ の例を挙げます。

確率空間 $X$ を次のように定義します。

$\u{X} = \{0\}$
$\Sigma_X = \{\emptyset, \{0\} \}$
$\mu_X(\emptyset) = 0,\, \mu_X(\{0\} ) = 1$

確率空間 $Y$ を次のように定義します。

$\u{Y} = {\bf R}$
$\Sigma_X = \Pow({\bf R})$
$\mu_X := \lambda\, A\in \Pow({\bf R}).(\,\text{if }0\in A \text{ then } 1\text{ else } 0 \,)$

写像 $f:\u{X} \to \u{Y}$ を次のように定義します。

$f(0) = 0 \;\in {\bf R} = \u{Y}$

写像 $g:\u{Y} \to \u{X}$ を次のように定義します。

$g(x) = 0 \;\in \{0\} = \u{X} \:\text{ for }x\in {\bf R} = \u{Y}$

$f, g$ は確率保存写像になります。そればかりではなく次が成立します。

$f;g \sim_{X, X} \id_X$
$g;f \sim_{Y, Y} \id_Y$

$f;g =\id_X$ なので一番目は自明に成立しています。二番目に関しては、確率空間 $Y$ のゼロ事象 $N := {\bf R}\setminus \{0\}$ を考えます。このゼロ事象に関して、次が成立します。

$\quad (g;f)|_{\u{Y} \setminus N} = (\id_Y)|_{\u{Y} \setminus N}$

これは、次のように書き換えてみれば明らかですね。

$\quad (g;f)|_{ \{0\} } = (\id_Y)|_{ \{0\} }$

ゼロ事象 $N$ を除いた部分（それが 0 だけ）で等しいので“ほとんど等しい”のです。

以上から、 $X \eqv Y$ が分かりました。しかし、 $X \cong Y$ にはなりません。そもそも、集合としての1：1写像 $f : \u{X} \to \u{Y}$ が存在しないので。

[補足]2-圏 ${\bf PS}$ のホム圏内の同型は“ほとんど等しい”なので、同型の一般的な定義に戻る必要はありませんでした。ホム圏内の同型の定義を律儀に書き下すと次のようになります。

$\quad f; g \cong \id_X \In {\bf PS}(X, X)\\ :\Iff \exists\, \alpha: f ; g \to \id_X,\; \beta : \id_X\to f; g \In {\bf PS}(X, X).\, \\ \qquad \alpha ; \beta = \id_{f ; g} \\ \qquad \land\\ \qquad \beta ; \alpha = \id_{\id_X}\\ :\Iff \exists\, \alpha:: f ; g \twoTo \id_X: X \to X,\; \beta :: \id_X\twoTo f; g :X \to X \In {\bf PS}.\, \\ \qquad \alpha \twoV \beta = \Id_{f ; g} \\ \qquad \land\\ \qquad \beta \twoV \alpha = \Id_{\id_X}$

$\quad g; f \cong \id_Y \In {\bf PS}(Y, Y)\\ :\Iff \exists\, \varphi: g ; f \to \id_Y,\; \psi : \id_Y\to g; f \In {\bf PS}(Y, Y).\, \\ \qquad \varphi ; \psi = \id_{g ; f} \\ \qquad \land\\ \qquad \psi ; \varphi = \id_{\id_Y}\\ :\Iff \exists\, \varphi :: g ; f \twoTo \id_Y: Y \to Y,\; \psi :: \id_Y\twoTo g; f :Y \to Y \In {\bf PS}.\, \\ \qquad \varphi \twoV \psi = \Id_{g ; f} \\ \qquad \land\\ \qquad \psi \twoV \varphi = \Id_{\id_Y}$
[/補足]

強いクロムウェルのルールを守る確率空間

最初の節で引用した強いクロムウェルのルール〈a strengthened version of Cromwell's rule〉をもう一度述べると、事象 A の確率 Pr(A) は 0 < Pr(A) < 1 を満たすことでした。この制約を、確率空間 $X$ に対して定義すれば次のようになるでしょう。

$\quad \forall A\in \Sigma_X.(\, A \ne \emptyset \land A \ne \u{X} \Imp 0 \lt \mu_X(A)\lt 1 \,)$

この制約を満たす確率空間を強いクロムウェルのルールを守る〈respects strong Cromwell's rule〉ということにします。

強いクロムウェルのルールを守る確率空間では、空事象以外のゼロ事象はありません。逆に、空事象以外のゼロ事象がなければ、強いクロムウェルのルールを守ります。

空事象以外のゼロ事象がないという条件は、実際にはなかなか守れません。例えば、おそらくは最もおなじみの確率測度である実数直線上のガウス確率測度〈正規分布〉を考えると、一点だけの事象〈単元事象 | 根本事象〉は空でないゼロ事象になります。一点だけの集合を事象〈可測集合〉から除くことも、積分やシグマ代数を構成する都合で無理そうです。

強いクロムウェルのルールを守れそうな確率空間とはどんなものでしょうか？台集合が有限の場合なら守れそうです。確率空間 $X$ の台集合 $\u{X}$ が有限集合で、シグマ代数がベキ集合で与えられる場合なら、空でないゼロ事象を持たないことは次のように書けます。

$\quad \forall x\in \u{X}.\, \mu_X(\{x\}) \ne 0$

これが強いクロムウェルのルールになります。一方、強いクロムウェルのルールを守れてない確率空間は次の性質を持ちます。

$\quad \exists x\in \u{X}.\, \mu_X(\{x\}) = 0$

強いクロムウェルのルールについて考えるにあたって、台集合が有限集合である確率空間に限定した確率空間の2-圏 ${\bf FinPS}$ を舞台にすることにします。

強いクロムウェルのルールを守る代替物

冒頭で述べたこと：

タチのよい確率空間に限定した話にすると、次の形でクロムウェルのルールをある程度は正当化できます。

確率 0 の“非空な事象”がない確率空間だけを考えてもよい。

これの話をします。

具体的に言えば、有限な確率空間 $X \in |{\bf FinSP}|$ に対して、次のような $Y \in |{\bf FinSP}|$ が存在します。

$Y$ は強いクロムウェルのルールを守っている。
$X \eqv Y$

同値な確率空間は同類とするなら、同類のなかで強いクロムウェルのルールを守っている確率空間を見つける、あるいは作ることができるわけです。

では、与えられた $X \in |{\bf FinSP}|$ に対して次のモノを構成しましょう。

対象（確率空間） $Y \in |{\bf FinPS}|$
射（確率保存写像） $g :Y \to X \In {\bf FinPS}$
射（確率保存写像） $f :X \to Y \In {\bf FinPS}$
2-射（“ほとんど等しい”関係） $g;f \twoTo \id_Y : Y \to Y \In {\bf FinPS}$
2-射（“ほとんど等しい”関係） $f;g \twoTo \id_X : X \to X \In {\bf FinPS}$

まず確率空間 $Y$ の構成。

$\u{Y} := \{x\in \u{X} \mid \mu_X(\{x\}) \ne 0 \}$
$\Sigma_{Y} := \Pow(\u{Y})$
$\mu_{Y} := \lambda\, B\in \Pow(\u{Y}).\, \mu_X(B)$

一言でいえば、 $X$ から確率ゼロの点を取り除いて作った確率空間が $Y$ です。定義から次が成立するので、 $Y$ は強いクロムウェルのルールを守っています。

$\quad \forall y\in \u{Y}.\, \mu_Y(\{y \}) \ne 0$

写像 $g:\u{Y} \to \u{X}$ は包含写像として定義します。 $g$ が可測なのは明らかなので、確率を保存することを示します。次がターゲット命題です。

$\quad \forall A\in \Pow(\u{X}).\, \mu_Y(g^{-1}(A) ) = \mu_X(A)$

$g^{-1}(A) = A \cap \u{Y}$ であることから、次を示せばいいことになります。

$\quad \forall A\in \Pow(\u{X}).\, \mu_X(A \cap \u{Y}) = \mu_X(A)$

次の計算で示せます。

$\quad \mu_X(A)\\ = \mu_X(\u{X} \cap A)\\ = \mu_X( (\u{Y} + {\u{Y}}^c) \cap A)\\ = \mu_X( (\u{Y}\cap A) + ({\u{Y}}^c \cap A) )\\ = \mu_X( \u{Y}\cap A) + \mu_X({\u{Y}}^c \cap A )\\ = \mu_X( \u{Y}\cap A) + 0\\ = \mu_X( A \cap \u{Y})$

今度は写像 $f:\u{X} \to \u{Y}$ の定義です。 $\u{Y}$ は空ではないので、要素 $b\in \u{Y}$ を選んで固定します。 $f$ は次のようです。

$\quad f := \lambda\, x\in \u{X}.(\,\text{if } x\in \u{Y} \text{ then }x \text{ else }b \,)$

この $g$ が確率を保存することを示します。次がターゲット命題です。

$\quad \forall B\in \Pow(\u{Y}).\, \mu_X(f^{-1}(B) ) = \mu_Y(B)$

2つのケースに場合分けします。

$b \not\in B$
$b \in B$

ケース1のときは $f^{-1}(B) = B$ なので、示すべきことは自明な等式です。ケース2のときは、 $f^{-1}(B) = B + {\u{Y}}^c$ なので、次のように計算できます。

$\quad \mu_X(f^{-1}(B) )\\ = \mu_X(B + {\u{Y}}^c )\\ = \mu_X(B) + \mu_X( {\u{Y}}^c )\\ = \mu_X(B) + 0\\ = \mu_X(B)\\ = \mu_Y(B)$

“ほとんど等しい”関係 $g;f \sim_{Y, Y} \id_Y$ は、 $g;f = \id_Y$ から明らかです。残る“ほとんど等しい”関係は $f;g \sim_{X, X} \id_X$ です。

$N := {\u{Y}}^c = \u{X} \setminus \u{Y}$ と置くと、 $N$ は確率空間 $X$ のゼロ事象になります。次の2つの等式は同じことで、成立する等式です。

$\quad (f;g)|_{\u{Y}} = \id_X|_{\u{Y}}\\ \quad (f;g)|_{\u{X}\setminus N} = \id_X|_{\u{X}\setminus N}$

二番目の等式は $f;g \sim_{X, X} \id_X$ を意味します。

以上で、確率空間 $X$ から構成した確率空間 $Y$ は次の性質を持つことが分かりました。

$Y$ は強いクロムウェルのルールを守っている。
$X \eqv Y$

箴言としてのクロムウェルのルール

クロムウェルのルールは、ベイズ確率の事前確率を選ぶ際の指針のようです。前節の結果は、最初に選んだ事前確率（が載った確率空間）がクロムウェルのルールを守ってなくても、別な同値な確率空間に置き換えればいいことを示唆します。

しかし、“別な同値な確率空間”は、起こり得ないことは削除してしまうことで作っています。この世に絶対に起きない事象はあるけど考えないことにしよう、という態度です。

これは、「月がグリーンチーズからできているという僅かな可能性」「太陽が西から昇る僅かな可能性」も残す発想とは違いますね。

もとのクロムウェルの言葉には、「この世に絶対などない、だから僅かな可能性も考慮すべき」という教訓が含まれている気がします。だとすれば、「起こり得ないことは削除してしまう」は教訓に沿った手法とは言えません。

僕は教訓に沿う気がないから別にいいけどさ。

*1:別な解釈として、 $\Pow(\u{X})$ をシグマ代数とみなして、 $\Sigma_X \subseteq \Pow(\u{X})$ をシグマ代数のあいだの包含だとすることができます。

*2:使っていることは、ゼロ事象の逆像がゼロ事象であることだけです。