型クラスと忘却・追憶構造 - 檜山正幸のキマイラ飼育記 (はてなBlog)

型クラスの多重継承やオーバーロード解決機能を考えるにあたって、「忘却グラフに追憶スパンをアタッチする」という定式化がいいような気がします。それを説明します。

この記事は“とりあえず・取り急ぎ”書いたもので、自己完結的な解説にはなっていません。が、プログラミングに関わるモヤッとした概念を圏論を使って説明する例にはなっているでしょう。$`
\newcommand{\Imp}{\Rightarrow }
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\In}{\text{ in } }
\newcommand{\id}{\mathrm{id} }
\newcommand{\Id}{\mathrm{Id} }
\require{color}
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\Where}{\Keyword{Where } }%
`$

内容：

指標と階層構造
代数構造の階層構造
忘却グラフ
ダイアモンド継承
暗黙の型変換とは
追憶スパン
追憶スパンのアタッチと結合

指標と階層構造

型クラスが提供する機能には、次の3つがあるでしょう。

指標構文
階層化のメカニズム
オーバーロード解決

指標構文の例として、いつも出しているモノイドの定義を挙げます。

signature Monoid {
  sort M
  operation m:M×M → M
  operation e:Unit → M
}

ここで、Unitはユニット型（単元集合の型*1）です。多くのプログラミング言語はモノイドの公理〈法則〉を書けませんが、論理式として公理を書けるなら、指標は次のようになります。

signature Monoid {
  sort M
  operation m:M×M → M
  operation e:Unit → M
laws:
  ∀x, y, z∈M. m(m(x, y), z) = m(x, m(y, z))
  ∀x∈M. m(e(), x) = x
  ∀x∈M. m(x, e()) = x
}

もし、可換図式で公理〈法則〉が書けるプログラミング言語があるなら（ないけど）、モノイドの公理は次のように書けます。

$`\require{AMScd}
\begin{CD}
(M\times M) \times M @>{\alpha_{M, M, M}}>> M\times (M\times M)\\
@V{m\times\id_M}VV @VV{\id_M\times m}V\\
M \times M @. M \times M\\
@V{m}VV @VV{m}V\\
M @= M
\end{CD}\\
\:\\
\begin{CD}
M @>{\lambda_M}>> \mrm{Unit}\times M\\
@| @VV{e\times \id_M}V\\
M @<{m}<< M\times M
\end{CD}\\
\:\\
\begin{CD}
M @>{\rho_M}>> M \times \mrm{Unit}\\
@| @VV{\id_M\times e}V\\
M @<{m}<< M\times M
\end{CD}\\
\:\\
\text{commutative in }{\bf Set}
`$

いずれにしても、指標 Monoid の（集合圏における）モデルの圏としてモノイドの圏が定義できます。

$`
\quad {\bf Monoid} := \mathbb{Model}(\text{Monoid})
`$

ネーミングルールとしては、指標の名前をそのまま太字にして圏の名前とします。通常、モノイドの圏は $`{\bf Mon}`$ と書きますが、このネーミングルールからフルスペルにしています。

モノイドを“継承”して群の定義を書くなら：

signature Group extends Monoid {
  operation s:M → M
laws:
  ∀x∈M. m(x, s(x)) = e()
  ∀x∈M. m(s(x), x) = e()
}

可換モノイド〈アーベル・モノイド〉の定義なら：

signature AbMonoid extends Monoid {
laws:
  ∀x, y∈M. m(x, y) = m(y, x)
}

継承のメカニズムにより、次のような階層構造を作ることができます。

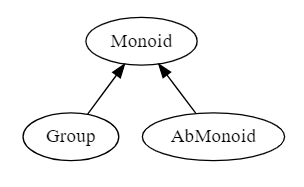
矢印は、下位クラスから上位クラス〈親クラス〉へと向かいます。この矢印は、圏論的には忘却関手と解釈されます。

$`
\quad \mrm{U}_{{\bf Group}, {\bf Monoid}}:{\bf Group} \to {\bf Monoid} \In {\bf CAT}\\
\quad \mrm{U}_{{\bf AbMonoid}, {\bf Monoid}}:{\bf AbMonoid} \to {\bf Monoid} \In {\bf CAT}
`$

代数構造の階層構造

前節で、Monoid, Group, AbMonoid という3つの指標、あるいは $`{\bf Monoid},\, {\bf Group},\, {\bf AbMonoid}`$ という3つの圏のあいだの階層構造を例示しました。圏の階層構造は忘却関手によって与えられます。

代数構造の種類をもう少し増やした例を出しましょう。階層構造は次の有向グラフで示せます。

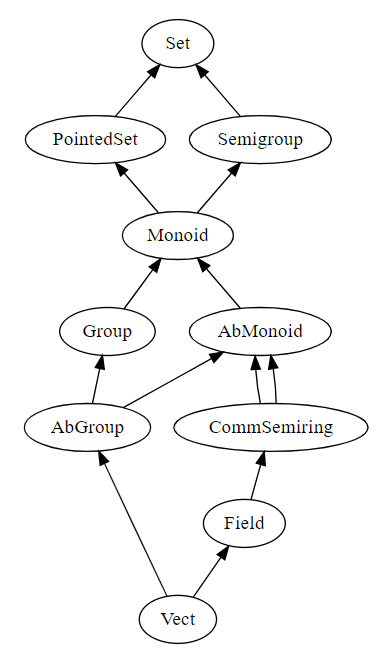
代数構造の名前だけ列挙して、その定義・説明は割愛します。

Set：集合（構造はなし）
PointedSet：付点集合（集合に特定された一点）
Semigroup：半群
Monoid：モノイド
Group：群
AbMonoid：アーベル・モノイド〈可換モノイド〉
AbGroup：アーベル群〈可換群〉
CommSemiring：可換半環
Field：体
Vect：ベクトル空間

指標構文や階層化のメカニズムが何であれ、セマンティクスとしてこのような階層構造が作れればいいわけです。

CommSemiring → AbMonoid の矢印が2本ありますが、これは、可換半環には足し算と掛け算のアーベル・モノイドがあるからです。“足し算のモノイドを取り出す（掛け算は忘れる）”と、“掛け算のモノイドを取り出す（足し算は忘れる）”の2種類の取り出し方（忘れ方）があります。

Vect から出ている2本の矢印で Vect → Field はベクトル空間の係数体〈スカラー体〉を取り出すものです。もう1本の矢印 Vect → AbGroup はベクトル達の足し算のアーベル群を取り出しています。

他の矢印も、構造の一部を取り出す／残りを忘れる行為を表しています。詳細は説明しませんが、常識的な解釈で理解してください。

忘却グラフ

前節の階層構造のグラフは、グラフ理論の意味でのDAG〈Directed Acyclic Graph〉です。サイクルを（もちろん自己ループ辺も）持ちません。有向グラフの2頂点を結ぶ辺が高々1本のとき、グラフは単純〈simple〉といいます。前節のグラフは、CommSemiring → AbMonoid の辺が2本あるので単純ではありません。

$`G`$ はDAGとします。単純である必要はありません。対応 $`D:G \to {\bf CAT}`$ が次の条件を満たすとき忘却グラフ〈forgetful graph〉と呼ぶことにします。

$`G`$ の頂点 $`v`$ に対して $`D(v)`$ は圏（$`{\bf CAT}`$ の対象）である。
$`G`$ の辺 $`e`$ に対して $`D(e)`$ は忘却関手（$`{\bf CAT}`$ の射）である。
頂点に圏、辺に忘却関手の対応は、写像として単射である。

忘却関手は、指標がないと定義できませんが、圏論的には忠実関手と捉えておけばいいでしょう。

前節のグラフは、忘却グラフとみなせます。単なる頂点と辺の図形ではなく、圏と忘却関手としての意味付けをしているからです。

$`D:G\to {\bf CAT}`$ が忘却グラフとします。有向グラフ $`G`$ から生成された自由圏〈パスの圏〉を $`\mathrm{FreeCat}(G)`$ とすると、次の関手が決まります*2。

$`
\quad D^\#:\mathrm{FreeCat}(G) \to {\bf CAT}
`$

この関手の像圏を $`\mrm{Cat}(D)`$ とします。関手 $`D^\#`$ の対象パートは単射だったので、$` |\mrm{Cat}(D)| \cong \mrm{Node}(G)`$ であり、$`\mrm{Cat}(D) \subset {\bf CAT}`$ （部分圏）です。

関手 $`D^\#`$ の対象パートが単射であっても、射パート $`(D^\#)_{\mrm{mor}}: \mrm{Mor}(\mathrm{FreeCat}(G)) \to \mrm{Moe}({\bf CAT})`$ が単射とは限りません。例えば、前節のグラフにおいて、以下の異なる2本のパスは同じ忘却関手にマップされます。

パス Monoid → PointedSet → Set
パス Monoid → Semigroup → Set

上記の例にように、異なるパスが“うまいこと同一視される”と期待しがちですが、そんなにうまくはいきません。

ダイアモンド継承

多重継承の問題点として「ダイアモンド継承の扱い」が挙げられます。困ってしまうということでは問題かも知れませんが、解決策があるわけじゃないです。「ダイアモンド継承が扱いにくい」のは何かの不具合ではなくて、それはそういう構造なのです。

DAG〈Directed Acyclic Graph〉が単純であることを、任意の2頂点を結ぶ辺が高々1本であると定義しました。単純性を圏に対して定義すると、それはやせている〈thin〉という性質になります。任意の2つの対象を結ぶ射が高々1本の圏がやせた圏です。

前々節の代数構造の階層グラフは単純ではありませんが、CommSemigroup → AbMonoid の2本の矢印を一本にすれば単純グラフです。残った矢印は、可換半環の掛け算モノイドを取り出す忘却関手を意味するとします。このように変更した単純DAGを $`G'`$ として、忘却グラフ $`D':G' \to {\bf CAT}`$ を考えます。

$`G'`$ は単純グラフですが、生成された圏 $`\mrm{Cat}(D') \subset {\bf CAT}`$ がやせた圏になるとは限りません。やせた圏では、任意の“射の四角形”は可換四角形になります。$`\mrm{Cat}(D')`$ では可換にならない四角形が存在します。例えば：

$`
\begin{CD}
{\bf Vect} @>{\mrm{U}}>> {\bf AbGroup}\\
@V{\mrm{U}}VV @VV{\mrm{U}}V\\
{\bf CommSemiring} @>{\mrm{U}}>> {\bf AbMonoid}
\end{CD}\\
\:\\
\text{NOT commutative in }{\bf CAT}
`$

すべて $`\mrm{U}`$ でオーバーロードしている忘却関手は、先の忘却グラフを見て解釈してください。

この例から分かることは、忘却グラフの形状である $`G'`$ が単純グラフでも、それから生成される圏がやせているとは限らないことです。直接継承だけでなく間接的な継承まで考えれば、階層構造は圏 $`\mrm{Cat}(D')`$ で与えられます。この圏がやせてないなら、階層構造が順序構造だと考えるわけにはいきません。

おそらく、「階層構造は順序構造だといいなー」という願望があるのでしょう。しかし、その願望は（一般的には）叶わぬことです。構造的に出来ないことを「出来るといいなー」と妄想しても何の意味もありません。

暗黙の型変換とは

オーバーロードや記号の乱用の背後にはある種の“暗黙の型変換”があります。暗黙に変換されてしまうので戸惑うことがあるわけです。オーバーロード／記号の乱用の解決・解釈には、どのように型変換されるかを正確に理解しておく必要があります。

例えば、「自然数型」「$`{\bf N}`$」「Nat」のような言葉や記号がどう解釈されるか？色々な解釈があります。

単なる集合としての自然数型： $`{\bf N}\in |{\bf Set}|`$
順序集合としての自然数型： $`{\bf N}\in |{\bf Ordered}|`$
アーベル・モノイドとしての自然数型： $`{\bf N}\in |{\bf AbMonoid}|`$
可換半環としての自然数型： $`{\bf N}\in |{\bf CommSemiring}|`$

忘却グラフで表されるような、構造や性質が無くなる〈捨てる〉方向の型変換があります。それとは別に、構造や性質が増える〈付け足す〉方向の型変換もあります。例えば、単なる集合としての自然数型を（必要に応じて）アーベル・モノイドとしての自然数型とみなすとかです。

忘却グラフ／忘却関手で表される型変換を忘却・型変換〈forgetful type conversion〉と呼びましょう*3。下位クラスから上位クラス〈親クラス〉に向かう変換です。その反対方向で、上位クラスから下位クラスに向かう型変換、構造や性質が増える型変換を追憶・型変換〈reminiscent type conversion〉と呼ぶことにします*4 -- 比喩的に、忘れた構造・性質を思い起こし再現する変換です。

忘却・型変換は忘却関手で与えられます。では、追憶・型変換は“追憶関手”で与えられるのでしょうか？話はそう単純ではありません。

追憶スパン

忘却関手に対して逆方向の追憶関手があるとすれば、例えば次のようになるでしょう。

$`
\quad \mrm{U}: {\bf AbMonoid} \to {\bf Set} \In {\bf CAT}\\
\quad \mrm{R}: {\bf Set} \to {\bf AbMonoid} \In {\bf CAT}\\
\Where\\
\quad R*U = \Id_{\bf Set}
`$

ここで、'$`*`$' は関手の図式順結合記号で、$`\Id`$ は恒等関手です。今出てきた関手 $`R`$ は、すべての集合にアーベル・モノイド構造を付け足す関手です。そして、すべての写像をアーベル・モノイド間の準同型射に移します。そんな関手、作れるわけないですよね。

追憶関手ではなくて、追憶スパン〈reminiscent span〉を考えます。追憶スパンは、忘却関手に対して定義されます。

$`U:\cat{C} \to \cat{D} \In {\bf CAT}`$ が忘却関手のとき、$`U`$ に対する追憶スパンは次のモノ〈stuff〉から構成されます。

小さい圏 $`\cat{B} \in |{\bf Cat}|`$
関手 $`N:\cat{B} \to \cat{D} \In {\bf CAT}`$
関手 $`S:\cat{B} \to \cat{C} \In {\bf CAT}`$

これらは次の図式で表現できます。

$`\xymatrix{
{} & {\cat{B}} \ar[dl]_{N} \ar[dr]^{S}
& {}
\\
{\cat{D}} & {} & {\cat{C}}
}\\
\text{ in }{\bf CAT}
`$

一般に、この形状の射のペアをスパン〈span〉と呼びます。射（今は実体が関手）$`N`$ がスパンの左脚〈left leg〉、射 $`S`$ がスパンの右脚〈right leg〉です。

さらに、追憶スパンは次の性質を持ちます〈公理を満たします〉。

$`\quad S*U = N : \cat{B} \to \cat{D} \In {\bf CAT}`$

可換図式として描けば：

$`\xymatrix{
{} & {\cat{B}} \ar[dl]_{N} \ar[dr]^{S}
& {}
\\
{\cat{D}} & {} & {\cat{C}} \ar[ll]_{U}
}\\
\text{commutative in }{\bf CAT}
`$

追憶スパンの左脚の関手を名指し関手〈naming functor〉、右脚の関手を選択関手〈selection functor〉と呼ぶことにします。

追憶スパンの実例を挙げましょう。

忘却関手を $`\mathrm{U}: {\bf AbMonoid} \to {\bf Set}\In {\bf CAT}`$ とする。
$`\cat{B}`$ は集合 $`\{1, 2\}`$ とする。（集合は離散圏（恒等射だけを持つ圏）とみなせます。）
$`N:\{1, 2\} \to {\bf Set}`$ は、$`N(1) := {\bf N},\, N(2) := {\bf N}`$ とする。（ここで、$`{\bf N}`$ は単なる集合としての自然数型です。）
$`S:\{1, 2\} \to {\bf Set}`$ は、足し算モノイド、掛け算モノイドとする。
- $`S(1) := ({\bf N}, +, 0)`$
- $`S(2) := ({\bf N}, \times, 1)`$

次のような状況になります。

$`\xymatrix{
{}
&{({\bf N}, +, 0)} \ar@{|->}[ddr]
&{}
&{({\bf N}, \times, 1)\;\in|{\bf AbMonoid}|} \ar@{|->}[ddl]
\\
{1}\ar@{|->}[ru] \ar@{|->}[rrd]
&{}
&{}
&{}
\\
{2}\ar@{|->}[rrruu] \ar@{|->}[rr]
&{}
&{{\bf N}\in |{\bf Set}|}
&{}
}
`$

自然数の集合 $` {\bf N}\in |{\bf Set}|`$ が、番号 1, 2 で名指し〈naming〉されているのは次の理由です。

1 で名指しされた自然数の集合 $`{\bf N}_1 `$ は、足し算モノイド $`({\bf N}, +, 0)`$ の台集合として忘却された結果である。
2 で名指しされた自然数の集合 $`{\bf N}_2 `$ は、掛け算モノイド $`({\bf N}, \times , 1)`$ の台集合として忘却された結果である。
実際には $`{\bf N}_1, {\bf N}_2`$ は同一の集合で、それ自体で“足し算モノイドの台集合”か“掛け算モノイドの台集合”かを区別することはできない。

追憶スパンは、台集合のように忘却の結果である対象（構造や性質の一部を失っている）から、忘却前の構造を特定するメカニズムを与えます。

追憶スパンのアタッチと結合

忘却グラフがあれば、それにより忘却・型変換のメカニズムが与えられます。が、追憶・型変換はサポートされません。忘却グラフ内の特定の辺＝忘却関手に対して、ひとつの追憶スパンを追加すると、その忘却・型変換の逆向きの追憶・型変換がある程度可能となります。「ある程度」と言ったのは、追憶スパンで名指しされている対象に対してしか型変換が出来ないからです。

忘却グラフ内の複数の辺、なんならすべての辺＝忘却関手に追憶スパンをアタッチすることができます。ひとつの辺＝忘却関手に複数の追憶スパンをアタッチしてもかまいませんが、実用上は嬉しくないかも知れません。暗黙の型変換がスムーズにいくようにするには、ひとつの辺＝忘却関手にひとつの追憶スパンでしょう。

さて、次のような状況を考えます。

$`\xymatrix{
{}
& {\cat{B'}} \ar[dl]_{N'} \ar[dr]^{S'}
& {}
& {\cat{B}} \ar[dl]_{N} \ar[dr]^{S}
& {}
\\
{\cat{E}}
& {}
& {\cat{D}} \ar[ll]_{U'}
& {}
& {\cat{C}}\ar[ll]_{U}
}
`$

忘却関手の方向は、

$`
\quad U:\cat{C} \to \cat{D}\\
\quad U':\cat{D} \to \cat{E}
`$

で、追憶スパンの方向は、

$`
\quad (\cat{B}, N, S):\cat{E} \to \cat{D}\\
\quad (\cat{B'}, N', S'):\cat{D} \to \cat{C}
`$

です。忘却関手が結合〈compose〉できるのは明らかですが、追憶スパンは結合できるのでしょうか？

実は結合できます。隣り合ったスパンとスパンが作るコスパン（スパンの双対の形状のペア）がファイバー積〈プルバック〉を持てば、それを利用してスパンの結合が定義可能です。以下の図の菱形の部分がファイバー積になっていれば、外側の大きな三角形が結合した追憶スパンになります。

$`\xymatrix{
{}
& {}
& {\cat{B''}} \ar[dl] \ar[dr]
& {}
& {}
\\
{}
& {\cat{B'}} \ar[dl]_{N'} \ar[dr]^{S'}
& {}
& {\cat{B}} \ar[dl]_{N} \ar[dr]^{S}
& {}
\\
{\cat{E}}
& {}
& {\cat{D}} \ar[ll]_{U'}
& {}
& {\cat{C}}\ar[ll]_{U}
}
`$