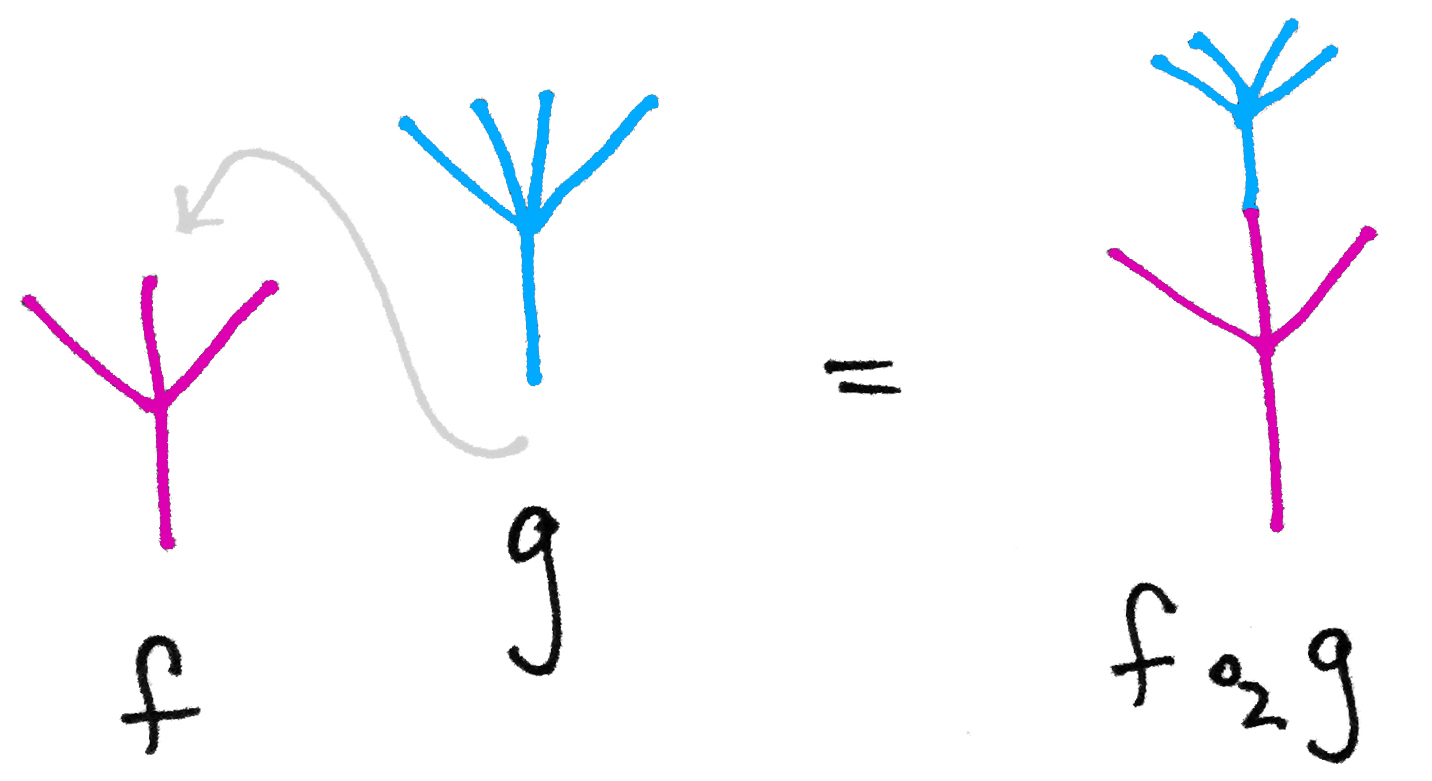型理論、ラムダ計算、論理、形式証明などの話をするときは、表題にあるような基本概念を使いたいのですが、基本概念を説明するほうも/されるほうも消耗しがち、色々と障害があるので。この記事で、なるべく苦労なく手っ取り早く基本概念に馴染めるような説明を試みてみます、正確さは多少犠牲にしますが。
このテの話題は過去にしたことがあるので、関連する記事への参照を適宜はさみます。ただし、予備知識として過去記事が必要ということではありません。詳細や関連事項を知りたい場合に参考にしてください。$`\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\hyp}{\text{-}} %Fullwidth Hyphen-Minus
\newcommand{\mrm}[1]{\mathrm{#1} }
\newcommand{\In}{\text{ in } }
\newcommand{\id}{\mathrm{id} }
\newcommand{\conc}{\mathop{\#} }
\newcommand{\Ev}{\triangleleft }
`$
内容:
多引数関数とタプル1引数関数
$`x, y, z`$ は実数を表す3つの変数だとします。3つの引数を取る関数と、ただ1つの“長さ3のタプル”を引数とする関数は区別しますか? それとも同一視しますか? TypeScriptとLaTeX数式を混ぜた構文で実例を書いてみます。タプル(あるいはリスト)の第$`k`$成分を取り出すことを $`t.k`$ と書いています。
$`\text{function }f (x:{\bf R}, y:{\bf R}, z:{\bf R}) : {\bf R}\:\{\\
\quad \text{return } x^2 + y^2 - z\\
\}\\
\:\\
\text{function }g (t:{\bf R}^3) : {\bf R}\:\{\\
\quad \text{let }x:{\bf R} = t.1\\
\quad \text{let }y:{\bf R} = t.2\\
\quad \text{let }z:{\bf R} = t.3\\
\quad \text{return } x^2 + y^2 - z\\
\}`$
$`f`$ と $`g`$ は、引数の渡し方が違うから違う関数だともいえるし、同じ式 $`x^2 + y^2 - z`$ で定義されるのだから実質同じ関数だともいえます。
まずはとりあえず、違う名前のままで関数のプロファイル(引数と戻り値の仕様)を書いてみます。
$`\quad f:(x:{\bf R}, y:{\bf R}, z:{\bf R}) \to {\bf R}\\
\quad g:(t: {\bf R}^3) \to {\bf R}
`$
これだと、$`f`$ と $`g`$ が“実質的に同じ”という事実は読み取れません。$`f`$ と $`g`$ は厳密に言えば違うだろうが、同じとみなしてもいいのではないか -- こんなとき我々は、オーバーロードとか記号の乱用とか同一視という方法を採用します。
$`\quad f:(x:{\bf R}, y:{\bf R}, z:{\bf R}) \to {\bf R}\\
\quad f:(t: {\bf R}^3) \to {\bf R}
`$
プロファイルは違っていても同じ名前を使うことで、“実質的に同じ”という情報を伝えるわけです。以下では主に、この書き方の約束を使います。注意すべきは「中身が違う関数でもプロファイルが違うから同名でもよい」ではないことです。同じ名前で呼ぶことが許されるのは、プロファイルが違っても“実質的に同じ”ときだけです。
プロファイルに現れる引数変数は省略してもいいとします(引数変数があってもかまいませんが)。
$`\quad f:({\bf R}, {\bf R}, {\bf R}) \to {\bf R}\\
\quad f:({\bf R}^3) \to {\bf R}
`$
ここで重要なことは、$`({\bf R}^3)`$ のような場合でも、囲みの丸括弧を省略しないことです。現実には省略されることが多い(むしろ、ほとんど省略される)のですが、それをやると、いらぬ混乱や誤解が生じることをさんざん経験したので、引数が1個でも0個でも囲み丸括弧は省略しないと約束します。
関連する記事:
デカルト閉圏の複圏
$`\cat{C} = (\cat{C}, \times, {\bf 1}, [\hyp, \hyp])`$ (← 記号の乱用)をデカルト閉圏とします。$`\cat{C}`$ の対象は型、射は関数という解釈をすることにします。$`[\hyp, \hyp]`$ は関数空間型〈アロー型〉を作る型構成子です(射にも働くので反変・共変の双関手ですが)。
圏 $`\cat{C}`$ の射は1引数-1戻り値(1-in 1-out)の関数(のようなもの)なので、n引数-1戻り値(n-in 1-out)の関数達の計算体系として $`\cat{M} = \mrm{Mult}(\cat{C})`$ を考えます。$`\cat{M}`$ はデカルト閉圏 $`\cat{C}`$ の複圏〈multicategory〉と呼びます*1。圏に射があるのと同様に、複圏には複射〈multimorphism〉があります*2。複射のプロファイルは次のように書きます。
$`\quad f:(A_1, \cdots, A_n) \to B \In \cat{M}`$
複射と同じ名前で、$`\cat{C}`$ 内の射も表します。前節と同じ名前の付け方のルールです。
$`\quad f: A_1\times \cdots \times A_n \to B \In \cat{C}`$
プロファイルが、$`(A_1, \cdots, A_n) \to B`$ である $`\cat{M}`$ の複射の集合は $`\cat{M}( (A_1, \cdots, A_n), B)`$ と書き、複ホムセット〈multi-homset〉と呼びます。圏のホムセットのマルチ版です。
$`\quad f:(A_1, \cdots, A_n) \to B \In \cat{M} \iff f \in \cat{M}( (A_1, \cdots, A_n), B)\\
\quad f: A_1\times \cdots\times A_n \to B \In \cat{C} \iff f \in \cat{C}( A_1\times \cdots\times A_n, B)`$
複射にも恒等射があります。
$`\quad \id_A:(A) \to A \In \cat{M} \iff \id_A \in \cat{M}( (A), A)\\
\quad \id_A: A \to A \In \cat{C} \iff \id_A \in \cat{C}( A, A)`$
複写はツリーの形に図示して、その結合〈composition〉は接ぎ木〈grafting〉として描きます(詳細は「モノイド圏上のテンプレート・オペラッド:具体例とソフトウェア的解釈」参照)。
複射 $`f`$ の$`k`$ 番目の枝に $`g`$ を接ぎ木することを、
$`\quad f \circ_k g = g \,;_k f`$
と書きます。
$`\id_A \,;_k f`$ が定義可能なら、これは $`f`$ です(接ぎ木結合の単位律)。テキストで書き下すのは面倒ですが接ぎ木結合の結合律〈associative law〉も成立します。
関連する記事:
複射のパッキング
デカルト閉圏 $`\cat{C}`$ の対象を要素〈項目〉とするリストの集合を $`\mrm{List}(|\cat{C}|)`$ とします。リストの要素をすべてデカルト積〈直積〉する演算を $`\prod`$ で表します*4。
$`\quad \prod : \mrm{List}(|\cat{C}|) \to |\cat{C}| \In {\bf SET}`$ *5
具体的には、
- $`\prod(\, ()\,) = {\bf 1}`$
- $`\prod(\, (A)\,) = A`$
- $`\prod(\, (A_1, A_2)\,) = A_1\times A_2`$
- $`\prod(\, (A_1, A_2, A_3)\,) = (A_1\times A_2) \times A_3`$
- $`\prod(\, (A_1, \cdots , A_{n - 1}, A_n)\,) = \prod(\, (A_1, \cdots, A_{n - 1})\,) \times A_n`$
習慣により*6、$`\mrm{List}(|\cat{C}|)`$ の要素を $`\Gamma, \Phi`$ などのギリシャ文字大文字で表します。ギリシャ文字大文字と総積を表す記号 $`\prod`$ を使うと、次のように書けます。
$`\quad f: \Gamma \to B \In \cat{M} \iff f \in \cat{M}( \Gamma, B)\\
\quad f: \prod( \Gamma ) \to B \In \cat{C} \iff f \in \cat{C}( \prod(\Gamma), B)`$
同じ名前で表している複射と射は1:1の対応があります。この対応〈写像〉を $`\mrm{SrcPack}`$ で表します。
$`\quad \mrm{SrcPack} : \cat{M}(\Gamma, B) \to \cat{C}(\prod(\Gamma), B) \In {\bf SET}`$
同じ名前を使うルール〈オーバーロード・ルール〉は、$`f\in \cat{M}(\Gamma, B)`$ と $`\mrm{SrcPack}(f) \in \cat{C}(\prod(\Gamma), B)`$ を同一視するという約束だったのです。
写像 $`\mrm{SrcPack}`$ は、プロファイルのソース側〈域側〉を総積してターゲット側〈余域側〉はそのままなので、ソース側パック/パッキング〈source-side pack / packing〉、または単にパック/パッキングと呼びます。複圏の複射をパックすると圏の射になります。
写像 $`\mrm{SrcPack}`$ は、正確に言えば、$`\Gamma \in \mrm{List}(|\cat{C}|)`$ と $`B\in |\cat{C}|`$ でインデックス付けられた写像の族
$`\quad (\mrm{SrcPack}_{\Gamma, B})_{\Gamma \in \mrm{List}(|\cat{C}|),B\in |\cat{C}|}`$
です。が、通常はインデックスを省略します。このことは、後で出てくる $`\mrm{FullCurry}, \mrm{TrgPack}, \mrm{Pack}`$ などに関しても同様です。細かい議論をしたいときだけインデックスを付けます。
複射のフルカリー化
複圏 $`\cat{M}`$ の複射のプロファイルは、$`\cat{C}`$ の対象のリスト $`\Gamma`$ と $`\cat{C}`$ の対象 $`A`$ のペア $`(\Gamma, B) \in \mrm{List}(|\cat{C}|) \times |\cat{C}|`$ です。記法の習慣として、区切り記号をカンマではなくて矢印記号にして囲み括弧を付けないだけです。
$`\quad (\Gamma, B) = \Gamma \to B \;\in \mrm{List}(|\cat{C}|) \times |\cat{C}|`$
複射のプロファイルから単一の $`\cat{C}`$ の対象を得る演算 $`\bigwedge`$ を定義しましょう*7。
$`\quad \bigwedge : \mrm{List}(|\cat{C}|)\times |\cat{C}| \to |\cat{C}|`$
リストに対する帰納的定義です。
- $`\bigwedge(\, ()\to B \,) = B`$
- $`\bigwedge(\, (A) \to B \,) = [A, B]`$
- $`\bigwedge(\, (A_1, A_2)\to B \,) = [A_1, [A_2, B] ]`$
- $`\bigwedge(\, (A_1, A_2, A_3) \to B\,) = [A_1, [A_2, [A_3, B] ] ]`$
- $`\bigwedge(\, (A_1, A_2, \cdots , A_n) \to B\,) = [A_1, \bigwedge(\,(A_2, \cdots , A_n) \to B \,) ]`$
デカルト閉圏 $`\cat{C}`$ において、次のホムセット同型(カリー同型)が成立します。
$`\quad \cat{C}(\prod( \Gamma ), B) \cong \cat{C}({\bf 1}, \bigwedge( \Gamma \to B))`$
具体的には:
- $`\cat{C}(\prod(\, () \,), B) \cong \cat{C}({\bf 1}, \bigwedge(\, () \to B \, ))`$ (実際には等号)
- $`\cat{C}(\prod(\, (A) \,), B) \cong \cat{C}({\bf 1}, \bigwedge(\, (A) \to B \, ))`$
- $`\cat{C}(\prod(\, (A_1, A_2) \,), B) \cong \cat{C}({\bf 1}, \bigwedge(\, (A_1, A_2) \to B \, ))`$
- $`\cat{C}(\prod(\, (A_1, A_2, A_3) \,), B) \cong \cat{C}({\bf 1}, \bigwedge(\, (A_1, A_2, A_3) \to B \, ))`$
このホムセット同型と、複射のパッキングを組み合わせたとき、次のような可換図式が成立します。
$`\require{AMScd}
\begin{CD}
\cat{C}(\prod( \Gamma ), B) @>{\mrm{FullCurry}^\cat{C} }>> \cat{C}(\prod(\,() \,), \bigwedge( \Gamma \to B))\\
@A{\mrm{SrcPack}}AA @A{\mrm{SrcPack}}AA\\
\cat{M}( \Gamma, B) @>{\mrm{FullCurry}^\cat{M} }>> \cat{M}(\, (), \bigwedge( \Gamma \to B))
\end{CD}\\
\text{commutative in }{\bf Set}`$
ここで、$`\mrm{FullCurry}^\cat{C}`$ はデカルト閉圏 $`\cat{C}`$ におけるフルカリー化同型写像、$`\mrm{FullCurry}^\cat{M}`$ は対応する複圏 $`\cat{M}`$ におけるフルカリー化同型写像です。
$`\Gamma = (A_1, A_2)`$ のときなら:
$`\require{AMScd}
\begin{CD}
\cat{C}( A_1 \times A_2, B) @>{\mrm{FullCurry}^\cat{C} }>> \cat{C}({\bf 1}, [A_1, [A_2, B] ])\\
@A{\mrm{SrcPack}}AA @A{\mrm{SrcPack}}AA\\
\cat{M}( (A_1, A_2), B) @>{\mrm{FullCurry}^\cat{M} }>> \cat{M}(\, (), [A_1, [A_2, B] ] )
\end{CD}\\
\text{commutative in }{\bf Set}`$
現存する処理系(プログラミング言語、証明支援系)では、$`f`$ と $`\mrm{FullCurry}(f)`$ も同一視することが多いのですが、そうなると、厳密には異なる4つのものを同一視することになり、さすがにワヤクチャになります。$`f`$ のフルカリー化は $`f^\wedge`$ と表すことにします。
- $`f\in \cat{M}( \Gamma, B)`$
- $`\mrm{SrcPack}(f) = f \in \cat{C}(\prod( \Gamma ), B)`$
- $`\mrm{FullCurry}^\cat{M}(f) = f^\wedge \in \cat{M}(\, (), \bigwedge( \Gamma \to B))`$
- $`\mrm{FullCurry}^\cat{C}(\mrm{SrcPack}(f) ) = \mrm{FullCurry}^\cat{C}(f) = f^\wedge \in \cat{C}( \prod(\,() \,), \bigwedge( \Gamma \to B))`$
あるいは次のようにも書けます。
- $`f:\Gamma \to B \In \cat{M}`$
- $`f: \prod(\Gamma) \to B \In \cat{C}`$
- $`f^\wedge: () \to \bigwedge(\Gamma \to B) \In \cat{M}`$
- $`f^\wedge : {\bf 1} \to \bigwedge(\Gamma \to B) \In \cat{C}`$
関連する記事:
複圏、圏、型システム
複圏の複射 $`f`$ と対応するパックされた射 $`\mrm{SrcPack}(f)`$ を同一視する約束でした。が、区別したほうが都合がいい場面もあります。その場合は、
$`\quad {^\pi f} := \mrm{SrcPack}(f)`$
という記法を使いましょう。左肩に添え字の $`\pi`$ を付けます。
- $`f:\Gamma \to B \In \cat{M}`$
- $`{^\pi f}: \prod(\Gamma) \to B \In \cat{C}`$
- $`f^\wedge: () \to \bigwedge(\Gamma \to B) \In \cat{M}`$
- $`{^\pi f}^\wedge : {\bf 1} \to \bigwedge(\Gamma \to B) \In \cat{C}`$
関数型プログラミング言語におけるg: A -> Bのような宣言(Haskellならコロン2つ)は、デカルト閉圏の射のプロファイル $`g: A \to B \In \cat{C}`$ とは対応しません。g: A -> B のデカルト閉圏における解釈〈意味論〉は、
$`\quad g : {\bf 1} \to [A, B] \In \cat{C}`$
です。
g: A -> Bは、デカルト閉圏 $`\cat{C}`$ から作られた型システムを $`/\cat{C}/`$ と置いて*8、その型システムにおける宣言と解釈できます。
$`\quad g : {\bf 1} \to [A, B] \In \cat{C} \iff g : A \to B \In /\cat{C}/`$
この節では、オーバーロード/同一視をしない記法を紹介したのですが、現存する処理系やその説明では、これらすべてがオーバーロード/同一視される可能性があります。厳密に言えば違うモノが、同じ名前で呼ばれるのです。$`\Gamma = (A_1, A_2, \cdots, A_n)`$ として:
- $`f: \Gamma \to B \In \cat{M}`$ (もとの複射)
- $`f: \prod(\Gamma) \to B \In \cat{C}`$ (複射からパックされた射)
- $`f: () \to \bigwedge(\Gamma \to B) \In \cat{M}`$ (フルカリー化された複射)
- $`f : {\bf 1} \to \bigwedge(\Gamma \to B) \In \cat{C}`$ (フルカリー化された複射からパックされた射)
- $`f : A_1 \to \cdots \to A_n \to B \In /\cat{C}/`$ (型システムにおける宣言)
$`\Gamma = (A_1, A_2)`$ のときなら:
- $`f: (A_1, A_2) \to B \In \cat{M}`$ (もとの複射)
- $`f: A_1\times A_2 \to B \In \cat{C}`$ (複射からパックされた射)
- $`f: () \to [A_1, [A_2, B] ] \In \cat{M}`$ (フルカリー化された複射)
- $`f : {\bf 1} \to [A_2, [A_1, B] ] \In \cat{C}`$ (フルカリー化された複射からパックされた射)
- $`f : A_1 \to A_2 \to B \In /\cat{C}/`$ (型システムにおける宣言)
オーバーロード/同一視は、いちいち区別することによる煩雑さを避ける配慮なのかも知れませんが、過剰なオーバーロード/同一視が全体の構造をワケワカラナクしていることがあります。煩雑であっても、その煩雑さが事実であり現象でありメカニズムなのです。事実・現象・メカニズムを曖昧にして得られた簡潔さはマヤカシです。
関連する記事:
デカルト閉圏の多圏
圏 $`\cat{C}`$ の射が関数(1-in 1-out)だとするなら、複圏 $`\cat{M} = \mrm{Mult}(\cat{C})`$ の複射は多引数関数(n-in 1-out)でした。となると、戻り値も複数ある多値多引数関数(n-in m-out)も考えるのは自然な流れでしょう。
$`\Gamma = (A_1, \cdots, A_n)`$ と $`\Phi = (B_1, \cdots, B_m)`$ を、$`\cat{C}`$ の対象を要素とするリストだとして、多値多引数関数(のようなもの)のプロファイルは次のように書けます。
$`\quad \Gamma \to \Phi`$
あるいは、
$`\quad (A_1, \cdots, A_n) \to (B_1, \cdots, B_m)`$
先に説明した理由により、リストの囲み丸括弧は省略しません。
多値多引数関数の抽象化を多射〈polymorphism*9〉と呼びます。多射の集まりである計算体系を多圏〈polycategory〉と呼びます。ここで考える多圏は、デカルト閉圏 $`\cat{C}`$ から作られた $`\cat{P} = \mrm{Poly}(\cat{C})`$ に限ります。
複圏の場合と同様に、多圏の多ホムセット〈poly-homset〉$`\cat{P}(\Gamma, \Phi)`$ を定義できます。
$`\quad f: \Gamma \to \Phi \In \cat{P} \iff f \in \cat{P}(\Gamma, \Phi)`$
あるいは、
$`\quad f: (A_1, \cdots, A_n) \to (B_1, \cdots, B_m) \In \cat{P} \\
\qquad \iff f \in \cat{P}( (A_1, \cdots, A_n), (B_1, \cdots, B_m) )`$
多ホムセット $`\cat{P}(\Gamma, \Phi)`$ と複ホムセット $`\cat{M}(\Gamma, \prod(\Phi))`$ とホムセット $`\cat{C}(\prod(\Gamma), \prod(\Phi))`$ は1:1対応します。対応する多射、複射、射を同じ名前で呼ぶことにします。
- $`f: \Gamma \to \Phi \In \cat{P}`$
- $`f: \Gamma \to \prod(\Phi) \In \cat{M}`$
- $`f: \prod(\Gamma) \to \prod(\Phi) \In \cat{C}`$
$`\Gamma = (A_1, A_2), \Phi = (B_1, B_2)`$ の場合ならば:
- $`f: (A_1, A_2) \to (B_1, B_2) \In \cat{P}`$
- $`f: (A_1, A_2) \to B_1\times B_2 \In \cat{M}`$
- $`f: A_1\times A_2 \to B_1\times B_2 \In \cat{C}`$
恒等多射、恒等複射、恒等射は次のようです。
- $`\id_A : (A) \to (A) \In \cat{P}`$
- $`\id_A : (A) \to A \In \cat{M}`$
- $`\id_A : A \to A \In \cat{C}`$
どれも $`\id_A`$ と書きますがプロファイルは区別します。この区別のために、囲み括弧の省略を禁止したのです。
多圏の多射、複圏の複射、圏の射の同一視(同じ名前)の根拠となる写像は次の $`\mrm{TrgPack}, \mrm{Pack}`$ です。
$`\begin{CD}
\cat{P}(\Gamma, \Phi) @>{\mrm{TrgPack}}>> \cat{M}(\Gamma, \prod(\Phi))\\
@V{ \mrm{Pack} }VV @|\\
\cat{C}(\prod(\Gamma), \prod(\Phi)) @<{\mrm{SrcPack}}<< \cat{M}(\Gamma, \prod(\Phi))
\end{CD}\\
\text{commutative in }{\bf Set}`$
$`\mrm{TrgPack}`$ を多射のターゲット側パック/パッキング〈target-side pack / packing〉、$`\mrm{Pack}`$ を多射の両側パック/パッキング〈two-side pack / packing〉と呼びます。文脈から事情が明らかなら、単にパック/パッキングでもかまいません。多圏の多射をターゲット側パックすると複圏の複射になります。多圏の多射を両側パックすると圏の射になります。
$`\Gamma = (A_1, A_2), \Phi = (B_1, B_2)`$ の場合のパッキングは次のようです。
$`\begin{CD}
\cat{P}( (A_1, A_2), (B_1, B_2)) @>{\mrm{TrgPack}}>> \cat{M}( (A_1, A_2), B_1\times B_2)\\
@V{ \mrm{Pack} }VV @|\\
\cat{C}(A_1\times A_2, B_1 \times B_2 ) @<{\mrm{SrcPack}}<< \cat{M}( (A_1, A_2), B_1\times B_2)
\end{CD}\\
\text{commutative in }{\bf Set}`$
2つの多射は、様々な方法で結合〈composition〉できます。これは複雑になるので、結合の方法や法則をテキストで(文字・記号ベースで)記述するのは面倒な作業になります。ストリング図で記述すれば直感的なんだけどね(「証明と計算は同じこと: 形式証明におけるノードとコネクター」参照)。
プログラミング言語(のソースコード)はテキストで書くので、多値関数の記述は面倒で難しくなります。(おそらく)そのため、プログラミング言語では多値関数は人気がありません。しかし、形式証明の記述では、多圏の多射を使うほうが自然で分かりやすい記述ができます。
関連する記事:
- 多値関数関連:自家製まとめリンク集
- 自然演繹はちっとも自然じゃない -- 圏論による再考
- 多圏の必要性、煩雑さ、そして単純化
- 対称モノイド多圏(簡約版)
- 簡約多圏とシーケント計算
- 述語論理: 様々な多圏達の分類整理
- 証明と計算は同じこと: 形式証明におけるノードとコネクター
多圏をモノイド圏とみなす
多圏における多射の結合は、ストリング図ならワイヤーを引き回して繋ぐことに対応します。様々なワイヤリングがありますが、次のルールによる結合なら単純です。
- 複射 $`f: \Gamma \to \Phi`$ と複射 $`g: \Theta \to \Psi`$ は、$`\Phi = \Theta`$ のときだけ結合可能とする。
- $`\cat{P}`$ における複射の結合と、対応する射の結合($`\cat{C}`$ における結合)が対応するようにする。
上記のような多射の結合を $`f;g`$ と書くことにします。対象のリスト $`\Gamma`$ に対する恒等射 $`\id_\Gamma`$ も定義できて、多圏 $`\cat{P}`$ は通常の圏とみなせます。
そればかりではなくて、リストの連接〈concatenation〉演算を $`\conc`$ とすると、$`(\cat{P}, \conc, ())`$ は連接をモノイド積とするモノイド圏になります。このモノイド圏は、もとのデカルト積をモノイド積とするモノイド圏 $`(\cat{C}, \times, {\bf 1})`$ とほぼ同じです。正確に言えば、$`(\cat{P}, \conc, ())`$ と $`(\cat{C}, \times, {\bf 1})`$ はモノイド圏として同値な圏です*10。
もとのデカルト閉圏 $`\cat{C}`$ をそのまま使うより、リストを対象としてリストの連接をモノイド積とするモノイド圏 $`(\cat{P}, \conc, () )`$ のほうが計算や図示には便利です。無意識のうちに、$`\cat{C}`$ の代わりに $`(\cat{P}, \conc, () )`$ を使っていることが多いと思います。
さて、ひとつのデカルト閉圏 $`\cat{C}`$ からの派生物として、次のような構造が作れました。
- 複圏 $`\cat{M} = \mrm{Mult}(\cat{C})`$
- 型システム $`/\cat{C}/`$
- 多圏 $`\cat{P} = \mrm{Poly}(\cat{C})`$
- モノイド圏 $`(\cat{P}, \conc, () )`$
これらの構造は、互いに密接に関連しているし、ときに同一視されます。しかし、何の区別もせずにグチャグチャなままにしておくと、ワヤクチャ・ワケワカランな状況になります。
関連する記事:
コンビネータ
デカルト圏の基本的な射である対称射〈スワップ〉$`\sigma_{A, B}`$ 、終射〈破棄射 | 削除射〉$`!_A`$ 、対角射〈コピー射〉$`\Delta_A`$ を多圏 $`\cat{P} = \mrm{Poly}(\cat{C})`$ 内で考えてみると、次のプロファイルを持ちます。
- $`\sigma_{A, B}: (A, B) \to (B, A) \In \cat{P}`$
- $`!_A: (A) \to () \In \cat{P}`$
- $`\Delta_A: (A) \to (A, A) \In \cat{P}`$
複圏 $`\cat{M} = \mrm{Mult}(\cat{C})`$ に移してフルカリー化すると:
- $`{\sigma_{A, B}}^\wedge: () \to [A, [B, B\times A]] \In \cat{M}`$
- $`{!_A }^\wedge: () \to [A, {\bf 1}] \In \cat{M}`$
- $`{\Delta_A }^\wedge: () \to [A, A\times A] \In \cat{M}`$
型システム $`/\cat{C}/`$ における宣言で書けば:
- $`{\sigma_{A, B}}^\wedge: A \to B \to B\times A \In /\cat{C}/`$
- $`{!_A }^\wedge: A \to {\bf 1} \In /\cat{C}/`$
- $`{\Delta_A }^\wedge: A \to A\times A \In /\cat{C}/`$
だいぶ印象は変わります(ストリング図で描くとだいぶ違った図形です)。しかし、射/複射/多射を記述していることに変わりはありません。なので、“意図的に混同”することは(好ましくはないけど)許されるでしょう。「意図的に混同」とは事情を知った上で、煩雑さを避けるためにオーバーロード/同一視を行うということです。
さてところで、コンビネータ〈combinator〉(あるいはオペレータ〈operator〉とは、射/複射/多射ではなくて、ホムセット/複ホムセット/多ホムセットに働く写像のことです。コンビネータは射とは別物です。射とコンビネータを混同するのは(意図的であっても)良くないと僕は思います。
しかし困ったことには(素晴らしいことかも知れないが)、デカルト閉圏の指数〈内部ホム〉機能を使うと、ホムセット/複ホムセット/多ホムセットを対象とみなすことができるので、コンビネータと射(あるいは複射/多射)の混同・同一視は容易にできます。プログラミング言語や証明支援系では、この混同・同一視が利用されてもいます。
射とコンビネータの混同・同一視の功罪はいったん棚上げにして、コンビネータの具体例を挙げます。
デカルト圏 $`\cat{C}`$ では、次のようなデカルト・ペアリングが可能です。
$`\quad \langle\hyp, \hyp\rangle : \cat{C}(X, A)\times \cat{C}(X, B) \to \cat{C}(X, A\times B) \In {\bf Set}`$
より具体的に書けば:
$`\text{for }f \in \cat{C}(X, A)\\
\text{for }g \in \cat{C}(X, B)\\
\quad \langle f, g \rangle \in \cat{C}(X, A\times B)`$
この二項演算 $`\langle\hyp, \hyp\rangle`$ は、実際には
$`\quad (\langle\hyp, \hyp\rangle_{X, A, B})_{X, A, B\in |\cat{C}|}`$
とインデックスされた写像の族です。明らかに、$`\cat{C}`$ 内に居る射とは別物だという感じがするでしょう。
デカルト圏 $`\cat{C}`$ がデカルト閉で、$`\cat{C}`$ のホムセットへの作用を内部化〈レイフィケーション〉できるとすると、コンビネータであるデカルト・ペアリングも次のように内部化できます。
- $`\langle\hyp, \hyp\rangle : [X, A]\times [X, B] \to [X, A\times B] \In \cat{C}`$
- $`\langle\hyp, \hyp\rangle^\wedge : {\bf 1} \to [ [X, A], [ [X, B] , [X, A\times B] ] ]\In \cat{C}`$
- $`\langle\hyp, \hyp\rangle^\wedge : (X \to A) \to (X \to B) \to X \to A\times B \In /\cat{C}/`$
僕の気持ちとしては、内部化された $`\langle\hyp, \hyp\rangle^\wedge`$ は、あくまでコンビネータをエンコードしたものであって、コンビネータとして扱って欲しくはない、ということです。これは、メンタルな問題かも知れないので、強くは主張しませんが。
もうひとつコンビネータの事例として、外部化された評価〈eval〉を挙げます。
デカルト閉圏の評価射 $`\mrm{ev}_{A, B}: [A, B]\times A \to B`$ は圏 $`\cat{C}`$ 内の射ですが、評価射を外部化した二項演算を次のように定義できます。
$`\quad (\hyp \Ev^X_{A, B} \hyp) : \cat{C}(X, [A, B])\times \cat{C}(X, A) \to \cat{C}(X, B) \In {\bf Set}\\
\:\\
\text{for }f \in \cat{C}(X, [A, B])\\
\text{for }a \in \cat{C}(X, A)\\
\quad f \Ev a := \mrm{ev}\circ \langle f, a\rangle \in \cat{C}(X, B)`$
特に $`X = {\bf 1}`$ と置くと次の演算〈コンビネータ〉になります。
$`\quad (\hyp \Ev^{\bf 1}_{A, B} \hyp) : \cat{C}({\bf 1}, [A, B])\times \cat{C}({\bf 1}, A) \to \cat{C}({\bf 1}, B) \In {\bf Set}`$
コンビネータ $`\Ev^{\bf 1}_{A, B}`$ は射 $`\mrm{ev}_{A, B}`$ を外延化(「デカルト閉・型システム」参照)したものですが、この2つの区別は微妙かも知れません。
関連する記事:
区別したいときは
前節で述べた評価射 $`\mrm{ev}`$ は、論理のモーダスポネンスに相当するものです。評価射を外部化したコンビネータ $`\Ev`$ は、含意導入の推論規則に相当します。カリー/ハワード/ランベック対応〈Curry-Howard-Lambek correspondence〉により、論理とラムダ計算は対応しますが、ラムダ計算が棲んでいる生息地〈habitat〉が色々とあり得ます。
様々な評価射とそのコンビネータを区別したいなら、プロファイルをシッカリ書いて、識別のための添字を付けるとかします。
- $`{\mrm{ev}^\cat{C}}_{A, B}: [A,B]\times A \to B \In \cat{C}`$
- $`{\mrm{ev}^\cat{M}}_{A, B}: ([A,B], A) \to B \In \cat{M}`$
- $`{\mrm{ev}^\cat{P}}_{A, B}: ([A,B], A) \to (B) \In \cat{P}`$
- $`{\Ev^\cat{C}}^X_{A, B} : \cat{C}(X, [A, B])\times \cat{C}(X, A) \to \cat{C}(X, B) \In {\bf Set}`$
- $`{\Ev^\cat{M}}^\Gamma_{A, B} : \cat{M}(\Gamma, [A, B])\times \cat{M}(\Gamma, A) \to \cat{M}(\Gamma, B) \In {\bf Set}`$
- $`{\Ev^\cat{P}}^\Gamma_{A, B} : \cat{P}(\Gamma, ([A, B]) )\times \cat{P}(\Gamma, (A) ) \to \cat{P}(\Gamma, (B) ) \In {\bf Set}`$
多圏 $`\cat{P}`$ だと、次のようなコンビネータも考えられます。
- $`{\Ev^\cat{P}}^\Gamma_{A, B} : \cat{P}(\Gamma, ([A, B], A) ) \to \cat{P}(\Gamma, (B) ) \In {\bf Set}`$
ある概念に対する定式化の候補がたくさんあるのです。
いちいち区別するのが面倒になったら、どの候補を選んでも同様な議論が出来ることに納得したら、そのときは“意図的な混同”をしてもいいと思います。
関連する記事:
おわりに
ラムダ計算や論理をデカルト閉圏 $`\cat{C}`$ を意味領域として展開するときは、複圏 $`\cat{M} = \mrm{Mult}(\cat{C})`$ と多圏 $`\cat{P} = \mrm{Poly}(\cat{C})`$ も一緒に考えた複合構造物のなかで作業すると、計算も描画も捗ってたいへん便利です。
便利さの代償として、ある程度の複雑さ・煩雑さは受け入れなくてはなりません。複合構造物のなかでは、カリー化、パッキング、内部化〈レイフィケーション〉などが縦横無尽に働くので、ひとつの概念に多様な表現が存在します。選択肢が多いことは負担にもなりますが、その多様さ/柔軟さを活かした議論も可能となります。
*1:デカルト閉圏とは独立に複圏〈オペラッド〉の定義はありますが、ここでは、デカルト閉圏から作られた複圏だけを考えます。デカルト閉圏、より一般にはモノイド閉圏には、計算デバイスとしての複圏と多圏を付随させて考えたほうが便利です。「対称モノイド多圏(簡約版)」参照。
*2:複圏をオペラッド〈operad〉、複射をオペレータ〈operator〉/オペレーション〈operation〉ということもあります。
*3:画像は https://uploads-ssl.webflow.com/5b1d427ae0c922e912eda447/5b58d15cd283c6d6bc7522b4_2.jpg より
*4:記号 $`\prod`$ はパイ型/パイ構成と同じですが、総積を取る点では同じですから、記号がかぶるのは問題ないでしょう。
*5:デカルト閉圏 $`\cat{C}`$ (の台圏)が小さいとは仮定してません。なので、$`|\cat{C}|`$ は大きい集合になる可能性があります。よって、写像 $`\prod`$ は大きい集合も含む集合圏 $`{\bf SET}`$ 内で考える必要があります。
*6:圏論よりは、論理や型理論の習慣です。
*7:「自然言語前提の証明記述でも形式的枠組みは必要」では、 $`[\Gamma \mathrel{\triangleright\!\!\longrightarrow} P]`$ という書き方をしています。が、ブラケットは他の用途でも使うので、ここでは $`\bigwedge`$ を使うことにします。$`\bigwedge`$ の他の用法とのコンフリクトのリスクはありますが、それはもう致し方ない。
*8:$`/\cat{C}/`$ は、$`\cat{C}`$ 自身で豊穣化された豊穣圏とみなせます。「豊饒圏(ピノキオ)が圏(人間)になる物語」参照。
*9:英語のpolymorphismは多相の意味のポリモーフィズムとかぶるので、polyarrow, polyarrowがよく使われます。
*10:モノイド圏 $`(\cat{P}, \conc, () )`$ は、モノイド圏 $`(\cat{C}, \times, {\bf 1})`$ の厳密化〈strictification〉になっています。「ツリー書き換え系とマックレーンの一貫性定理」を参照してください。