半グラフ変形とDead-Or-Alive構造 - 檜山正幸のキマイラ飼育記 (はてなBlog)

半グラフとその変形を理解したいと思っているわけですが、その手段として、半グラフ上のDead-Or-Alive構造が有効そうです。Dead-Or-Alive構造が何であるかは本文で述べるとして、注目すべきことは、半グラフ $`\alpha`$ をとると、その上のDead-Or-Alive構造の全体 $`\mathrm{DOA}(\alpha)`$ が有限集合であることです。有限集合 $`\mathrm{DOA}(\alpha)`$ は、半グラフ $`\alpha`$ をソース〈域〉とする半グラフ架橋・縮減変形（これも本文内で定義）の同型類を尽くしています。

$`\mathrm{DOA}(\alpha)`$ により、半グラフ $`\alpha`$ からの半グラフ架橋・縮減変形を有限的・具体的に記述できることになります。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\In}{\text{ in } }
\newcommand{\bdry}{\partial }
\newcommand{\Imp}{\Rightarrow }
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\slt}{\mathrel{\dot{\lt}}}% successor lt
\newcommand{\pto}{\not\to }% pro arrow
`$

内容：

半グラフ架橋・縮減変形
半グラフに関する用語・記法
半グラフ上のDead-Or-Alive構造
DOA構造の条件
DOA構造から作られる各種半グラフ
頂点同一視関係と頂点マージ変形
DOA構造と半グラフ変形

半グラフ架橋・縮減変形

「半グラフの二重圏と半グラフ変形」で述べたように、半グラフ変形〈semi-graph deformation〉は、次の基本変形の組み合わせになります。

切断〈cutting〉：内部辺を2本の外部辺に分解
架橋〈bridging〉： 2本の外部辺から1本の内部辺を作る
実縮減〈actual shrinking〉：内部辺の両端を同一視して内部辺を消去
仮想縮減〈virtual shrinking〉： 2本の外部辺の2つの端点〈境界点〉を同一視して2本の外部辺を消去
上記の“辺に対する操作”と協調する頂点同一視（後述）

このなかで、切断を使わずに、架橋と縮減（実縮減と仮想縮減）と頂点同一視から構成された半グラフ変形を半グラフ架橋・縮減変形〈semigraph bridging-shrinking deformation〉と呼ぶことにします。

切断は扱いにくい面があるので、架橋・縮減変形だけを考えることは理にかなっています。ボリソフ／マニン〈D. Borisov, Yu. I. Manin〉、コステロ〈Kevin Costello〉、バーガー／カウフマン〈Clemens Berger, Ralph M. Kaufmann〉などが扱っている半グラフ変形は架橋・縮減変形です。

ここでは、半グラフ架橋・縮減変形を直接扱う代わりに、半グラフ $`\alpha`$ に対して、$`\alpha`$ 上のDead-Or-Alive構造〈DOA構造〉 $`\phi`$ （定義は後述）を考えます。DOA構造 $`\phi`$ から、ボリソフ／マニンの意味の半グラフ変形（ボリソフ／マニンは morphism of graphs と呼んでますが） $`\mrm{BMDefm}(\phi)`$ を定義できます。

$`\quad \mrm{BMDefm}(\phi) : \alpha \pto \mrm{Trg}(\phi) \In {\bf SemiGraphDC}`$

ボリソフ／マニンの意味の半グラフ変形は、半グラフの二重圏のプロ射〈横1-射〉とみなします（「半グラフの二重圏と半グラフ変形」参照）。$`\mrm{Trg}(\phi)`$ は、DOA構造から一意的にきまるターゲット半グラフです。

半グラフに関する用語・記法

用語・記法を今までとは若干変えます。

半辺〈half-edge〉の代わりにフラグ〈flag〉を使います。変更の理由は、半辺と辺、半辺と外部辺が混同されないように、「辺」と似てない言葉にしたいからです。

半グラフ $`\alpha`$ は、頂点の集合とフラグの集合を持ちます。

$`V(\alpha)`$ ：半グラフ $`\alpha`$ の頂点の集合
$`F(\alpha)`$ ：半グラフ $`\alpha`$ のフラグの集合

フラグには唯一の端点〈境界点〉があります。フラグに境界点を対応させる写像が $`\bdry_\alpha`$ です。

$`\quad \bdry_\alpha : F(\alpha) \to V(\alpha) \In {\bf Set}`$

パートナー指定対合〈partner designation involution〉はペアリング対合〈pairing involution〉とも呼びます。ペアリング対合は不動点を許すので、“一人だけのペア”も存在します。

半グラフ $`\alpha`$ は、上記の構成素を並べて次のように書きます。

$`\quad \alpha = (V(\alpha), F(\alpha), \bdry_\alpha, \iota_\alpha)`$

半グラフ $`\alpha`$ のフラグの集合 $`F(\alpha)`$ 上にペアリング対合 $`\iota_\alpha`$ が働きますが、$`\iota_\alpha`$ （が誘導する同値関係）による商集合を辺〈edge〉の集合と呼びます。

$`\quad E(\alpha) := F(\alpha)/\iota_\alpha \\
\quad \pi_\alpha : F(\alpha) \to E(\alpha) \text{ (標準射影)}
`$

辺の集合を2つの部分に分けます。

$`\quad \mrm{Ext}E(\alpha) := \{e \in E(\alpha) \mid e \text{ は単元元集合}\}\\
\quad \mrm{Int}E(\alpha) := \{e \in E(\alpha) \mid e \text{ は二元集合}\}
`$

さらに次の定義をします。

$`\quad \mrm{Tail}(\alpha) := \{f \in F(\alpha)\mid \iota_\alpha(f) = f \}\\
\quad \mrm{Body}(\alpha) := \{f \in F(\alpha)\mid \iota_\alpha(f) \ne f \}
`$

$`\pi_\alpha : F(\alpha) \to E(\alpha)`$ で次のように対応します。

$`\quad (\pi_\alpha)_*(\mrm{Tail}(\alpha)) = \mrm{Ext}E(\alpha)\\
\quad (\pi_\alpha)_*(\mrm{Body}(\alpha)) = \mrm{Int}E(\alpha)
`$

次の呼び名を使います。

$`\mrm{Ext}E(\alpha)`$ の要素： 外部辺〈external edge〉
$`\mrm{Int}E(\alpha)`$ の要素： 内部辺〈internal edge〉
$`\mrm{Tail}(\alpha)`$ の要素： テールフラグ〈tail flag〉
$`\mrm{Body}(\alpha)`$ の要素： ボディフラグ〈body flag〉

単一のテールフラグからなる単元集合が外部辺で、2つのボディフラグのペア〈二元集合〉が内部辺です。

[補足]
ボリソフ／マニンやバーガー／カウフマンは、内部辺のみを辺と呼び、外部辺とテールフラグを同一視しているようです。つまり、「内部辺／外部辺」の代わりに「辺／テール」を使うわけです。この方式は、概念的にバランスが悪い気がするので、フラグと辺はまったく別物としました。
[/補足]

半グラフ上のDead-Or-Alive構造

$`\alpha`$ が半グラフとして、$`\alpha`$ 上のDead-Or-Alive構造〈DOA構造 | Dead-Or-Alive structure〉$`\phi`$ は次の構成素からなります。

$`\mrm{Dead}(\phi)\subseteq F(\alpha)`$ ： $`\phi`$ の亡骸〈なきがら〉フラグ〈dead flag〉の集合
$`\mrm{Alive}(\phi)\subseteq F(\alpha)`$ ： $`\phi`$ の生存フラグ〈alive flag〉の集合
$`\iota_\phi : F(\alpha) \to F(\alpha)`$ ： $`\phi`$ のペアリング対合〈pairing involution〉
$`\sim_\phi`$ ： $`V(\alpha)`$ 上の同値関係。頂点同一視関係〈vertex identification relation〉（Vertex identification 参照）と呼ぶ。

これらの構成素がDOA構造であるためには、後述の幾つかの条件が付きます。半グラフ $`\alpha`$ 上のDOA構造 $`\phi`$ を次のように書きます。

$`\quad \phi = \phi/\alpha = (\mrm{Dead}(\phi), \mrm{Alive}(\phi), \iota_\phi, \sim_\phi)/\alpha`$

$`\phi/\alpha`$ は商集合ではなくて、$`\phi \text{ over }\alpha`$ という意味です。

DOA構造の条件〈公理〉を述べる前に、DOA構造が何のためにあるのか、どう使うかを説明します。半グラフ $`\alpha`$ 上のDOA構造 $`\phi/\alpha`$ は、$`\alpha`$ からもうひとつの半グラフ $`\beta`$ への架橋・縮減変形を決定します。架橋・縮減変形のターゲット〈余域〉である $`\beta`$ は $`\phi/\alpha`$ から構成できます。

$`\quad V(\beta) := V(\alpha)/\!\sim_\phi\\
\quad F(\beta) := \mrm{Alive}(\phi)
`$

その他の $`\beta`$ の構成素も容易に $`\phi/\alpha`$ から定義できます（後述）。

半グラフ $`\beta`$ のフラグは $`\mrm{Alive}(\phi)`$ が使われ、$`\mrm{Dead}(\phi)`$ は消去されます。つまり、生存フラグはターゲット側に生き残り、亡骸フラグは捨てられます。架橋・縮減変形は、ソース側のフラグの一部（生存フラグ達）を使って新しい半グラフを生成する操作です。

記法を簡略にするために、$`\alpha = (V, F, \bdry, \iota)`$ と書きます。次の定義をします。

$`\quad V' := V/\!\sim_\phi\\
\quad p_\phi : V \to V/\!\sim_\phi \text{ (商集合への標準射影)}\\
\quad \bdry' := \bdry\,; p_\phi : F \to V'
`$

DOA構造の条件は色々あるので次節で述べます。

DOA構造の条件

まず、$`\alpha`$ のフラグは亡骸か生存のどちらかに必ず分類されます。

$`\quad \mrm{Dead}(\phi) \cup \mrm{Alive}(\phi) = F\\
\quad \mrm{Dead}(\phi) \cap \mrm{Alive}(\phi) = \emptyset
`$

$`\alpha`$ のペアリング対合は、$`\mrm{Dead}(\phi), \mrm{Alive}(\phi)`$ に対して閉じています。次が成立することです。

$`\quad \iota_*(\mrm{Dead}(\phi)) \subseteq \mrm{Dead}(\phi)\\
\quad \iota_*(\mrm{Alive}(\phi)) \subseteq \mrm{Alive}(\phi)
`$

したがって、$`\iota`$ を制限した写像が、$`\mrm{Dead}(\phi), \mrm{Alive}(\phi)`$ に対する対合になります。

$`\quad \iota|_{\mrm{Dead}(\phi)} : \mrm{Dead}(\phi) \to \mrm{Dead}(\phi) \text{ (対合)}\\
\quad \iota|_{\mrm{Alive}(\phi)} : \mrm{Alive}(\phi) \to \mrm{Alive}(\phi) \text{ (対合)}
`$

$`\phi`$ のペアリング対合（$`\alpha`$ のペアリング対合とは別）も同様な性質を持ちます。

$`\quad \iota_\phi|_{\mrm{Dead}(\phi)} : \mrm{Dead}(\phi) \to \mrm{Dead}(\phi) \text{ (対合)}\\
\quad \iota_\phi|_{\mrm{Alive}(\phi)} : \mrm{Alive}(\phi) \to \mrm{Alive}(\phi) \text{ (対合)}
`$

次のように略記します。

$`\quad \iota_{\phi, \mrm{Dead}} := \iota_\phi|_{\mrm{Dead}(\phi)}\\
\quad \iota_{\phi, \mrm{Alive}} := \iota_\phi|_{\mrm{Alive}(\phi)}
`$

$`\alpha`$ のペアリング対合 $`\iota`$ と、$`\phi`$ のペアリング対合 $`\iota_\phi`$ は無関係ではありません。ボディフラグに対しては一致します。

$`\quad \iota|_{\mrm{Body}(\alpha)} = \iota_\phi|_{\mrm{Body}(\alpha)}\;: \mrm{Body}(\alpha) \to \mrm{Body}(\alpha)`$

ボディフラグはペアとなって内部辺を形成しますが、$`\iota`$ による内部辺も $`\iota_\phi`$ による内部辺も同じです。$`\iota`$ と $`\iota_\phi`$ の差が出るのはテールフラグに対する作用の部分です。$`\iota_\phi`$ の亡骸テールフラグに対する作用には次の条件が付きます。

$`\iota_\phi|_{\mrm{DeadTail}(\phi)}`$ は不動点を持たない対合である。

$`\mrm{DeadTail}(\phi)`$ は次の意味です。

$`\quad \mrm{DeadTail}(\phi) := \mrm{Dead}(\phi) \cap \mrm{Tail}(\alpha)\\
\quad \mrm{AliveTail}(\phi) := \mrm{Alive}(\phi) \cap \mrm{Tail}(\alpha)\\
\quad \mrm{DeadBody}(\phi) := \mrm{Dead}(\phi) \cap \mrm{Body}(\alpha)\\
\quad \mrm{AliveBody}(\phi) := \mrm{Alive}(\phi) \cap \mrm{Body}(\alpha)
`$

$`\iota_\phi|_{\mrm{AliveTail}(\phi)}`$ には何の条件も付けません。不動点があってもかまいません。

まとめると：

$`\iota_\phi|_{ \mrm{DeadTail}(\phi) }`$ ：不動点なし対合、消去される縮減仮想辺を定義する。
$`\iota_\phi|_{ \mrm{AliveTail}(\phi) }`$ ：任意の対合（条件なし）、ターゲット側にコピーされる外部辺と架橋仮想辺を定義する。
$`\iota_\phi|_{ \mrm{DeadBody}(\phi) }`$ ： $`\iota`$ と一致、消去される縮減実辺を定義する。
$`\iota_\phi|_{ \mrm{AliveBody}(\phi) }`$ ： $`\iota`$ と一致、ターゲット側にコピーされる内部辺を定義する。

ここで、仮想辺とは、$`\alpha`$ の辺ではないが、$`\iota_\phi`$ によって新たに作り出された辺（フラグの同値類）のことです。仮想辺は、$`\alpha`$ のターゲットフラグのペアになります。架橋、縮減については「半グラフの二重圏と半グラフ変形」を参照してください。

境界写像 $`\bdry, \bdry'`$ については次の条件が付きます。

$`\require{AMScd}
\quad \begin{CD}
\mrm{Alive}(\phi) @>{\mrm{id}_{ \mrm{Alive}(\phi) }}>> \mrm{Alive}(\phi) \\
@V{\bdry|_{\mrm{Alive}(\phi)}}VV @VV{\bdry'|_{\mrm{Alive}(\phi)}}V \\
V @>{p_\phi}>> V'
\end{CD}\\
\quad \text{commutative in }{\bf Set}
`$

$`\quad \begin{CD}
\mrm{Dead}(\phi) @>{\iota_{\phi, \mrm{Dead}} }>> \mrm{Dead}(\phi) \\
@V{\bdry|_{\mrm{Dead}(\phi)}}VV @VV{\bdry'|_{\mrm{Dead}(\phi)}}V \\
V @>{p_\phi}>> V'
\end{CD}\\
\quad \text{commutative in }{\bf Set}
`$

上の二番目の可換図式の意味は、$`\mrm{Dead}(\phi)`$ 上では、実辺も仮想辺も $`V'`$ に対する自己ループ辺に移されることです。

以上の色々な条件は、ターゲット半グラフと各種写像を作るときに必要となります。まとめておくと：

$`\mrm{Dead}(\phi), \mrm{Alive}(\phi)`$ は、$`F = F(\alpha)`$ の直和分割で、それぞれが、$`\iota = \iota_\alpha`$ に対しても $`\iota_\phi`$ に対しても閉じている。
$`\iota_\phi`$ はボディフラグの集合 $`\mrm{Body}(\alpha) \subseteq F`$ 上では $`\iota`$ と一致する。
$`\iota_\phi`$ は、$`\mrm{DeadTail}(\phi)`$ 上で不動点を持たない。
$`\mrm{Alive}(\phi)`$ 上の境界写像の条件を満たす（上記の可換図式）。
$`\mrm{Dead}(\phi)`$ 上の境界写像の条件を満たす（上記の可換図式）。

DOA構造から作られる各種半グラフ

$`\phi/\alpha`$ を、半グラフ $`\alpha`$ 上のDOA構造とします。$`F(\alpha)`$ は次のように分類できます。

	生存フラグ	亡骸フラグ
テールフラグ	生存外部辺または架橋仮想辺を構成	縮減仮想辺を構成
ボディフラグ	生存内部辺を構成	縮減実辺を構成

$`F = F(\alpha)`$ と $`\iota_\phi`$ を組み合わせて商集合を作りましょう。

$`\quad E(\phi) := F/\iota_\phi`$

$`\mrm{Body}(\alpha)`$ 上では $`\iota = \iota_\phi`$ なので、$`E = E(\alpha)`$ の内部辺と $`E(\phi)`$ の内部辺は同じです。このことは次のように書けます。

$`\quad \mrm{Int}E(\alpha) = \mrm{Int}E(\phi)`$

フラグの集合 $`\mrm{DeadTail}(\phi)`$ を $`\iota_\phi`$（の同値関係）で割った商集合は、ゴースト辺〈ghost edge〉の集合と呼びます。ゴースト辺は縮減仮想辺と同じです。生存外部辺は、$`\iota_{\phi, \mrm{Alive}}`$ の不動点で作られる辺、架橋仮想辺は、$`\iota_{\phi, \mrm{Alive}}`$ の非不動点で作られる辺です。

[補足]
バーガー／カウフマンはゴースト辺を重視しており、もとの半グラフの内部辺をすべて外部辺に置き換えて（内部辺を切断して）、ゴースト辺だけを内部辺とした半グラフをゴースト半グラフと呼んでいます。ゴースト半グラフに、半グラフ変形の特性がエンコードされているのは確かですが、ゴースト半グラフで半グラフ変形が記述できるわけではありません。
[/補足]

上記のような仮想辺を持つ半グラフから、半グラフ変形の指令半グラフ〈instruction semi-graph〉を作るのは容易です。実辺（$`\alpha`$ の内部辺と生存外部辺）と仮想辺（架橋仮想辺と縮減仮想辺）に指令ニモニックを割り当てます。「半グラフの二重圏と半グラフ変形」では、「仮想辺の一部とならない外部辺には指令ニモニックは付きません。」と書きましたが、仮想辺の一部とならない外部辺〈生存外部辺〉にもNop指令ニモニックを割り当てることにします。

生存内部辺に $`\mrm{N}`$ を割り当てる。
生存外部辺に $`\mrm{N}`$ を割り当てる。
架橋外部辺に $`\mrm{B}`$ を割り当てる。
縮減仮想辺に $`\mrm{S}`$ を割り当てる。
縮減実辺に $`\mrm{S}`$ を割り当てる。

こうして作られた指令半グラフを $`\mrm{Instr}(\phi/\alpha)`$ とします。この指令半グラフには $`\mrm{C}`$〈切断指令ニモニック〉が無いことから、半グラフ架橋・縮減変形を記述していることが分かります。

次に、DOA構造 $`\phi/\alpha`$ の中間半グラフ〈intermediate semi-graph〉を定義します。中間半グラフは、ソース半グラフ $`\alpha`$ とターゲット半グラフ $`\beta`$ （後述）の中間的存在の半グラフです。$`\gamma`$ を中間半グラフだとして、記法を簡略にするために次のように書きます。

$`\quad \gamma = (V', F', \bdry', \iota')`$

$`V', \bdry'`$ は既に定義した集合・写像ですが、$`V', \bdry'`$ も含めて定義を書くと：

$`\quad V' := V/\!\sim_\phi\\
\quad F' := F\\
\quad \bdry' := \bdry \,; p_\phi \\
\quad \iota' := \iota_\phi
`$

$`\mrm{id}_F : F \to F'`$ を、中間半グラフへのフラグ写像〈flag map〉（実体は恒等写像）、$`p_\phi : V \to V'`$ を中間半グラフへの頂点写像〈vertex map〉といいます。頂点写像とフラグ写像の組 $`(p_\phi, \mrm{id}_F)`$ は半グラフ射（二重圏 $`{\bf SemiGraphDC}`$ の縦1-射）になるとは限りません。が、グラフ変形を記述する写像だとは言えます。

DOA構造の条件から、次が言えます。

中間半グラフのフラグの集合は、$`\alpha`$ のフラグの集合である。
中間半グラフの内部辺は、$`\alpha`$ の生存内部辺、架橋仮想辺、実縮減辺、ゴースト辺〈縮減仮想辺〉からなる。
中間半グラフの外部辺は、$`\alpha`$ の生存外部辺からなる。
中間半グラフの内部辺のうち、実縮減辺、ゴースト辺〈縮減仮想辺〉は自己ループ辺になっている。その他にも自己ループ辺はあるかも知れない（生存内部辺として）。

最後に、DOA構造 $`\phi/\alpha`$ のターゲット半グラフ〈target semi-graph〉を定義します。$`\beta`$ をターゲット半グラフだとして、記法を簡略にするために次のように書きます。

$`\quad \beta = (V'', F'', \bdry'', \iota'')`$

定義は次のようです。

$`\quad V'' := V' = V/\!\sim_\phi \\
\quad F'' := \mrm{Alive}(\phi)\\
\quad \bdry'' := \bdry'|_{\mrm{Alive}(\phi)}\\
\quad \iota'' := \iota'|_{\mrm{Alive}(\phi)}
`$

中間半グラフからターゲット半グラフの構成は非常に簡単で、$`\mrm{Dead}(\phi)`$ を捨ててしまうだけです。ターゲット半グラフでは、$`\mrm{Alive}(\phi)`$ だけが生き残り、$`\mrm{Dead}(\phi)`$ は消滅しています。消滅したフラグは、指令グラフで $`\mrm{S}`$（縮減）指令でマークされていた辺／仮想辺を構成するフラグ達です。

この節で定義した半グラフを次のように書きます。

DOA構造 $`\phi/\alpha`$ の指令半グラフ： $`\mrm{Instr}(\phi)`$
DOA構造 $`\phi/\alpha`$ の中間半グラフ： $`\mrm{Med}(\phi)`$
DOA構造 $`\phi/\alpha`$ のターゲット半グラフ： $`\mrm{Trg}(\phi)`$

頂点同一視関係と頂点マージ変形

「半グラフの二重圏と半グラフ変形」において、指令半グラフがあれば、それで半グラフ変形を記述できるような書き方をしてしまったのですが、指令半グラフでは記述できない頂点同一視があります。

頂点同一視〈vertex identification〉とは、DOA構造の一部である同値関係 $`\sim_\phi`$ または、同値関係から誘導される写像 $`p_\phi`$ のことです。指令半グラフの情報からも次の頂点同一視は分かります。

実縮減辺の両端の頂点は同一視される。
仮想縮減辺の両端の頂点は同一視される。

しかし、それ以外の頂点同一視があってもかまいません。例えば、すべての頂点を一点にしてしまう頂点同一視も許します。以下の図はその例です。

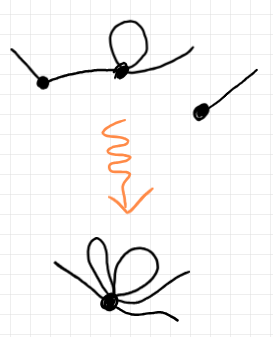
3つの頂点を1点に潰していますが、内部辺と外部辺はそのまま残っています。すべての内部辺が（もとがループでなくても）自己ループ辺になります。外部辺は何も変わりません。

この例にように、頂点が同一視されるが辺（内部辺／外部辺）がそのまま残る半グラフ変形は頂点マージ変形〈merger〉と呼びます。merger はボリソフ／マニンの用語です。

もうひとつ典型的な頂点マージ変形として、頂点同一視関係 $`v \sim_\phi w`$ を次のように定義します。

$`v, w\in V(\alpha)`$ に対して、$`v`$ と $`w`$ を結ぶ $`\alpha`$ のパスが存在する。

これは、半グラフの連結成分を定義する同値関係と同じです。この同値関係と、次の構成素でDOA構造を定義します。

$`\quad \mrm{Alive}(\phi) := F(\alpha)\\
\quad \mrm{Dead}(\phi) := \emptyset\\
\quad \iota_\phi := \iota_\alpha
`$

すると、連結成分ごとに頂点をマージして、辺はそのまま残す頂点マージ変形が定義できます。この頂点マージ変形の後で、すべての内部辺を（縮減で）消去すると、コステロが利用した標準的半グラフ変形が得られます。

DOA構造と半グラフ変形

半グラフ射（半グラフ変形ではない）で可逆なものを半グラフのアルファ変換〈alpha conversion〉と呼びました（「コステロの半グラフ圏から二重関手意味論へ」参照）。半グラフ $`\beta`$ と $`\gamma`$ のあいだのアルファ変換は次のように書くとします。

$`\quad \beta \overset{\to}{\sim} \gamma \In {\bf SemiGraphG}`$

半グラフ $`\alpha`$ 上のDOA構造 $`\phi = \phi/\alpha`$ と、$`\beta = \mrm{Trg}(\phi)`$ からのアルファ変換

$`\quad f: \beta \overset{\to}{\sim} \beta' \In{\bf SetmiGraphG}`$

の組 $`(\phi/\alpha, f)`$ は、$`\alpha`$ をソース〈域〉、 $`\beta'`$ をターゲット〈余域〉とする半グラフ変形を表現できます。なんなら、組 $`(\phi/\alpha, f)`$ を半グラフ変形の定義に採用してもかまいません。

半グラフ $`\alpha`$ 上のすべてのDOA構造の集合を $`\mrm{DOA}(\alpha)`$ とします。$`\alpha`$ を固定したとき、DOA構造の構成素である $`\mrm{Alive}(\phi), \mrm{Dead}(\phi), \iota_\phi, \sim_\phi`$ の候補はどれも有限個しかありません。$`\alpha`$ が有限的組み合わせ構造だからです。有限個の候補を組み合わせたDOA構造も有限個しかありません。したがって、$`\mrm{DOA}(\phi)`$ は有限集合です。

半グラフのアルファ変換の差を無視すれば、$`\alpha`$ をソース〈域〉とする半グラフ変形は有限個しかないことになります。半グラフを対象として、半グラフ変形を射とする圏（半グラフ二重圏の水平圏）は、本質的に小さい〈essentially small〉圏です。対象の同型類は可算無限個しかなく、ホムセットは有限集合です。

つまり、半グラフと半グラフ変形の圏は、有限的・具体的に調べ上げることが（原理的には）可能です。DOA構造 $`\phi/\alpha`$ が調べ上げるべきデータとなります。