なぜ引き算なしでも大丈夫なのか

引き算はなくてもだいたい大丈夫で提示した問題。MarriageTheoremさんやささはらさんに回答していただきました。

僕は、なんか持って回った証明しか思いつかなかったんですが、短くて簡略な方法で示せるのかも知れません。興味と時間がある方は考えてみてください。

と書いたように、僕が思いついた方法は直接的ではないので不満が残りますが、幾何学的に明確なイメージを持てることはメリットかもしれないので、書いておきます。

内容：

1. 不定方程式の非負整数解とは
2. 解が1つあるなら、もう1つ解がある
3. 解が2つあるなら、無限に解がある
4. 直線をズリズリとずらしてみる
5. 一般化するには

●不定方程式の非負整数解とは

a, b, cは整数だとして、方程式（整数の不定方程式）ax + by = c を考えます。ユークリッドの互除法とかイデアル論とかを使えば次の結果を示せます。

• aとbの最大公約数をgとして、cがgの倍数のとき、そのときに限り ax + by = c が解ける（整数の範囲内でx, yが見つかる）。

例えば、4x + 6y = c は、cが偶数なら解けます。特に、aとbが互いに素（g = 1）のときは、

• 任意のcに対して ax + by = c が解ける。

ことになります。例えば、2x + 3y = c は、cが何であっても解けます。MarriageTheoremさんが指摘なさっていたように、aとbが互いに素のときを考えれば十分です。以下、aとbは互いに素だと仮定します。具体例としては、a = 2, b = 3 を使うことにしましょう。

さて、件の問題は、「a > 0、b > 0、aとbは互いに素の状況で、cがある程度大きければ（とあるNに対してc≧N）、ax + by = c が非負整数の範囲で解ける」ことを示す問題でした。

●解が1つあるなら、もう1つ解がある

まず、cを固定して考えます。たとえば、c = -2 とします。2x + 3y = -2 が解けることは上記の結果から保証されています。実際、x = 2, y = -2 とすると、2・2 + 3・(-2) = -2 です。(x, y) = (2, -2) は解ですね。解は1つだけでしょうか？ 実は、1つ解があると別な解を構成できます。

(x, y) = (n, m) が解だとして、n' = n - b, m' = m + a とすると、(x, y) = (n', m') も解です。それは次の計算でわかります。

   an' + bm'

 = a(n - b) + b(m + a)

 = an - ab + bm + ba

 = an + bm

 = c （an + bm = c だったので）
つまり、an' + bm' = c

2x + 3y = -2 の例だと、(x, y) = (2, -2) だけでなく (x, y) = (-1, 0) も解だとわかります（下図）。

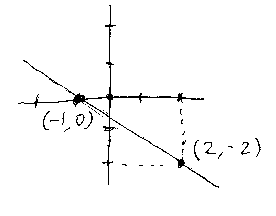
●解が2つあるなら、無限に解がある

(n, m)と(n', m')が ax + by = c の解のとき、ベクトル記法で、

• (n, m) + t[(n', m') - (n, m)] （tは任意の整数）

も解となります。2x + 3y = -2 の例だと、

• (2, -2) + t[(-1, 0) - (2, -2)] = (2, -2) + t(-3, 2)

も解を与えます。

図形的に言えば、点(2, -2)を基点として方向ベクトル(-3, 2)で与えられる直線上の、等間隔に並ぶ点達がすべて解になるということです。

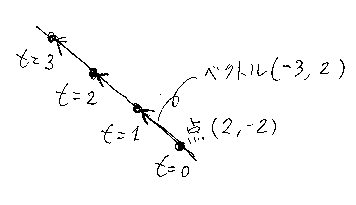
一般的な状況での計算を、ベクトルを太字で表し、内積を「・」として実行すると、次のようになります。

 a = (a1, a2) = (a, b),

 n = (n1, n2) = (n, m),

 n' = (n1', n2') = (n', m') とする.

 a・n = c, a・n' = c が成立しているとして；

 

   a・(n + t(n' - n))

 = a・n + t(a・n' - a・n))

 = c + t(c - c)

 = c

●直線をズリズリとずらしてみる

2x + 3y = -2 の例だと、まず点(2, -2)と点(-1, 0)が解だとわかり、他にもたくさん解があることもわかりました。それらの解は (2, -2) + t(-3, 2) （t = ..., -2, -1, 0, 1, 2, ...）の形に書けます。解である点の間隔は sqrt[(-3)² + 2²] = sqrt(13) ≒ 3.6 です。点の間隔を計算するときに、ax + by = c のcは使ってなくて、cによらずに sqrt[(-b)² + a²] = sqrt(a² + b²) 間隔で並んだ点達が解となることがわかります。

ax + by = c は平面図形としては直線となりますが、cを動かしてやると、aとbで決まる定まった傾きのまま、平行にズリズリとずれます。例えば、2x + 3y = c に対して、cの値を変えて何本か直線を描くと次のような感じです。

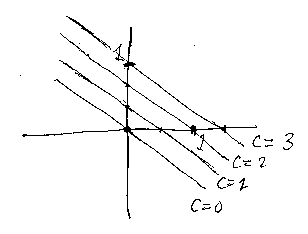
cの値をうまく取れば、直線 ax + by = c が第1象限を横切るようにできます。それだけでなく、第1象限により切り取られる線分の長さをいくらでも長くすることができます（下図）。

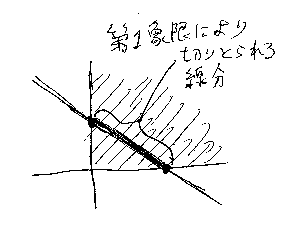
a > 0, b > 0 の状況（上の絵はそうなっている）だと、cを増やしていくと、第1象限により切り取られる線分の長さも順調に増えます。この線分の長さが増えれば、ax + by = c の整数解である点（直線上に等間隔で並んでいる）が、いずれ必ず線分上に現れます。現れたその点は第1象限にあるので、もとの不定方程式 ax + by = c の非負整数解を与えます。

つまり、cがある程度大きくなると、ax + by = c の非負整数解（x ≧ 0, y ≧ 0）が必ず存在する（存在せずにはおられない）ことになります。

●一般化するには

a₁x₁ + ... + a_kx_k = c のときも同じ方法が使えます。不定方程式の解達は、k次元ユークリッド空間の超平面（アフィン部分空間）内に、格子点のように配置されます。係数a₁, ..., a_kが全部正なら第1象限（正錐）と超平面の共通部分は単体（三角形の一般化）になり、cを増やすと単体の体積もどんどん増えます。体積が十分大きな凸体は格子点を含む*1ので、不定方程式は非負整数解を持ちます。

*1:[追記]ここは、もっとチャントした記述と議論が必要です。[/追記]