1 と 1.0 が等しいかどうか？グロタンディーク構成で考えてみる

最近、「1 と 1.0 は等しいか？」という問題を考えました（ホント）。インデックス付き圏のグロタンディーク構成に基づいて考えて、答を出しました（作り話）。実話かどうかはともかくとして、「1 と 1.0 は等しいか？」をグロタンディーク構成を使って解く話をします。

僕は、「圏の例はそこらじゅうにいくらでも転がっている」ということを割と強調するのですけど、これも「そこらじゅうにいくらでも転がって」いた事例ですね。

関連するエントリー：

内容：

集合を圏とみなす話
インデックス付き集合はインデックス付き圏である
整数と実数のインデックス付き圏
グロタンディーク構成
直和とその上の関係
で結局、1 と 1.0 は等しいの？

集合を圏とみなす話

圏は、対象と射から構成されます。対象だけでは圏になりません。最低でも、対象と一対一に対応する恒等射は必要です。対象と恒等射だけあればそれで圏となります。

集合Sが与えられたとき、Sを対象の集合とする最小の圏Cは次のようにして作れます。

|C| = Obj(C) = S
x = y ならば C(x, y) = C(x, x) = {id_x}
x ≠ y ならば C(x, y) = 空集合

このようにして作った圏は離散圏（discrete category）と呼ばれます（「はじめての圏論その第3歩：極端な圏達」参照）。集合と離散圏は事実上同じものです。単なる集合を圏とみなしたいときは、対応する離散圏を作ってやればいいのです。

離散圏では、次が成立することに注意しましょう。

xとｙが等しい ⇔ xからyへの射が存在する
xとｙが異なる ⇔ xからyへの射は存在しない

離散圏においては、次が言えるのです。

射（の存在）が、対象の等しさの定義を与える。

これはとても大事なことです。テストに出ます（ウソッ、テストないし）。

集合のあいだの任意の写像Fは関手とみなせます。これは、次の意味で、写像が等しさを保つからです。

x = y ならば F(x) = F(y)

等しさとは射のことだったので、言い換えると：

f:x→y ならば F(f):F(x)→F(y)

これはまさに関手の定義ですね。

インデックス付き集合はインデックス付き圏である

インデックス付き圏とは、Iをベース圏（インデックスの圏）として、I→Cat という反変関手のことでした。ここで、Catは「圏の圏」です。上で述べた「集合を圏とみなす操作」により、Set⊆Catと考えてよいことになります。であるなら、I→Set という反変関手もインデックス付き圏となります。

特に、Iが離散圏のときは、集合Iをインデックスの集合とする集合族になります。Iが離散圏＝集合のときは、反変関手と共変関手の区別はなくなります。任意の関手 S:I→Set は、(S_i)_i∈I という形で書け、インデックス付き圏とみなせます。

Iが順序集合のとき、Iでインデックス付けられた集合の増加族（または減少族）は、I→Set という関手になるので、インデックス付き圏の例となります。集合の増加族とは、「i ≦ j ならば S_i ⊆ S_j」となるような集合族です。≦ と ⊆ を射と解釈すれば、集合の増加族や減少族を関手とみなせます。

Iが離散とは限らない一般の圏のとき、a∈|I| を固定して、反変ホムセット関手 hom^a = Hom_I(-, a) = I(-, a) を考えましょう。hom^a:I→Set は反変関手となるので、インデックス付き圏の例です。Iが順序集合のときは、hom^aは、xに「x ≦ a であるか？」の真偽値を対応させる関手です。ただし、真を単元集合、偽を空集合と解釈します。

「I→Set という関手をインデックス付き圏とみなして何がうれしいの？」と聞かれると、「たいしてうれしくない」と答えることになるでしょう(苦笑)が、次の点では少しうれしいです。

Set値関手をインデックス付き圏とみなせば、グロタンディーク構成で平坦化した圏を作れる。
平坦化した圏を使ってファイブレーションを定義できる。
ファイバー圏の例をたくさん作れる。

この方法で作ったファイバー圏がいつでも面白いとは限りません（つまらない例もある）が、ともかく事例の大量生産が可能となります。

整数と実数のインデックス付き圏

さて、本題である「1 と 1.0 は等しいか？」を考えるための舞台となるインデックス付き圏を作りましょう。

ベース圏Iは次のような圏です。

Iの対象は {r, i} である。'r'と'i'は単なる記号と考える。
恒等射以外の射は、j:r→i だけである。
結合は自明。

Obj(I) = |I| = {r, i}, Mor(I) = {id_r, id_i, j} なので、Iは、対象が2個、射が3本の有限圏です。

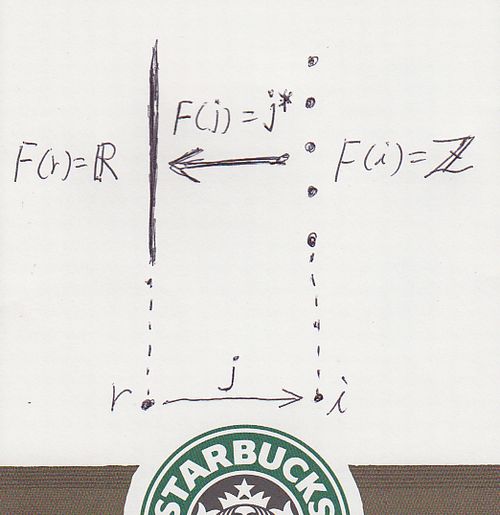
反変関手 F:I→Set を次のように定義します。

F(r) = R = 実数の集合
F(i) = Z = 整数の集合
F(j) = (Z ⊆ R という包含写像)

絵を描けば次のような感じ（スターバックスのロゴは気にしないでください）。

グロタンディーク構成

今定義したインデックス付き圏 F:I→Set に対してグロタンディーク構成をします。必要なら、「インデックス付き圏のグロタンディーク構成」を復習してください。以下では、グロタンディーク構成でFを平坦化した圏をCとします。

圏Cの対象を調べましょう。x∈R（xは実数）、n∈Z（nは整数）として、圏Cの対象は (r, x) または (i, n) の形をしています。具体例を出せば、(r, 3.14) とか (i, 5) とか。記号'r'は実数であることの目印で、記号'i'は整数であることの目印です。つまり、ペアの第1成分がタイプタグになっているわけです。Catyのtagged-value記法を使えば、@r 3.14、 @i 5 と書けます。要するに、圏Cの対象は、明示的にタイプタグが付いた実数または整数なんです。

次に圏Cの射を調べましょう。グロタンディーク構成（平坦化）の定義をちゃんと確認してくださいね（「インデックス付き圏のグロタンディーク構成」）。ベース圏（インデックスの圏）の射で、恒等は自明なので*1、j:r→i だけを考えれば十分です。

非自明なCの射は、(j, f):(r, x)→(i, n) という形をしています。グロタンディーク構成の定義から、fは j^*(n) から x への射です（j^* は F(j) の略記）。ところが、F(r) = R は離散圏なので、「j^*(n) から x への射」は恒等射しかありません。つまり、「j^*(n) から x への射」が存在するなら、「j^*(n) = x」です。

j^* = F(j) は、Z→R という包含写像でした。j^*(n) は、「実数とみなされた整数n」のことです。例えば、j^*(1)は「実数とみなされた整数1」です。「実数とみなされた整数1」を 1.0 と表記することにします。j^*(1) = 1.0、j^*(2) = 2.0、j^*(0) = 0.0、j^*(-1) = -1.0 などと書きます。

「j^*(n) から x への射」に話を戻して、射の存在は「j^*(n) = x」を意味するのでした。これは、「xは、実数とみなされたnである」ことを意味します。「xは、実数とみなされたnである」ことと、(r, x)→(i, n) という射の存在は同値です。

特に：

(r, x)→(i, 1) という射の存在は、x = 1.0 と同値

あるいは、

(r, 1.0) と (i, 1) のあいだには射が存在する。これ以外に (r, x)→(i, 1) という射は存在しない。

どうでしょう。平坦化した圏Cの形が見えてきましたか？絵にまとめておきましょう。

1本の連続直線（実数）とパラパラの点の集まり（整数）があり、連続直線上の格子点から、対応する整数点に向けて矢印が出ている形になります。先走りして（まだ説明してない）ファイブレーション射影も描くと、連続直線の影が'r'に、パラパラ点達の影が'i'に落ちて、ハシゴの横木のような矢印達の影が'j'に落ちます。

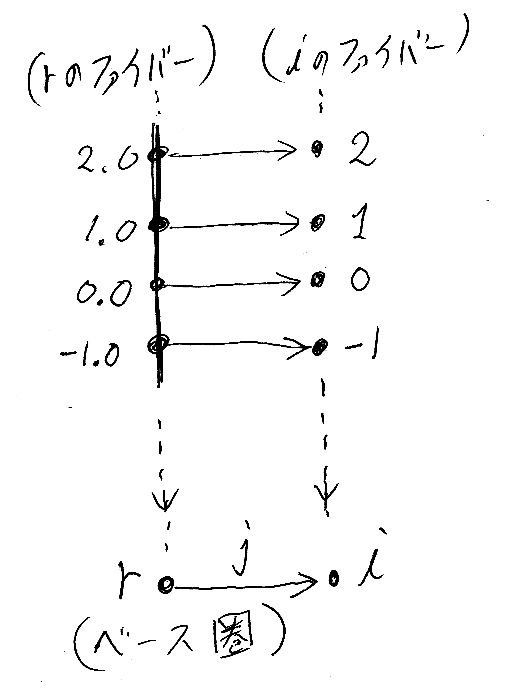
この例では、ベース圏の非自明な射はjしかありません。ベース射jと、ベース対象i上のファイバー内の対象（すなわち整数）を取ったとき、対応する横木がデカルト射になっています。整数値の引き戻し対象（pullback object）は対応する実数値、例えば整数値1に対する実数値1.0です。このファイバー圏では、射はみんなデカルト射で、垂直射（ファイバー内に収まる射）は恒等射です。

次の節では、今行ったグロタンディーク構成を、もっと慣れ親しんだ概念や手法を使って見直してみます。

直和とその上の関係

我々の問題は「1 と 1.0 は等しいか？」でした。この設問を少しゆるい形にして「1 と 1.0 は何の関係もない別物か、それとも何らかの関係があるのか？」としましょう。別な言い方をすると、「整数の集合Zと実数の集合Rを合わせた集合はどんな形をしているのか？」という設問です。もちろん、「合わせた集合」とか「どんな形」が曖昧な表現なので、これをより正確にする必要があります。

通常の数学では、Z⊆R と考えます。しかし、コンピュータでは整数と実数（浮動小数点数）のバイナリフォーマットも演算アルゴリズムもまったく違うので、Z∩R = 空集合と考えた方が実情に近いでしょう。一般的に、2つの集合に包含関係があるのか、共通部分があるのか、まったく離れている（disjointである）のか、などは難しい問題です。人為的な定義を天下りに与えられるならいいのですが、現象のモデルとして登場した集合のときは、よくワカンナイ場合も多いでしょう。

今回のZとRのケースも、計算の文脈ではよくワカンナイ状況です。こんなときはまず、ZとRをとりあえず別物と考えて直和を作ってみます。直和を作る標準的な方法は弁別子を添える方法ですが、弁別子はタイプタグと同じものです。弁別子＝タイプタグを、実数にはr、整数にはiと割り当てると、直和の定義は次のとおり。

R + Z = {r}×R ∪ {i}×Z

もうお分かりですね。この直和は、グロタンディーク構成でFを平坦化した圏Cの「対象の集合」と同じです。

Z→R という包含写像を図示すると、整数から実数に向かう矢印を描くことになります。グロタンディーク構成では逆に、実数から整数に向かう矢印が描かれます。どっちでも通用するように矢印の方向を省略すると、次の図のような、連続直線から横向きの枝が何本も出た図形になります。

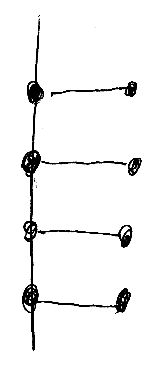
実数xと整数nが図の横木でつながっているなら、x 〜 n と記すことにします。「〜」は、R×Zの部分集合に対応するので、RとZのあいだの二項関係です。関係「〜」を実数どうし、整数どうしの場合にも拡張しましょう。

x, y∈R のとき x 〜 y とは x = y のこと
n, m∈Z のとき n 〜 m とは n = m のこと

これで、「〜」は、集合 R + Z 上の二項関係になりました。この関係は同値関係ではありませんが、順序関係になっています（記号が順序っぽくないですが）。つまり、次が成立します。

α 〜 α
α 〜 β、β〜γ ならば α〜γ
α 〜 β、β〜α ならば α = β

「〜」は、集合 R + Z に順序構造を定義します。順序集合は圏とみなせます（「はじめての圏論その第3歩：極端な圏達」参照）。こうして構成された圏は、グロタンディーク構成で構成された圏を再現します。

で結局、1 と 1.0 は等しいの？

前節で導入した関係「〜」では、 1.0 〜 1.0、 1 〜 1、 1.0 〜 1 は言えます。しかし、対称性を持たないので、1 〜 1.0 は言えません。確実に言えるのは、「1 と 1.0 はある関係で結ばれている」ことです。圏論の言葉で言えば、「1 と 1.0 を繋ぐ射がある」となります。これからたただちに「1 と 1.0 は等しい」とは言えませんが、「用途によっては等しいとみなしてよい」くらいは言えます。

関係「〜」を対称化すると同値関係になるので、商集合を作ることができます。この場合は、整数の集合Zを実数の集合Rに吸収することになり、商集合は（整数を内部に吸収した）実数集合です。

圏論的な考え方・やり方では、無理に対称化したり商集合を作ったりはしません。非対称な関係「〜」、あるいは（同じことですが）平坦化した圏をそのままの形にしておき、必要に応じて「〜」を等号のごとく扱います。「ほんとに同じじゃないけど、まー等しいと言ってもいいんじぇね」てな態度です。この態度を精密に記述するためには、比較セル（comparison cell/morphism）を使います。比較セルは、ゆるい等号を与えます。

「〜」は、ゆるい等号、つまり比較セルの初歩的な例です。1.0 〜 1 は成立しているので、「1 と 1.0 は、ほんとに同じじゃないけど、まー等しいと言ってもいいんじぇね」が答です。

*1:「自明」と書いてあったら用心が必要です。自分で確認しましょう。