豊饒圏（ピノキオ）が圏（人間）になる物語 - 檜山正幸のキマイラ飼育記 (はてなBlog)

ジョン・バエズ（John C. Baez）がどこかで、「豊饒圏はピノキオのようなものだ」と言ってました。ピノキオは人間ではないがまるで人間のように振る舞う -- 豊饒圏は圏ではないがまるで圏のように振る舞う。ピノキオは物語の最後にほんとうの人間になれる -- 豊饒圏もやはりほんとうの圏になれる。と、そんな話。

[*1]

内容：

ピノキオ
ピノキオの動き方
人間になりたい
人間になれた！

ピノキオ

Vを豊饒化のベース圏（enriching category）とします。Vはモノイド圏 V = (V, $\otimes$ , I) である必要があります。ここではVがデカルトモノイド圏だとします。つまり、Vのモノイド積 $\otimes$ はデカルト積（＝直積）になっているとします*2。

Xを集合（大きな集合＝類でもよい）として、Xを対象類としてVで豊饒化された圏（V-enriched category）をPとします。Pはほんとうの圏ではないのでイタリック体文字にはしないことにします。文字Pを使ったのはピノキオを意識してです。Pは次のモノから構成されます。

hom_P:X×X→|V| という写像
(a, b, c)∈X×X×X で添字付けられたVの射の族 γ_a,b,c:hom_P(a, b) $\otimes$ hom_P(b, c)→hom_P(a, c)
a∈X で添字付けられたVの射の族 ι_a:I→hom_P(a, a)

これらは、豊饒圏としての結合律と左右の単位律を満たすとします（詳細は次節）。hom_PはV値のホム対象ですが、hom_P:X×X→|V| を単に P:X×X→|V| と書いて、さらに記号の乱用で P = (P, γ, ι) と書きます。

ピノキオの動き方

ピノキオは人間と同じように動きます。しかしピノキオは生身の人間ではなくて木の人形なので、その動き方はどこか人間とは違います。ピノキオ（豊饒圏）の動き方を正確に記述するには、けっこう細かい分析が必要です。

P = (P, γ, ι) がV-豊饒圏のとき、PはおおよそV内のモノイドのように考えることができます。なので、モノイドの定義を復習しておきましょう。

MがVの対象だとして、μ:M $\otimes$ M→M、η:I→M をVの射として、(M, μ, η)がモノイドだとは、次の法則を満たすことです。上から順に、結合律、左単位律、右単位律です。id_Mを単にMと書いています。

(μ $\otimes$ M);μ = (M $\otimes$ μ);μ : M $\otimes$ M $\otimes$ M→M
(η $\otimes$ M);μ = M : M→M
(M $\otimes$ η);μ = M : M→M

実はこれは少し不正確で、モノイド圏の結合性・構造同型射 α_M,M,M: (M $\otimes$ M) $\otimes$ M→M $\otimes$ (M $\otimes$ M) と単位性・構造同型射 λ_M:I $\otimes$ M→M、ρ_M:M $\otimes$ I→M （の逆射）を使ってチャンと書くと：

α_M,M,M^-1;(μ $\otimes$ M);μ = (M $\otimes$ μ);μ : M $\otimes$ (M $\otimes$ M)→M
λ_M^-1;(η $\otimes$ M);μ = M : M→M
ρ_M^-1;(M $\otimes$ η);μ = M : M→M

まー、この正確性はあんまり気にしなくてもいいと思いますが。

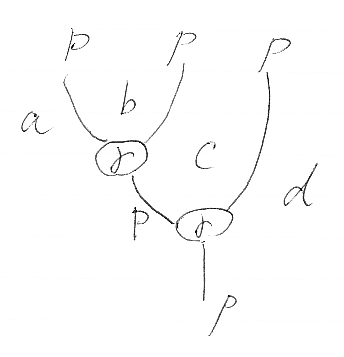
さて、P = (P, γ, ι) の結合律・左単位律・右単位律ですが、それはモノイドの法則に添字を付けた形をしています。まずは結合律：

(γ_a,b,c $\otimes$ P(c, d));γ_a,c,d = (P(a, b) $\otimes$ γ_b,c,d);γ_a,b,d : P(a, b) $\otimes$ P(b, c) $\otimes$ P(c, d)→P(a, d)

次のような絵（これは結合律の左辺）を見ながら書き下すといいでしょう。いつものストリング図です。

添字を省略してしまうと、

(γ $\otimes$ P);γ = (P $\otimes$ γ);γ : P $\otimes$ P $\otimes$ P→P

なので、モノイドの結合律と同じです。

左単位律、右単位律も同様です。構造同型射α^-1、λ^-1、ρ^-1まで入れた正確な形を、結合律も含めて書き下せば：

α_{P(a, b),P(b, c),P(c, d)}^-1;(γ_a,b,c $\otimes$ P(c, d));γ_a,c,d =(P(a, b) $\otimes$ γ_b,c,d;γ_a,b,d : P(a, b) $\otimes$ (P(b, c) $\otimes$ P(c, d))→P(a, d)
λ_{P(a, b)}^-1;(ι_a $\otimes$ P(a, b));γ_a,a,b = P(a, b) : P(a, b)→P(a, b)
ρ_{P(a, b)}^-1;(P(a, b) $\otimes$ ι_b);γ_a,b,b = P(a, b) : P(a, b)→P(a, b)

いちおうチャンと書きましたが、先頭に付いてるα^-1、λ^-1、ρ^-1は無視してもいいです*3。

人間になりたい

デカルトモノイド圏Vで豊饒化された圏 P = (P, γ, ι) に対して、通常の圏Cを定義します。Cの対象類とホムセットを次のように定義します。

|C| = X
C(a, b) = V(I, P(a, b))

圏C（今はまだ圏だと分かってませんが）の対象類はPの対象類と同じです。CのホムセットはVのホムセットを使って定義します。Vのホムセットは集合なので、a, b∈X に対するC(a, b)も集合になります。

Cの結合を与える写像を comp_a,b,c:C(a, b)×C(b, c)→C(a, c)、恒等射を id_a∈C(a, a) とします。compとidを定義するには次の事実に注意する必要があります。

V(C, A)×V(C, B) $\stackrel{\sim}{=}$ V(C, A $\otimes$ B)

これは、 $\otimes$ がVの直積であることから分かります。f:C→A, g:C→B in V として、デカルトペアリング <f, g> を作ると、それは V(C, A $\otimes$ B) に入り、上記の同型を与えます。この同型を φ_C,A,B と書くことにします。

さて、comp_a,b,c:C(a, b)×C(b, c)→C(a, c) の定義は次のような順番で作ります。

定義より、 C(a, b)×C(b, c) = V(I, P(a, b))×C(I, P(b, c))
φ_{I,P(a, b),P(b, c)}:V(I, P(a, b))×C(I, P(b, c))→V(I, P(a, b) $\otimes$ P(b, c)) は同型
γ_a,b,c:P(a, b) $\otimes$ P(b, c)→P(a, c) in V を後結合（post-compose）する写像を使って、 V(I, P(a, b) $\otimes$ P(b, c))→V(I, P(a, c)) を定義
定義より、V(I, P(a, c)) = C(a, b)

  C(a, b)×C(b, c)
 --------------------------------- 1. 定義より
  V(I, P(a, b))×V(I, P(b, c))
 --------------------------------- 2. φ_{I,P(a, b),P(b, c)}
  V(I, P(a, b)P(b, c))
 --------------------------------- 3. γ_a,b,c を後結合
  V(I, P(a, c))
 --------------------------------- 4. 定義より
  C(a, b)

id_aは、ι_a∈V(I, P(a, a)) のことだとします。

人間になれた！

前節の手順により、|C|, C(a, b), comp_a,b,c, id_a を作れます。あとは、compの結合律とidに関する左単位律／右単位律が成立していれば、Cは間違いなく圏になります。

前節の結合の定義を、f∈C(a, b) と g∈C(b, c) に関して具体的に書いてみましょう。f∈C(a, b) ⇔ f:I→P(a, b) in V、g∈C(b, c) ⇔ g:I→P(b, c) in V であることを思い出して下さい。

f;g = δ;(f $\otimes$ g);γ_a,b,c

ここで、δは単位対象Iの対角射 δ = Δ_I:I→I $\otimes$ I です。デカルト圏では、どんな対象Aについても、(A, Δ_A:A→A $\otimes$ A, !_A:A→I) がコモノイドになるので、(I, δ, id_I) はV内のコモノイドになります。δが余結合律を満たすことが重要です。

豊饒化ベース圏Vがデカルト圏だと仮定すると議論がし易いので、発見的な考察や手短な説明には好都合です。しかし、(I, δ, id_I) がコモノイドになることだけが重要で、Vがデカルト圏であることは必須ではありません。

デカルト圏でなくても、δ = λ_I^-1 と定義するとうまくいきます。しかし、δ = λ_I^-1 = ρ_I^-1 の証明はけっこう難しいようで、(I, δ, id_I) がコモノイドになることは一般的には自明ではありません。

上記の等式が f;g の定義を与えると思ってかまいません。こうして定義した結合（合成）「;」の結合律を示しましょう。テキスト等式では辛いので絵算を使います。(f;g);h を、先の定義を使って書くと；

δ;((δ;(f $\otimes$ g);γ_a,b,c) $\otimes$ h);γ_a,c,d

これを絵に描いて変形していきます。下の絵で、ラベルが付いてないワイヤーは単位対象Iを表し、Pとγの添字は省略しています。目線の移動などに関しては「絵算の威力をお見せしよう」にも例があります。

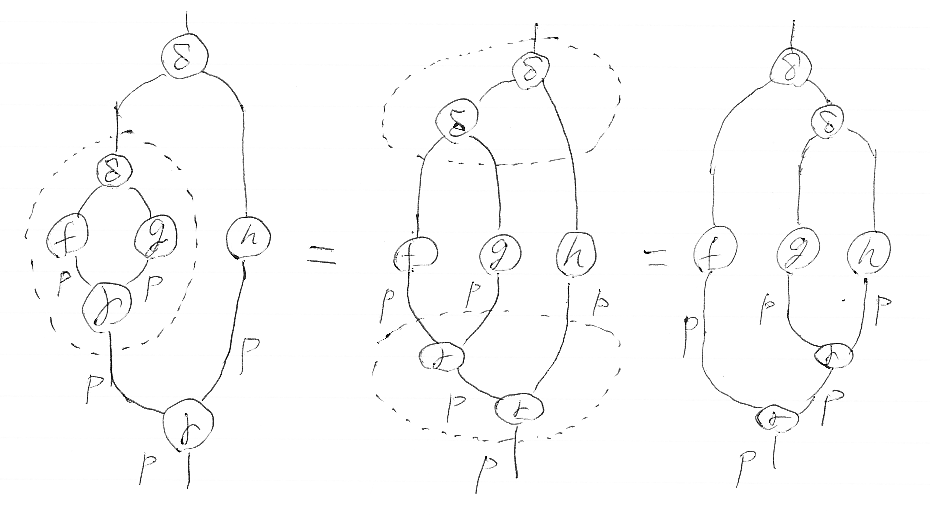
左側と真ん中の絵は同じですが、注目点を変えています。左側の点線枠は f;g を囲っています。真ん中では「上部の2つのδ」と「下部の2つのγ」に注目するように点線枠を付けています。「上部の2つのδ」に余結合律、「下部の2つのγ」に結合律を適用すると、右側の絵になります。右側のg, h付近に注目すると、これは g;h であることが分かり、右側の絵全体で f;(g;h) を表しています。

左単位律と右単位律も、絵算ではお決まりの変形と目線移動（注目点の変更）で示せます。

Pから作ったCは通常の圏です。CがピノキオPが人間になった姿です。「ピノキオの人間化＝豊饒圏から通常の圏の構成」は、ラムダ計算のラムダ抽象（関数項）や線形代数の行列（共変-反変の2階テンソル）が、圏の射を表すとみなしてよい根拠を与えます。

ラムダ計算や線形代数の場合は事情が特殊で、ピノキオ（＝豊饒圏）は最初から人形なのではなくて、もともとは人間だったのが魔法で人形に変えられたのです。その魔法の名は自己豊饒化です。デカルト閉圏やコンパクト閉圏では、自分自身を豊饒化ベース圏としての豊饒化が可能で、豊饒化しても元の圏の情報がそのまま保たれます。よって、今回説明した「脱豊饒化＝ピノキオの人間化＝豊饒圏から通常の圏の構成」により元の圏を再現できます。

豊饒化ベース圏Vの取り方により、豊饒圏から通常の圏を構成してもほとんど意味がないことがあります。例えば、豊饒圏とみなした一般化距離空間から圏を構成しても面白くありません。人形から人間になれても、どうでもいい人間になってしまってガッカリ、これなら人形のままのほうが良かった、みたいな。

ピノキオの人間化がどんな結果をもたらすかは様々ですが、ピノキオ（＝豊饒圏）を見たら、コイツを人間（通常の圏）にしたら何になる？と考えてみるのは面白いかも。

*1:画像は http://www.amazon.co.jp/dp/B005MATMMK より

*2:話を簡単にするためにデカルト性を仮定します。この仮定が絶対に必要なわけではありません。

*3:Vが厳密モノイド圏だと仮定すれば、α、λ、ρ（の逆）はほんとうに不要です。