CADG(Categorical Abstract Differential Geometry)の練習問題として、ヤコビ微分圏というモノを考えてます。ヤコビ微分圏は、通常の多変数微分計算のエッセンスを圏論的に取り出したものです。ヤコビ微分圏を考えるに至った動機やご利益について語ります。
内容:
続きの記事:
CADGとデカルト微分圏
CADG(Categorical Abstract Differential Geometry)は、微分や“なめらかさ”の概念を圏論的に定式化して、微分幾何を抽象的に展開する試みです。90年代のリソース・ラムダ計算(resource lambda-calculus, 1993)や80年代のロシツキーの先駆的仕事(Jiri Rosicky, 1984)があったものの、“微分幾何”としての形が整ってきたのは2010年前後でまだ新しい分野です。その有効性と射程はいまだ明らかとは言えません*1。
“微分を持つ圏/なめらかな対象からなる圏”の定義には幾つもの案があります。そのなかでも基本的で重要なものはデカルト微分圏(Cartesian differential category)と接圏(tangent category)です。それぞれの圏(の種別)を最初に提案した論文(基本文献)は以下のものです。
- Title: Cartesian differential categories (2009)
- Authors: R.F. Blute, J.R.B. Cockett, R.A.G. Seely
- Pages: 52p
- URL: http://www.tac.mta.ca/tac/volumes/22/23/22-23abs.html
- Title: Differential structure, tangent structure, and SDG (2013)
- Authors: J.R.B. Cockett, G.S.H. Cruttwell
- Pages: 85p
- URL: https://www.mta.ca/uploadedFiles/Community/Bios/Geoff_Cruttwell/sman3.pdf
デカルト微分圏に関しては、オリジナルから少し変更した一般化デカルト微分圏(generalized Cartesian differential category)をクラットウェルが定義しています。次の論文に記述があります。
- Title: Cartesian differential categories revisited (2012)
- Author: G.S.H. Cruttwell
- Pages: 17p
- URL: https://arxiv.org/abs/1208.4070
- Title:Forms and exterior differentiation in Cartesian differential categories (2013)
- Author: G.S.H. Cruttwell
- Pages: 22p
- URL: http://emis.icm.edu.pl/journals/TAC/volumes/28/28/28-28abs.html
上記の2つの論文のあいだで、一般化デカルト微分圏の定義が少し違っていますが、気にする程の違いではありません。それより、オリジナルのデカルト微分圏(ブルート/コケット/シーリー 2009)と一般化デカルト微分圏(クラットウェル 2013)の関係がハッキリしないほうが問題です。
どうも、一般化デカルト微分圏がオリジナルのデカルト微分圏を完全には包含してないように思えます(下図)。
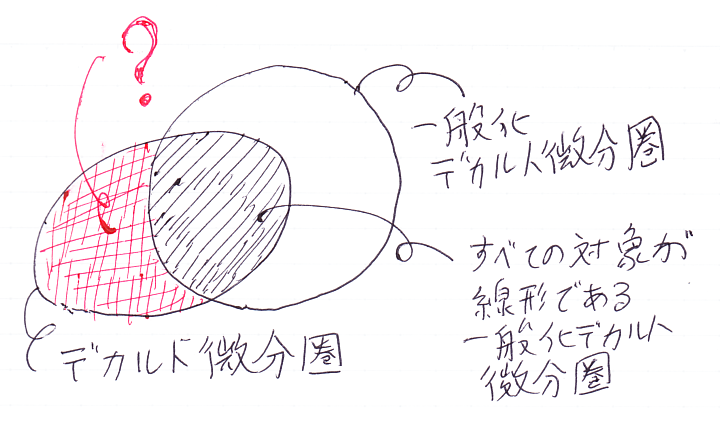
一般化デカルト微分圏のなかで「すべての対象が(クラットウェルの意味で)“線形”である圏」は間違いなく(ブルート/コケット/シーリーの)デカルト微分圏になります。しかし、デカルト微分圏が必ず一般化デカルト微分圏になる保証はなく、「デカルト微分圏だが一般化デカルト微分圏にならない圏」が存在する可能性があります。とはいいながら、僕はその実例を知らないのですが。
仮に「デカルト微分圏だが一般化デカルト微分圏にならない圏」が在ったにしても、一般化デカルト微分圏のほうが使い勝手がいい定義なので、僕は一般化デカルト微分圏を採用します*2。と、そんな事情で、以降、単にデカルト微分圏と言ってもそれはクラットウェルの一般化デカルト微分圏のことです。
デカルト微分圏は、ユークリッド空間における微分計算の抽象的な定式化です。一方、接圏は、なめらかな多様体の圏から抽象した構造です。デカルト微分圏には必ず接圏の構造を入れられます。さらに、デカルト微分圏に制限構造(restriction structure)を載せて、グロンディ(Marco Grandis)の多様体完備化(manifold completion)すると接圏が出来ることもわかっています。また、適当な仮定のもとで接圏は局所的なデカルト微分圏構造を持ちます*3。
以上のことから、「デカルト微分圏 : 接圏」の関係は、「多変数の微分計算 : 多様体の微分幾何」の関係と同様だと言えます。CADGの主要な対象物は接圏ですが、その初等理論、局所理論としてデカルト微分圏の理論がある、という状況ですね。
ヤコビ微分圏の動機
f:Rn→Rm をなめらかな写像だとして、一点でのfの微分係数はm行n列のヤコビ行列(Jacobian matrix)で与えられます。CADGでもヤコビ行列の対応物はあるのでしょうか。…… それがないのです。ヤコビ行列の対応物を作るのは可能なのですが、実際には、ヤコビ行列による定式化は採用されていません。その理由は(おそらく)、行列の対応物を作るのが面倒だからでしょう。行列概念なしでも微分計算は可能だし、そのほうが話が単純になります。
「ヤコビ行列を作るのは七面倒くさいだけでいいことないのか?」と疑問に思い、ちょっと試してみました。確かに面倒くさいです。が、いいこと(メリット、見返り)もあります。ヤコビ行列を使った定式化のいいところを挙げてみます。
- 通常の多変数微分計算の直接的な定式化である。
- 教育的な意義がある。
- 論理との関係が見える。
- 下部構造が面白い。
- 非関手的・非自然な手法が活躍する。
これらのいいことを順に説明していきます。以下では、ヤコビ行列を使った微分をヤコビ微分(Jacobian differential)、ヤコビ微分を備えた圏をヤコビ微分圏(Jacobian differential category)と呼ぶことにします。
通常の多変数微分計算の直接的な定式化である。
ほとんどの多変数微積分の教科書では、多変数の微分係数・導関数をヤコビ行列により定義していると思います。ですから、ヤコビ行列ベースの定式化は我々が慣れ親しんだシナリオをたどることになり、分かりやすいと思います。ヤコビ微分圏は、通常の微分計算をそのまま圏論フレームワーク内に移します
教育的な意義がある。
CADGでは、位相や極限に関する事は扱いません。これにより、微積分や微分幾何のなかで、何が位相・極限に依存して、何が代数計算だけで出来るのかが明確に切り分けられます。これは教育的に意義がありますが、通常の微分計算/微分幾何と異なったシナリオではピンと来ないでしょう。一番目のメリットである「普通さ」があるヤコビ微分圏なら、「切り分け」も意識しやすくなります。
論理との関係が見える。
僕が「おやっ」と思ったのは、ヤコビ微分圏内の微分計算の公式が命題論理の演繹(公理や推論規則)に対応していることです。含意記号を'⊃'として、微分公式に対応するめぼしい演繹を書くと:
*(前提なし)
-----[同一律]
A⊃A
A A⊃B
--------[モダス・ポネンス]
B
A⊃B B⊃C
-----------[カット]
A⊃C
A⊃(B⊃C)
------------
B⊃(A⊃C)
A⊃B C⊃D
--------------
(A∧C)⊃(B∧D)
A
----------
(A⊃B)⊃Bこれらの演繹が微分公式に対応していることは、行列概念(の圏論的対応物)とヤコビ微分を導入しないと見えてこないと思います。
下部構造が面白い。
ヤコビ微分を導入する前に、土台になる圏を整備しなくてはなりません。その圏は、デカルト圏にさらに構造が載ったものです。圏全体はデカルト圏で、特定された部分圏には余デカルト構造が入り半加法圏となっています(次節で記述)。このような構造には(僕は)初めて出会いました。それ自身、なかなか興味深いです。
非関手的・非自然な手法が活躍する。
以下に挙げる過去記事(割と最近)で、非関手的・非自然な手法を説明しました。それらの手法の構成素には、圏論的モダリティ、圏論的コンストラクタ、圏論的オペレータなどがあります*4。
前段落で述べた「外側のデカルト圏と半加法的な部分圏」という構造を定義するには、圏論的モダリティが便利です。また、圏の対象Xにその線形化(linearization; または線形台 linear carrier)という対象L(X)を対応させる操作は圏論的コンストラクタです。圏上のヤコビ微分は圏論的オペレータになります。ヤコビ微分圏は、非関手的・非自然な手法が活躍する事例としての意味があります。
準半加法圏など
ヤコビ微分圏の定義・構成が面倒になる理由は、下部構造の圏が単なるデカルト圏では済まないからです。ヤコビ微分圏の土台になる圏を準半加法圏(qusi-semiadditive category)と呼ぶことにします。「準半」て何だよそれ? と言われそうですが、「準半」に前例がないわけでもありません。
なんでこんな変な名前を付けざるを得ないのか? 「「余」と「双」の使い方がバラバラ」で愚痴ったことがありますが、「双デカルト圏」、「加法圏」、「半加法圏」のあたりは、圏論の定義と用語法が腐っているところで、混乱必至。ですが、致し方ないので慣用の用語法に従うとすると、双積(biproduct)を持つ圏が半加法圏(semiadditive category)となります -- これはろくでもないネーミングだと思うんだけど…
それで、ヤコビ微分圏のために必要な圏は、一部分だけが半加法圏となっているデカルト圏です。「一部分だけ」を表す言葉にpartialがあるので、"partially semiadditive category"とかでも良さそうですが、partial/partiallyは、「偏微分」の「偏」として「複数変数のなかの特定変数に関してだけ」の意味で使いたいので温存したい。で、「完全には半加法圏ではない」から"quasi"を前置して"qusi-semiadditive category"=「準半加法圏」になったわけ。トホホホ。
準半加法圏は部分圏(充満部分圏ではない)として半加法圏を持つので、この半加法的部分圏のなかで線形代数ができます。次のような言葉の置き換えをすればイメージが掴めるでしょう。
- 半加法的部分圏の対象 → ベクトル空間
- 半加法的部分圏の射 → 線形写像
実際クラットウェルは、現状の用語法は無視して、半加法的対象と射を「線形対象」「線形射」と呼んでいます -- それもアリかも知れません。(現状の用語法に拘らないなら、準半加法圏は準線形デカルト圏であり、線形部分圏を持つ、と言えます。)
まーともかく、準半加法圏は、線形代数ができる部分圏(半加法圏)を持つわけです。しかし、行列概念の定義にはデカルト閉構造(の変種)も必要です。閉構造は外側のデカルト圏全体に存在するわけではなくて、半加法的部分圏が閉構造を持つのです。うーん、「閉」をどこに付けたらいいのかな? 準閉半加法圏? 閉準半加法圏? 準半加法閉圏? ハァー(ため息)、現状の用語法に合わせるのも限界かも。
ヤコビ微分圏の抽象的構成・具体的構成
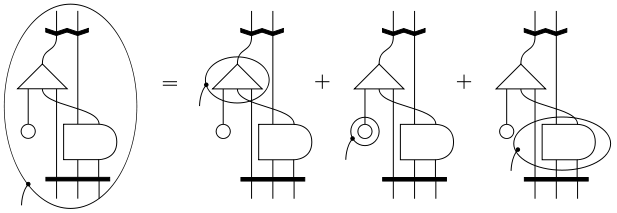
前節で述べたように、ヤコビ微分圏の面倒な部分は土台になる圏の構成です。逆に言うと、土台になる圏を構成してその性質を十分調べておけば、微分オペレータは割と簡単です。古典的微分計算と対応付けたり、絵による微分計算(微分絵算)も出来るでしょう。
絵図主義者(picturalist)には朗報なんですが、微分圏は絵算と意外に相性がいいです。絵算の創始者の一人であるペンローズは、テンソルの代数計算だけでなく、テンソル場の微分計算も(ペンローズ・ヒエログリフとも呼ばれる)彼の図式法で遂行していたので、微分も絵で描けることもむべなるかなです。
ヤコビ微分圏の典型的な事例は、ユークリッド空間の開集合と、その上で定義された無限回微分可能写像の圏です。各点のヤコビ行列により導関数/微分オペレータを定義します -- これがまさにヤコビ微分です。この事例をうまく説明し、今まで見えにくかった構造に光を当てることが出来れば、ヤコビ微分圏の最初の目標はクリアしたと言えるでしょう。
ここまで、ヤコビ微分圏のご利益や周辺事情やロードマップを述べましたが、実質的内容には踏み込んでいません。たぶん、引き続く記事で(いつか)実際のところを話すと思います。一番の難所は錯綜した用語法の整理と選択かも知れません。
続きの記事:
*1:現状では、キラーアプリケーションが見当たりません。めざましい応用例がないと、「ちょっと面白かったけど、結局、役に立たなかったね」となる危惧もあります。
*2:僕の感覚では -- つまり、合理的な説明がうまく出来ないのですが -- オリジナルのデカルト微分圏の定義は良くない、と思えます。使い勝手が悪いだけでなく、なにか外している感覚があります。
*3:これらのことを手っ取り早く知りたいなら、次のスライドがあります。Differential Join Restriction Categories, Differential Categories to Tangential Structure, Tangent categories are locally Cartesian differential categories
*4:他に関連記事として、「余可換コモノイド・モダリティ事件の解説」、「天空の支配者」。
*5:画像は、Wikipedia項目"Penrose_graphical_notation"より