最近、ラックス・モノイド関手の記述と計算のためにサーフェイス図を描いているのですが、サーフェイス図をきれいに描いて公開するのは手間がかかり過ぎて無理です。致し方ないのでテキストで表示しますが、3次元的情報をシリアライズしたテキストは、書くのも読むのも困難です。折衷案として、2次元的にレイアウトしたテキストで3次元サーフェイス図の情報を表すことにします。$`\newcommand{\id}{\mathrm{id}}
\newcommand{\twoto}{\Rightarrow}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\In}{\text{ in } }
\newcommand{\Id}{\mathrm{Id}}
\newcommand{\ID}{\mathrm{ID}}
\require{color}
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
`$
内容:
サーフェイス図
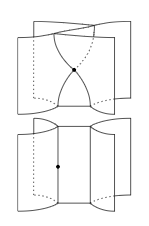
サーフェイス図は、3次元空間内の点、曲線、曲面を組み合わせた図形で、2-圏や3-圏内の高次射を表すものです。例えば、次の図は、上下に並べられた2つのサーフェイス図を縦結合しようとしている状況です。
当面必要なのは、圏達の2-圏 $`{\bf CAT}`$ 内の射(0-射、1-射、2-射)を表すサーフェイス図です。面〈ウォール〉が0-射〈圏〉、線〈ワイヤー〉が1-射〈関手〉、点〈ノード〉が2-射〈自然変換〉を表すことになります。
サーフェイス図は、3次元方体〈キューブ〉であるキャンバス空間内に描かれます。3次元キャンバス空間の座標軸を次のように定めます。
- x-軸 : 左から右、直積(記号 ×)(より一般にはモノイド積)はこの方向とする。
- y-軸 : 奥から手前、横結合(記号 *)はこの方向とする。
- z-軸 : 上から下、縦結合(記号 ;)はこの方向とする。
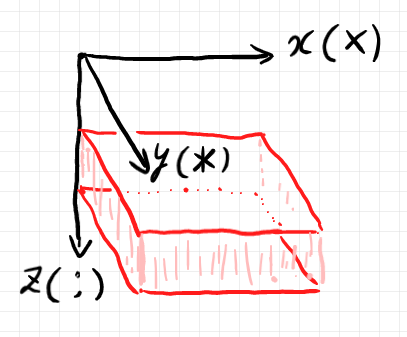
xy-平面と平行な平面をカット面〈cut plane〉と呼ぶことにします(図の赤枠の面)。2枚のカット面で挟まれた方体〈キューブ〉はスライス〈slice〉と呼びましょう(図のピンクの箱)。
サーフェイス図のテキスト化の基本的な手段は、キャンバス方体を(n + 1)枚のカット面で切り分けて、n個のスライスを作ることです。カット面による2次元断面図とスライス内の“薄いサーフェイス図”をそれぞれテキスト表示します。
1斤の塊の食パンを、スライスに切り分けて食べやすくするのと同じです。
実例
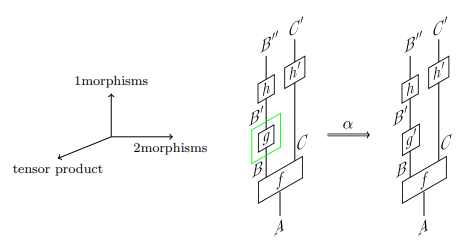
次はバートレット〈Bruce Bartlett〉による絵です。
座標軸の約束は前節で述べたものとは違います。もし、右側に観測者がいるなら、その人から見て:
- tensor product 軸 :右から左(左から右ではない)
- 1morphism 軸 : 下から上
- 2morphism 軸 : 奥から手前
どうテキスト化するかは、演算子記号が図式順か反図式順かにより変わります。バートレットは次の約束です(我々とは違います)。
- テンソル積〈モノイド積〉の記号は '$`\otimes`$' 、反図式順で、右〈プレ〉の因子は右に書く。
- 結合の記号は '$`\cdot`$' 、反図式順で、下〈プレ〉の因子は右に書く。
- 縦結合の記号は '$`\circ`$' 、反図式順で、手前〈プレ〉の因子は右に書く。
この約束で2つの2次元ストリング図は次のようにテキスト化されます。
- $`(h \otimes h')\cdot (g \otimes \id_C) \cdot f`$
- $`(h \otimes h')\cdot (g' \otimes \id_C) \cdot f`$
奥から手前を左から右に書き換えると($`f`$ の下に2本ワイヤーは間違いですね):
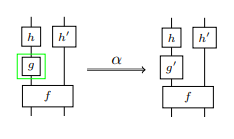
$`\alpha`$ は次のようにテキスト表示できます。
$`\quad (h \otimes h')\cdot (g \otimes \id) \cdot f \overset{\alpha}{\twoto} (h \otimes h')\cdot (g' \otimes \id) \cdot f`$
図のレイアウトとテキスト配置が一致していますが、それは、図のテンソル積を右から左、図の横結合を下から上と決めて、書字方向の逆転(右がプレ、左がポスト)を相殺するように細工しているからです。
経験上、方向の逆転操作の小細工はストレス/混乱の原因になるので、我々は次の方針とします。
- 自然な書字方向である「左から右」「上から下」と演算のプレ因子/ポスト因子の配置を一致させる。
- テキストの書字方向と図のレイアウトを一致させる。つまり、テキストの左は図でも左、テキストの上は図でも上。
- ただし、奥から手前の方向は如何ともし難いので、次元を潰してテキスト・エンコードする。
我々の方針に従うなら、バートレットの例は次のようにテキスト表示します。
$`
\quad f * (\id_C \otimes g ) * (h' \otimes h)\\
\quad \Downarrow \alpha\\
\quad f * (\id_C \otimes g' ) * (h' \otimes h)
`$
ここで、$`f * (\id_C \otimes g ) * (h' \otimes h)`$ は、本来2次元の情報を1次元に押し込めているのですが、上から見た2次元情報(y-軸が上から下に見える)を2次元テキスト配置で示せば:
$`
\quad A\\
\quad \downarrow f \\
\quad C \otimes B \\
\quad \downarrow \id_C \otimes g\\
\quad C \otimes B'\\
\quad \downarrow h' \otimes h\\
\quad C' \otimes B''
`$
上から見ると、奥が上、手前が下に見えるわけです。テンソル積は相変わらず左から右に見えています。
必要があれば、3次元サーフェイス図の2次元断面を2次元テキスト配置で書きますが、通常は1次元テキスト配置〈シリアライズ形式〉で表現します。1-射のプロファイル(奥と手前の境界情報)を添えると、分かりやすさが向上します。
$`
\quad f * (\id_C \otimes g ) * (h' \otimes h) : A \to C' \otimes B''\\
\quad \Downarrow \alpha\\
\quad f * (\id_C \otimes g' ) * (h' \otimes h) : A \to C' \otimes B''
`$
ラックス・モノイド関手からの例
ラックス・モノイド関手 $`(F, \nu, \iota)`$ の結合律は、左辺・右辺を2-射〈自然変換〉とする等式です。その左辺になる2-射をテキスト表示してみます。$`{\bf CAT}`$ に対するサーフェイス図からテキストへの翻訳と考えます。
まず、$`\nu`$ は次のように表せます。$`P, Q`$ はモノイド積(双関手)です。
$`\For \cat{C}, \cat{D} \In {\bf CAT}\\
\For P:\cat{C}\times \cat{C} \to \cat{C} \In {\bf CAT}\\
\For Q:\cat{D}\times \cat{D} \to \cat{D} \In {\bf CAT}\\
\For F:\cat{C} \to \cat{D} \In {\bf CAT}\\
\:\\
\quad (F \times F) * Q : \cat{C}\times \cat{C} \to \cat{D}\\
\quad \Downarrow \nu \In {\bf CAT}\\
\quad P*F : \cat{C}\times \cat{C} \to \cat{D}
`$
横1行で書けば:
$`\quad \nu :: (F \times F) * Q
\twoto P*F : \cat{C}\times \cat{C} \to \cat{D} \In {\bf CAT}
`$
念のため、$`\nu`$ の域と余域である関手を2次元的配置で書けば:
$`
\quad \cat{C} \times \cat{C} \\
\quad \downarrow F \times F \\
\quad \cat{D} \times \cat{D}\\
\quad \downarrow Q \\
\quad \cat{D}\\
\:\\
\quad \cat{C} \times \cat{C} \\
\quad \downarrow P \\
\quad \cat{C}\\
\quad \downarrow F \\
\quad \cat{D}
`$
ラックス・モノイド関手の結合律の左辺を書き下してみます。次の点には注意してください。
- 見やすくするためにブラケット〈角括弧〉も使うが、丸括弧と意味は変わらない。
- $`{\bf CAT}`$ の等式的法則による変形も記すが、等式的変形は $`\Updownarrow`$ で表す。
- 1-射〈関手〉の恒等2-射〈恒等自然変換〉は、1-射と同じ書き方をする。2-射が出現する文脈に1-射が出現したら、対応する恒等2-射と解釈する。
$`
\quad [( (F\times F)\times F)*(Q \times \Id_\cat{D} )]* Q \\
\quad \Updownarrow [\text{interch}_{F\times F, F, Q, \Id_\cat{D}}] * Q \\
\quad [( (F\times F)*Q ) \times F * \Id_\cat{D} ] * Q \\
\quad \Updownarrow [( (F\times F)*Q ) \times \text{runit}_{F} ] * Q\\
\quad [ (F\times F)*Q ) \times F ] * Q \\
\quad \Downarrow [ \nu \times F ] * Q\\
\quad [ (P*F) \times F ] *Q \\
\quad \Updownarrow [ (P*F) \times \text{lunit-inverse}_{F} ] * Q\\
\quad [ (P*F) \times (\Id_{C} * F) ]*Q \\
\quad \Updownarrow [\text{interch-inverse}_{P, F, \Id_\cat{C}, F}] *Q\\
\quad [ (P \times \Id_\cat{C}) * (F \times F) ] *Q\\
\quad \Updownarrow \text{assoc}_{P \times \Id_\cat{C}, F \times F, Q}\\
\quad (P \times \Id_\cat{C}) * [(F \times F) *Q]\\
\quad \Downarrow (P \times \Id_\cat{C}) * [\nu]\\
\quad (P \times \Id_\cat{C}) * [ P * F]\\
\quad \Updownarrow \text{assoc-inverse}_{P \times \Id_\cat{C}, P, F}\\
\quad [ (P \times \Id_\cat{C}) * P] * F\\
`$
等式的変形ではない部分だけを抜き出して横一行で表示すれば次のようです。恒等自然変換は明示的に書いています。アスタリスクはヒゲ結合〈whiskering〉です。
$`\quad
[( \nu \times \mathrm{ID}_F ) * Q] \mathop{;} [(P \times \Id_\cat{C}) * \nu]
`$