昨日書いた記事「サーフェイス図のテキスト表現」に、少し続きがあります。$`\newcommand{\twoto}{\Rightarrow}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\In}{\text{ in } }
\newcommand{\Id}{\mathrm{Id}}
\newcommand{\C}{\mathop{;}}
\newcommand{\ID}{\mathrm{ID}}
\newcommand{\id}{\mathrm{id}}
`$
内容:
キャンバスとプロファイル
圏達のデカルト厳密2-圏 $`({\bf CAT}, \times, {\bf 1})`$ におけるサーフェイス図〈3次元ストリング図〉の話です。この2-圏*1におけるサーフェイス図は、2-射〈自然変換〉を表します。サーフェイス図が描かれる場所である3次元キャンバスは、実数単位区間 $`[0, 1]`$ の直積である $`[0, 1]^3`$ であると仮定します。この仮定はまったく便宜上のもので必然性はありません。座標軸の取り方は昨日の記事のとおりです(図再掲)。
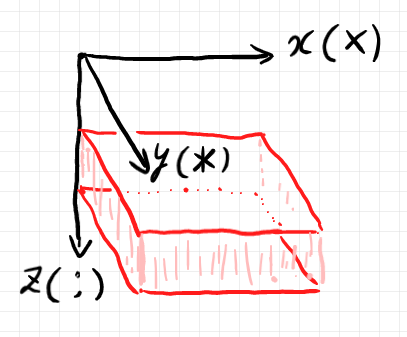
キャンバス方体〈キューブ〉の z = 0 の面を上面、z = 1 の面を下面と呼ぶことにします。また、y = 0 の面を奥面、y = 1 の面を手前面だとしましょう。このような呼び方も単なる符丁で、便宜上の約束に過ぎません。が、名指しのために約束は必要です。
キャンバスの上面だけ見ると、2次元キャンバスに描かれたストリング図になります。このストリング図は2-圏 $`{\bf CAT}`$ の1-射、つまり関手を表します。キャンバスの下面にも関手が描かれています。上面の関手と下面の関手が、サーフェイス図の自然変換の域・余域を与えます。サーフェイス図が表す自然変換が $`\alpha`$ 、上面の関手が $`H`$ 、下面の関手が $`H'`$ ならば、次のようなプロファイル記述が書けます。
$`\quad \alpha :: H \twoto H' \In {\bf CAT}`$
キャンバスの奥面だけ見ると、縦線が何本か引かれているはずです。縦線は圏で、何本かの縦線は直積された圏だと解釈できます。例えば、$`\cat{C}, \cat{D}`$ の縦線が(左から右に)並んでいたら、圏 $`\cat{C}\times \cat{D}`$ を表します。奥面の圏と手前面の圏が、“サーフェイス図の自然変換の域・余域”の域・余域を与えます。上面の関手 $`H`$ と下面の関手 $`H'`$ は、域・余域である圏を共有するので、それを $`\cat{A}, \cat{B}`$ とすれば、次のようなプロファイル記述が書けます。
$`\quad \alpha :: H \twoto H' : \cat{A} \to \cat{B} \In {\bf CAT}`$
テキストでもz方向を上から下にしたいなら(y方向が左から右):
$`\quad
\alpha ::
\begin{matrix}
H:\cat{A} \to \cat{B}\\
\Downarrow \\
H':\cat{A} \to \cat{B}\\
\end{matrix}
\In {\bf CAT}
`$
自然変換方体
デカルト厳密2-圏 $`({\bf CAT}, \times, {\bf 1})`$ において解釈をする前提で、内部にサーフェイス図が描かれた3次元キャンバス方体は、自然変換を表すので自然変換方体〈natural transformation cube〉と呼ぶことにします。自然変換方体は六面体ですが、表面に描かれた“模様”は次の意味です。
- 上面の模様は、自然変換の域である関手のストリング図(ワイヤーとノードの組み合わせ)
- 下面の模様は、自然変換の余域である関手のストリング図(ワイヤーとノードの組み合わせ)
- 奥面の模様は、自然変換の域・余域である関手の域の圏の図(縦線の並び)
- 奥面の模様は、自然変換の域・余域である関手の余域の圏の図(縦線の並び)
- 左面は模様なし〈無地〉
- 右面は模様なし〈無地〉
自然変換の演算は、自然変換方体をくっつくて並べる操作になります。
- 2つの自然変換方体をx軸方向に並べると、自然変換の直積
- 2つの自然変換方体をy軸方向に並べると、自然変換の横結合
- 2つの自然変換方体をz軸方向に並べると、自然変換の縦結合
くっつくて並べる場合に、くっつける面の模様が一致している必要があります。
- 2つの自然変換方体をx軸方向に並べる〈直積する〉とき、第一の方体の右面と第二の方体の左面の模様が一致する必要がある。が、どちらも無地なので実際は無条件。
- 2つの自然変換方体をy軸方向に並べる〈横結合する〉とき、第一の方体の手前面と第二の方体の奥面の模様が一致する必要がある。
- 2つの自然変換方体をz軸方向に並べる〈縦結合する〉とき、第一の方体の下面と第二の方体の上面の模様が一致する必要がある。
演算が可能かどうかの判断は、表面の模様だけ見ればいいので、自然変換方体の中身を見る必要はありません。中身が見えないブラックボックスであっても正しく演算して組み合わせることができます。組み合わせに必要な情報はプロファイル(自然変換のインターフェイス)だけです。
表面に模様が描いてある方体〈キューブ〉を3つの方向に並べるという比喩(メンタルモデル)は、非常に直感的で、複雑なデカルト2-圏の演算を馴染みやすくしてくれます。このような発想と手法は、一部では昔から使われています。次の図は、ギロー〈Yves Guiraud〉の "The three dimensions of proofs" にある図です。
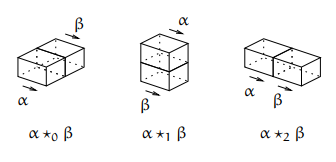
$`\star_0, \star_1, \star_2`$ という記号で表される3つの演算があり、それぞれが空間の3方向に対する“くっつくて並べる操作”で描かれています。
演算が2つの場合でも、その描画方向の選び方は人によりバラバラです(下の過去記事参照)。演算が3つの場合ならなおさら、描画方向の選び方は人によりバラバラとなるでしょう。描画方向の組み合わせ方がより多いので、さらに混沌としたことになりますね(頭痛)。
関手の縦伸ばし
サーフェイス図を使って記述や計算をしていると、関手のストリング図を縦方向〈z方向〉に引き伸ばして自然変換として使いたいことがあります。これは単に恒等自然変換を作ればいいだけですが、テキスト表現に少し注意が必要です。
2-圏 $`{\bf CAT}`$ では「恒等」が何種類もあります。
- 圏 $`\cat{C}`$ の対象 $`A`$ の恒等射 $`A \to A \In \cat{C}`$
- 圏 $`\cat{C}`$ の恒等関手 $`\cat{C} \to \cat{C} \In {\bf CAT}`$
- 関手 $`F`$ の恒等自然変換 $`F \twoto F \In {\bf CAT}`$
同じ $`\id_-`$ だと混乱してしまうで、次のように書き分けることにします。
- 圏 $`\cat{C}`$ の対象 $`A`$ の恒等射 $`\id_A: A \to A \In \cat{C}`$
- 圏 $`\cat{C}`$ の恒等関手 $`\Id_\cat{C} : \cat{C} \to \cat{C} \In {\bf CAT}`$
- 関手 $`F`$ の恒等自然変換 $`\ID_F :: F \twoto F \In {\bf CAT}`$
恒等自然変換 $`\ID_F`$ を関手圏 $`{\bf CAT}(\cat{C}, \cat{D})`$ の1-射とみなすときは $`\id_F`$ か $`\ID_F`$ か悩みますが、まー、どっちでもいいでしょう。
「恒等」の域・余域を下付きにするのが習慣ですが、この記法はあまり良くありません。入れ子の下付きになったりすると(そうでなくても)視認性が悪いです。次の書き方がベターだと思います。
- 圏 $`\cat{C}`$ の対象 $`A`$ の恒等射 $`{^\id}[A]: A \to A \In \cat{C}`$
- 圏 $`\cat{C}`$ の恒等関手 $`{^\Id}[\cat{C}] : \cat{C} \to \cat{C} \In {\bf CAT}`$
- 関手 $`F`$ の恒等自然変換 $`{^\ID}[F] :: F \twoto F \In {\bf CAT}`$
例えば、$`(F\times \Id_\cat{C})*P : \cat{C}\times \cat{C} \to \cat{C}`$ を縦伸ばしした恒等自然変換は次のように書けます。
$`\quad {^\ID}[(F\times {^\Id}[\cat{C}])*Q] :: {^\Id}[\cat{C}\times \cat{C}] \twoto {^\Id}[\cat{C}] : \cat{C}\times \cat{C} \to \cat{C}`$
従来の書き方だと、だいぶ視認性が悪いです。
$`\quad \ID_{(F\times \Id_\cat{C} )*Q } :: \Id_{\cat{C}\times \cat{C} } \twoto \Id_{\cat{C}} : \cat{C}\times \cat{C} \to \cat{C}`$
「めんどくさい/鬱陶しい」という理由で、関手とその恒等自然変換を区別しないでオーバーロードすることがしばしばあります。ヒゲ結合〈whiskering〉$`F * \alpha`$ は、$`{^\ID}[F]*\alpha`$ を横着して書いたとみなせます*2。
関手と恒等自然変換のオーバーロードは確かに便利なんですが、混乱の原因にもなるのでホドホドにしたほうがいいでしょう。絵図では、関手は2次元矩形に描かれるストリング図で、自然変換は3次元方体に描かれるサーフェイス図です。文字通り「次元が違う」ので、同一視はまずいです。
サーフェイス図のテキスト表現の話はまだ続くかも知れない。