このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

圏論的述語論理とお絵描き

雑記／備忘

圏論的述語論理の話は過去に何度かしたことがありますが、現時点での観点から大雑把に復習してみます。そして、「全称記号の導入」と「存在記号の消去」と呼ばれる“推論規則”の絵の描き方を紹介します。$`
\newcommand{\Imp}{\Rightarrow }
\newcommand{PPB}{\diamondsuit} % Predicate Pull Back
\newcommand{\cat}[1]{\mathcal{#1} }
\newcommand{\op}{\mathrm{op} }
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\In}{\:\text{ in } }
\newcommand{\id}{\mathrm{id} }
\require{color}
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
\newcommand{\Define}{\Keyword{Define } }%
\newcommand{\Where}{\Keyword{Where } }%
`$

内容：

シリーズ記事：

  1. 述語論理： ベース圏と論理代数の圏
  2. 述語論理： カリー／ハワード／ランベック対応と推論・型つけ規則
  3. 述語論理： 様々な多圏達の分類整理
  4. 述語論理： 二重圏的ハイパードクトリン
  5. 述語論理： シード付き二重圏 -- 訂正と再論

関連記事：

  1. 自然言語混じり形式証明の意味論と最近の型理論

ハイパードクトリン

述語論理とは、限量子も扱う論理です。命題論理でも述語は扱うので、“述語を扱う論理”という意味ではありません（言葉に騙されないように）。述語論理の圏論的定式化といえば、ローヴェア〈William Lawvere〉のハイパードクトリンでしょう。ハ・イ・パー・ド・ク・ト・リ・ン -- あー、なんか言うの気恥ずかしい。ローヴェアが案出した用語はどうも使いにくいものが多いですね（algebraic theory も rig もそう）。しかし、代わりの言葉もないので「ハイパードクトリン」を使います。

ハイパードクトリンは、デカルト閉圏 $`\cat{C} = (\cat{C}, \times, {\bf 1}, [-, -])`$ ともうひとつ何らかの圏 $`\cat{L}`$ 、そして反変関手 $`\mrm{Pred}`$ からなります。'Pred' は predicate からです。

$`\quad \mrm{Pred}:\cat{C}^\op \to \cat{L} \In {\bf CAT}`$

$`X\in |\cat{C}|`$ に対する関手の値は $`\mrm{Pred}[X]`$ と書きます（ブラケット使います）。

$`\mrm{Pred}[X]`$ は、代数的・順序的構造を持ちます。その構造の例としては：

  1. 順序集合
  2. ハイティング代数
  3. ブール代数
  4. デカルト閉圏

ここでは、$`\mrm{Pred}[X]`$ はデカルト閉圏であり、さらに余完備（cocomplete）であるとします。つまり、$`\cat{L}`$ は余完備デカルト閉圏の圏*1で、$`\mrm{Pred}[X]`$ は余完備デカルト閉圏です。

$`\mrm{Pred}[X]`$ が“とてもやせている”〈very thin〉場合は、$`\mrm{Pred}[X]`$ は完備ハイティング代数になります。ここで、圏が“とてもやせている”とは次の2つの条件を満たすことです。

  1. すべてのホムセットは、要素をたかだか1個しか持たない。（thin条件）
  2. 2つの対象が同型なら、その2つの対象は等しい。（gaunt条件）

圏 $`\cat{C}`$ も圏 $`\mrm{Pred}[X]`$ もデカルト閉圏なので、混乱のリスクがあります。$`\mrm{Pred}[X]`$ のデカルト閉構造は次のように書いて区別します。

$`\quad \mrm{Pred}[X] = (\mrm{Pred}[X], \land, \top, \Imp)`$

もっとも、今日のところはデカルト閉構造は使いませんが。

$`(\cat{C}, \cat{L}, \mrm{Pred})`$ がハイパードクトリンであるための条件はまだあります。それについては、節を改めましょう。

ところで、ハイパードクトリンに関するテキストとしては、次が読みやすいと思います。この記事も、おおよそこのテキストに従っています。

随伴による限量子の定義

$`(\cat{C}, \cat{L}, \mrm{Pred})`$ がハイパードクトリンであるための条件について説明を続けます。$`\cat{C}`$ はデカルト閉圏（当然にデカルト圏）なので、次のような射影があります。

  • $`\pi^1_{X, Y}: X\times Y \to X \In \cat{C}`$
  • $`\pi^2_{X, Y}: X\times Y \to Y \In \cat{C}`$

第一射影に注目して、単に $`\pi_{X, Y}`$ と書いたらそれは第一射影のことだとします。

$`\mrm{Pred}`$ は反変関手だったので、$`\pi_{X, Y}`$ に $`\mrm{Pred}`$ を適用すると次の射（余完備デカルト閉圏のあいだの適切な関手）が得られます。

$`\quad \mrm{Pred}[\pi_{X, Y}] : \mrm{Pred}[X] \to \mrm{Pred}[X\times Y] \In \cat{L}`$

得られた射をダイアモンド記号で表すことにします。

$`\For X, Y \in |\cat{C}|\\
\Define \PPB_X^Y := \mrm{Pred}[\pi_{X, Y}]`$

$`\PPB_X^Y`$ は、$`\pi_{X, Y}`$ による述語の引き戻しを意味します。もっと直感的に言うと、$`X`$ 上の述語 $`P(x)`$ に対して、変数の水増しをした述語 $`P'(x, y) = P(x)`$ を対応させることです。

なお、過去の記事（例えば以下）ではダイアモンド記号ではなくて大文字デルタ（三角記号）を使っていました。

$`(\cat{C}, \cat{L}, \mrm{Pred})`$ がハイパードクトリンであるためには、すべての $`\PPB_X^Y`$ に対して右随伴関手と左随伴関手の存在が要請されます。述語論理としての意味付けは：

  • $`\PPB_X^Y`$ の右随伴関手が全称限量子 $`\forall_X^Y`$ である。
  • $`\PPB_X^Y`$ の左随伴関手が存在限量子 $`\exists_X^Y`$ である。

関手の随伴ペアがあれば、ホムセットのあいだの同型が存在します。それらは次のようです。

$`\quad \mrm{Pred}[X\times Y](\PPB_X^Y(P), Q) \cong \mrm{Pred}[X](P, \forall_X^Y(Q))\\
\quad \mrm{Pred}[X\times Y](P, \PPB_X^Y(Q) ) \cong \mrm{Pred}[X](\exists_X^Y(P), Q)
%`$

左から右に向かう同型写像〈全単射〉を次のように名付けます。

$`\quad
{\forall\text{-Intro}_X^Y}_{P, Q} :
\mrm{Pred}[X\times Y](\PPB_X^Y(P), Q) \to \mrm{Pred}[X](P, \forall_X^Y(Q))\\
\quad
{\exists\text{-Elim}_X^Y}_{P, Q} :
\mrm{Pred}[X\times Y](P, \PPB_X^Y(Q) ) \to \mrm{Pred}[X](\exists_X^Y(P), Q)
%`$

これらがそれぞれ、「全称記号の導入」、「存在記号の消去」です。この形で見るとどっちも導入に思えますが、歴史的事情から、ホムセットの右側に全称記号が入れば「導入」、左側に存在記号が入れば「消去」です。

随伴ペアの同型写像の名前が長いし、添字もイッパイ付いていて鬱陶しいので次のように略記します。

$`\quad
(-)^{\forall I} :
\mrm{Pred}[X\times Y](\PPB_X^Y(P), Q) \to \mrm{Pred}[X](P, \forall_X^Y(Q))\\
\quad
(-)^{\exists E} :
\mrm{Pred}[X\times Y](P, \PPB_X^Y(Q) ) \to \mrm{Pred}[X](\exists_X^Y(P), Q)
%`$

ハイパードクトリンの条件としてさらに、$`\forall_X^Y, \exists_X^Y`$ は $`X`$ に関して自然変換になることが要求されます。そのことを具体的に書けば、$`t:X \to X' \In \cat{C}`$ に対して、次の図式が可換になることです。

$`\require{AMScd}
\begin{CD}
\mrm{Pred}[X' \times Y] @>{ \forall_{X'}^Y }>> \mrm{Pred}[X'] \\
@V{ \mrm{Pred}[t\times \id_Y] }VV @VV{ \mrm{Pred}[t] }V\\
\mrm{Pred}[X \times Y] @>{ \forall_X^Y }>> \mrm{Pred}[X]
\end{CD}\\
\:\\
\begin{CD}
\mrm{Pred}[X' \times Y] @>{ \exists_{X'}^Y }>> \mrm{Pred}[X'] \\
@V{ \mrm{Pred}[t\times \id_Y] }VV @VV{ \mrm{Pred}[t] }V\\
\mrm{Pred}[X \times Y] @>{ \exists_X^Y }>> \mrm{Pred}[X]
\end{CD}\\
\:\\
\text{commutative in }\cat{L}
%`$

この自然性条件は、ベック／シュバレー条件〈Beck-Chevalley condition〉と呼ばれます。

以上が、$`(\cat{C}, \cat{L}, \mrm{Pred})`$ がハイパードクトリン〈hyperdoctrine〉であるための条件です。

入れ子のキャンバスの描き換え

ここからはお絵描きの話です。$`(\cat{C}, \cat{L}, \mrm{Pred})`$ はハイパードクトリンとします。

$`X\in |\cat{C}|`$ に対して、左上に $`X`$ と注記されたキャンバス（2次元有限矩形）を準備します。余完備デカルト閉圏 $`\mrm{Pred}[X]`$ の様子は、“キャンバス $`X`$” に描くと約束します。

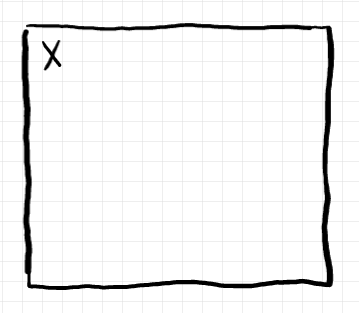
余完備デカルト閉圏 $`\mrm{Pred}[X\times Y]`$ の様子は、まったく別に“キャンバス $`X\times Y`$” を準備してもいいですが、“キャンバス $`X`$” の中に入れ子にしたキャンバスでもよいとしましょう。このとき、外側のキャンバスに $`X`$ と注記しているので、内側のキャンバスには $`Y`$ とだけ書くことにします。

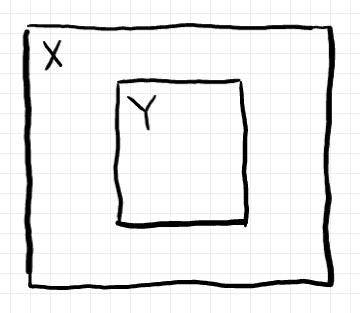
このような約束のもとで、前節のホムセットのあいだの同型写像は次のような描き換えとして表現します。

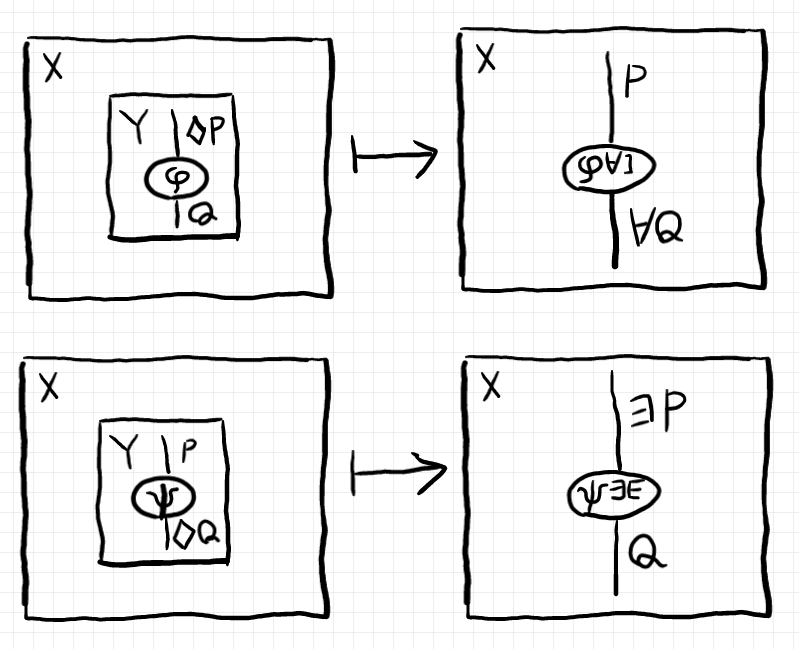
テキストとして写し取るならば：

$`\quad
\mrm{Pred}[X\times Y](\PPB_X^Y P, Q) \ni \varphi \mapsto
\varphi^{\forall I} \in \mrm{Pred}[X]( P, \forall_X^Y Q) \\
\quad
\mrm{Pred}[X\times Y]( P, \PPB_X^Y Q) \ni \psi \mapsto
\psi^{\exists E} \in \mrm{Pred}[X]( \exists_X^Y P, Q)
%`$

描き換えの代わりにマーカーを使う

入れ子のキャンバスをフラットな（入れ子がない）キャンバスに描き換える操作は、絵の時間的な変化〈遷移〉なので、理想を言えばアニメーションにしたいところです。将来的にはアニメーションを利用した表現も出来るかも知れません（「「コミュニケーションの多次元化」という革命に立ち会っているのだと思う」参照）が、現時点では、静的描画法の工夫で絵の時間的な変化〈遷移〉を表しましょう。

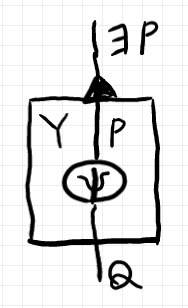
まず、“キャンバス $`X`$” 内のワイヤー $`P`$ と、入れ子にされた“キャンバス $`X\times Y`$”内のワイヤー $`\PPB_X^Y P`$ を同一視します。外側のキャンバスのワイヤー $`P`$ が内側のキャンバスにそのまま貫入するのを許します。内側では実際には $`\PPB_X^Y P`$ ですが、それも $`P`$ として扱います。

同様に、内側の $`\PPB_X^Y Q`$ が外側のキャンバスへと抜け出ていくのを許します。内側の $`P`$ が単純に外側まで伸びた絵を描きます。

次の約束として、内側のワイヤー $`Q`$ が $`\forall_X^Y Q`$ として外側に抜け出るときは、内側キャンバスの下側境界線上にマーカーを描きます。下向き黒三角としましょう。

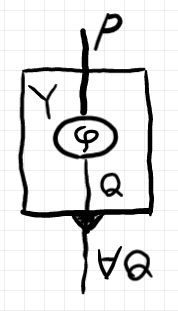
同様に、外側のワイヤー $`\exists_X^Y P`$ が $`P`$ として内側に入り込むときは、内側キャンバスの上側境界線上にマーカーを描きます。上向き黒三角としましょう。

過去の描画法との関係

今紹介した描画法は、以下の過去記事の描画法と本質的には同じです。


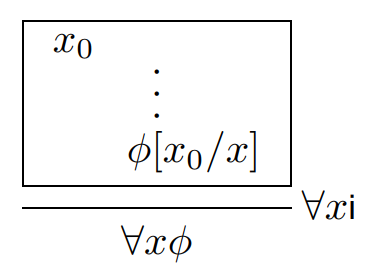
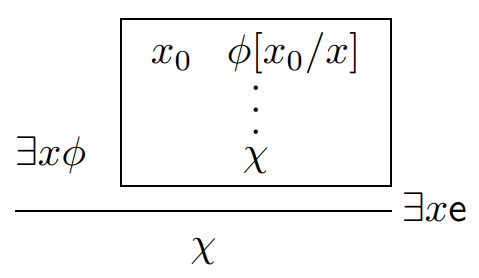
この記事で入れ子のキャンバスとハイパードクトリンとの関係が明らかになり、レイアウトも少しスッキリしたような気がします。

2009年の記事「演繹系とお絵描き圏論」において：

さらに、構造規則は回路図（ボックス＆ワイヤー図、ストリング図）と相性がいいのです。一般的な「n-入力 m-出力」の回路図の全体は、圏というより多圏（polycategory）という構造を作るのですが、お絵描き計算には非常に都合がいい舞台です。

僕が想定しているシナリオでは、ラムダ計算も命題論理もお絵描き（回路図）ありきなので、絵が描きやすいことが最優先の定式化になっているのです。

命題論理にかぎらず述語論理でも（僕にとっては）「絵が描きやすいことが最優先」です。述語論理では、$`\cat{C}`$ の異なる対象の上には異なる述語達の世界が載るので、描画には何枚ものキャンバスが必要で、それらのキャンバスのあいだを $`\PPB_X^Y, \forall_X^Y, \exists_X^Y`$ で行ったり来たりすることになります。どうしても絵が複雑化するのですが、入れ子キャンバスやマーカーを駆使すれば、なんとか絵を描けるのではないかと思っています。

*1:関手だけでなく自然変換も考えれば2-圏になりますが、当面1-圏と考えます。