属性付き2-グラフのスノーグローブ現象 - 檜山正幸のキマイラ飼育記 (はてなBlog)

「属性付き2次元グラフ：図式言語の基本」において、図式、形状、テンプレートについて説明しました。次のように述べました。

形状と図式は違う概念である。
テンプレートは、特別な場合として形状も図式も含む一般的概念である。

ところが次も言えます。

テンプレートは、とある形状の図式である。

そうなると、図式とテンプレートは、お互いに相手を飲み込もうとする関係になります。

図式は、テンプレートの特別な例である。テンプレートは図式を飲み込む。
テンプレートは、図式の特別な例である。図式はテンプレートを飲み込む。

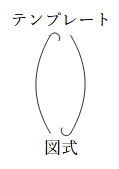
これは循環的構造ですが、循環を展開すると、次のような無限階層になります。

図式を一般化してテンプレートを考える。
テンプレートは図式だ。
図式を一般化してテンプレートを考える。
テンプレートは図式だ。
図式を一般化してテンプレートを考える。
‥‥（繰り返し）

階層をいくらでも登れますが、同じ状況が繰り返し現れます。メタレベルへと階層を登ったのだけど、そこで見える景色は以前と同じ、という不気味な状況なんです。$`\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\mbf}[1]{\mathbf{#1}}
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\msc}[1]{\mathscr{#1}}
\newcommand{\In}{\text{ in }}
%\newcommand{\twoto}{\Rightarrow }
%\newcommand{\op}{\mathrm{op} }
\newcommand{\id}{\mathrm{id}}
%\newcommand{\u}[1]{\underline{#1}}
%\newcommand{\o}[1]{\overline{#1}}
%\newcommand{\hyp}{ \text{－} }
%\newcommand{\Iff}{ \Leftrightarrow }
%\newcommand{\Imp}{ \Rightarrow }
\newcommand{\incto}{\hookrightarrow }
\newcommand{\fibto}{\twoheadrightarrow}
%\newcommand{\SWArrow}{\style{display: inline-block; transform: rotate(-45deg)}{\Leftarrow} }
\newcommand{\T}[1]{\text{#1}}
`$

内容：

形状・図式・テンプレートを定義する形状
スノーグローブ現象
メタな図式の正確な定義
視覚的な修飾の約束
おわりに

形状・図式・テンプレートを定義する形状

「コラージュ図式：圏論的判断計算の主要な道具」で問題図式〈コラージュ図式テンプレート〉と解図式を説明するために図式を使っています。

問題図式を説明する図式：

$`\quad \xymatrix@C+1pc{
{S_\mrm{giv}} \ar@{~>}[dr]^{G} \ar@{_{(}->}[dd]_S
&{}
\\
{}
&{\msc{T}}
\\
{S_\mrm{tot}}
&{}
}
`$

解図式を説明する図式：

$`\quad \xymatrix@C+1pc{
{S_\mrm{giv}} \ar@{~>}[dr]^{G} \ar@{_{(}->}[dd]_S
\ar@{}@/^1.5pc/[dd]|{\text{comm.}}
&{}
\\
{}
&{\msc{T}}
\\
{S_\mrm{tot}} \ar@{~>}[ur]_{E}
&{}
}
`$

ラベルをすべて削除して、形状〈shape〉を表わす頂点は黒丸、ターゲット・ドクトリンを表わす頂点はダイヤモンド形にします。

問題図式の図式の形状：

$`\quad \xymatrix@C+1pc{
{\bullet} \ar@{~>}[dr] \ar@{_{(}->}[dd]
&{}
\\
{}
&{\diamond}
\\
{\bullet }
&{}
}
`$

解図式の図式の形状：

$`\quad \xymatrix@C+1pc{
{\bullet} \ar@{~>}[dr] \ar@{_{(}->}[dd]
\ar@{}@/^1.5pc/[dd]|{\text{comm.}}
&{}
\\
{}
&{\diamond}
\\
{\bullet} \ar@{~>}[ur]
&{}
}
`$

頂点と辺の視覚的な修飾は、属性付きグラフの属性として表現可能です。問題図式〈コラージュ図式テンプレート〉やその解図式の形状も属性付き2次元グラフです。冒頭に述べたメタ循環的状況が生じています。

スノーグローブ現象

形状・図式・テンプレートという概念を定義するために、定義のための道具として形状・図式・テンプレートを使っています。結局、「形状・図式・テンプレートが何であるかを知るには、事前に形状・図式・テンプレートを知っている必要がある」のです。オイッ！

このような事態・現象は、スノーグローブ現象とかマイクロコスモ原理とか呼ばれます。「マイクロコスモ原理の恐怖」から引用します。

スノーグローブ現象（snowglobe phenomenon）とは、世界（あるいは環境）の構造が、世界のなかのモノに写し込まれる現象です。特定のモノが持つ構造が世界の構造を反映することになります。

マイクロコスモ原理〈Microcosm principle〉：特定の代数構造は、その代数構造を圏化した構造を備える圏のなかで定義可能である。
もし、マイクロコスモ原理が本当なら、あるモノが棲む世界はそのモノと同種だがより複雑な構造を持ち、その世界が棲むメタ世界はもっと複雑な構造を持ち …… と、悲観的無限後退を余儀なくされる気がします。

以下の過去記事でもスノーグローブ現象／マイクロコスモ原理に言及しています。

このテの話で毎回参照している絵を今回も再掲します。スノーグローブ現象／マイクロコスモ原理の雰囲気は感じ取れるでしょう。上記二番目の過去記事に絵の説明があります。

メタな図式の正確な定義

形状・図式・テンプレートという概念を説明するために使ったメタレベルの形状・図式・テンプレートを、できるだけ正確に定義しましょう。

メタレベルの形状・図式・テンプレートは、メタレベルに居るという以外は、通常の形状・図式・テンプレートと変わりません。つまり、属性付き2次元グラフにより記述できます。属性付き2次元グラフの説明は前回の記事にあります。

属性付き2次元グラフ：図式言語の基本

2次元グラフのセルに付与する属性として、sort属性、kind属性、class属性を考えます。

sort属性の値：

値	意味	制約
obj	値は対象	頂点だけに付けられる、省略可能
mor	値は射	辺だけに付けられる、省略可能
diag	値は図式	辺だけに付けられる
comm	値は可換性（等式）	多角形だけに付けられる

sort属性は、セルの値（val属性の属性値）を、特定の種別のモノに制限します。ここに、diag という値が出てきているのが意味的には循環論法です。が、意味は考えずに、diag という値があるんだ、と了解すれば問題は生じません。

kind属性の値：

値	意味	制約
shape	形状圏内の対象・射・2-射
target	ドクトリン	頂点だけに付けられる

グラフ全体の制約として、kind属性の値が target である頂点はただ1つに限られます。その1つの頂点以外には、$`\T{kind}=\mrm{target}`$ 属性を付けることは出来ません。

class属性の値：

値	意味	制約
incl	形状のあいだの包含射	辺だけに付けられる
retr	包含射に対するレトラクション	辺だけに付けられる

class属性は、辺〈矢印〉が特別な射クラス〈class of morphisms | 射のクラス〉（「射のクラスと制約付きスパン // 圏の射のクラス」参照）に入ることを要求します。

包含射については「包含的圏の事例と反例」、レトラクションについては「射影、入射、セクション、レトラクション」を参照してください。

以上のような属性を使って、先に出た2つの図式の形状を描いてみます。

問題図式の図式の形状：

$`\quad \xymatrix@C+1pc{
{[\T{kind}=\mrm{shape}]}
\ar[dr]^{[\T{sort}=\mrm{diag}]}
\ar[dd]_{[\T{kind}=\mrm{shape}, \T{class} = \mrm{incl}]}
&{}
\\
{}
&{[\T{kind}=\mrm{target}]}
\\
{[\T{kind}=\mrm{shape}] }
&{}
}
`$

解図式の図式の形状：

$`\quad \xymatrix@C+1pc{
{[\T{kind}=\mrm{shape}]}
\ar[dr]^{[\T{sort}=\mrm{diag}]}
\ar[dd]_{[\T{kind}=\mrm{shape}, \T{class} = \mrm{incl}]}
\ar@{}@/^2.5pc/[dd]|{[\T{sort} = \mrm{comm}]}
&{}
\\
{}
&{[\T{kind}=\mrm{target}]}
\\
{[\T{kind}=\mrm{shape}] }
\ar[ur]_{[\T{sort}=\mrm{diag}]}
&{}
}
`$

視覚的な修飾の約束

形状である属性付き2-グラフを描くときの約束をします。

$`\T{kind} = \mrm{shape}`$ である頂点は黒丸 $`\bullet`$ で描く。
$`\T{kind} = \mrm{target}`$ である頂点はダイヤモンド形 $`\diamond`$ で描く。
$`\T{sort} = \mrm{diag}`$ である辺はグニグニした矢印 $`\leadsto`$ で描く。
$`\T{class} = \mrm{incl}`$ である辺は包含っぽい矢印 $`\incto`$ で描く。
$`\T{class} = \mrm{retr}`$ である辺は矢頭が二重の矢印 $`\fibto`$ で描く。
$`\T{sort} = \mrm{comm}`$ である多角形は内部に $`\T{comm.}`$ と書き込む。

前節の2つの属性付き2-グラフは次のように描けます。

$`\quad \xymatrix@C+1pc{
{\bullet}
\ar@{~>}[dr]
\ar@{_{(}->}[dd]
&{}
\\
{}
&{\diamond}
\\
{\bullet}
&{}
}
`$

$`\quad \xymatrix@C+1pc{
{\bullet}
\ar@{~>}[dr]
\ar@{_{(}->}[dd]
\ar@{}@/^1.5pc/[dd]|{\T{comm.}}
&{}
\\
{}
&{\diamond}
\\
{\bullet}
\ar@{~>}[ur]
&{}
}
`$

これらは先に示した形状の図を再現しています。

参考までに、別な形状で '$`\fibto`$' を含むものを描いておきます。

$`\quad \xymatrix@C+1pc{
{\bullet}
\ar@{~>}[dr]
\ar@{_{(}->}[dd]
\ar@{}@/^1.5pc/[dd]|{\T{comm.}}
&{}
\\
{}
&{\diamond}
\\
{\bullet} \ar@{_{(}->}[dd]
\ar@{~>}[ur]
&{}
\\
{}
&{}
\\
{\bullet} \ar@{->>}@/_1pc/[uu]
&{}
}
`$