このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

圏論番外：米田の補題の周辺から

雑記／備忘

圏Cの対象AとBが同型であることを示すには、f:A→B、g:B→A、f;g = idA、g;f = idB であるfとgを、C内で探す／構成することになります。場合によっては、条件を満たすfとgを直接的に見いだすより、あるメタ定理を使った方が簡単になることもあります。そのメタ定理とは：

  • どんな対象Xに対してもC(X, A)とC(X, B)が同型であり、それらの同型が自然なら、AとBは同型である。

“同型達が自然”とは、各成分がすべて同型である自然変換が存在することなので、その自然変換をτ＜タウ＞とすると、次のように言えます。

  • 自然変換τ:C(-, A) ⇒ C(-, B) が存在し、τが可逆（成分ごとに可逆）なら、AとBは同型である。

この事実は、米田の補題から出てくるのですが、ここでは直接的に示してみます。「直接的」とは言っても、米田の補題の証明の一部分を切り取ったような感じなのですが、それでも少しだけ簡明でしょう*1。

以下で、いま述べたこの定理をできるだけ明白・露骨・丁寧に説明したいと思います。最後のほうで、この定理の応用例を挙げます。

（[追記 date="翌日"]'Y'と'X'、'f'と'i'を書き間違えていたところがあったので、修正しました。[/追記]）

内容：

参考：

記号の約束

これから以降、矢印で図示されるものが3種類登場します。

  1. 圏の射 f:X→Y
  2. 関手 F:C→D
  3. 自然変換 α:F→G

多少なりとも混乱を避けるために次の約束をします。

  1. 圏の射は小文字（圏の対象は大文字）
  2. 関手は大文字
  3. 自然変換はギリシャ文字

圏はイタリックで示します。自然変換を表す矢印は「⇒」を使うことにします。

説明のために非形式的なラムダ記法を使います。これは、f(x) = … と書く代わりに f = λx.(…) とも書くというだけのことです。変数としてのハイフン「-」は、無名のラムダ変数だ（λが省略されている）と思ってください*2。

反変ホム関手

ホムセットを関手とみなすと、とても便利な道具になります。ホムセットから作られる関手には、二項ホム関手C(-, -)、単項反変ホム関手C(-, A)、単項共変ホム関手C(A, -)があります。ここでは、単項反変ホム関手について述べます。

圏Cの対象Aを1つ選んで固定します。このAから集合圏Setへの反変関手P:C→Setを定義しましょう*3。反変関手Pは対象Aから決まるので、そのことを明示したいときはPAと書きます。

まず、Cの任意の対象Xに対して P(X) = C(X, A) とします。ホムセットC(X, A)は集合*4なので、まちがいなく集合圏Setの対象です。

Cの射 f:X→Y に対して、P(f):P(Y)→P(X) を定めなくてはなりませんが、それは、

  • u∈P(Y) に対して (P(f))(u) = f;u

とします -- いいですか、この定義を理解できないと先に進めませんよ。下の図を眺めながら、続く説明をヨーク読んでください。

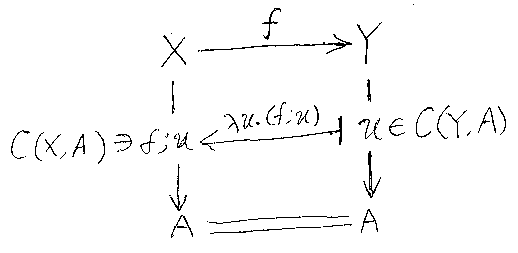
P(Y) = C(Y, A) なので、u∈P(Y) とは、u∈C(Y, A) のことですね。これは、C内で u:Y→A のことです。f:X→Y だったので、C内でfとuをこの順で結合できます。その結合が f;u です。(f;u):X→A ですから (f;u)∈C(X, A) となります。つまり、u∈P(Y) に対して (f;u)∈P(X) なので、λu.(f;u) は P(Y)→P(X) なる関数（集合圏の射）を定義します。λu.(f;u) はfによって決まるので、P(f) = λu.(f;u) と書いたわけね。以下では、(P(f))(u) と書くと括弧が煩雑なので、P(f)(u) と書きます。

以上で定義したPが反変関手であるためには、次の条件を満たさなくてはなりません。

  • P(f;g) = P(g);P(f)
  • P(idX) = idP(X)

P(f;g)(u) を定義に従って計算すれば、(f;g);u。結合律を使えば、(f;g);u = f;(g;u) ですが、右辺は (P(g);P(f))(u)に他なりません。P(idX)(u) も定義により計算して idX;u = u。つまり、P(idX)(u) = u、これは P(idX) が集合P(X)上の恒等（identity）であることを示すので、P(idX) = idP(X) です。

以上のように定義したP = PAを、対象Aによる反変ホム関手（contravariant hom functor）と呼びます。ホムセットを利用して作った反変関手なので、この呼び名となります。

PA(X) = C(A, X)、PA(f)(u) = u;f とすると共変関手が定義できます。こちらは対象Aによる共変ホム関手です。今回は反変ホム関手だけしか使いませんが、共変ホム関手に関してもまったく同様（双対）な議論ができます。

今回示す命題の記述

対象Aによる反変ホム関手をPAと書きましたが、もっと短くA^とも記すことにします。

  • A^(X) = PA(X) = C(X, A)
  • A^(f) = PA(f) = λu.(f;u) （f:X→Y, u:Y→A）

圏Cの2つの対象A, Bに対して、反変関手A^とB^のあいだに自然同型（natural isomorphism）τ＜タウ＞があるとします。つまり、Cの対象Xごとに、集合論的関数τX:A^(X)→B^(X) が割り当てられており、それらはすべて可逆、そして“自然変換の性質”を持つとします。自然変換の性質とは、f:X→Y に対して次の図が可換となることです。

           A^(f)
    A^(Y) ----→ A^(X)
     ｜         ｜
 τ_Y｜         ｜τ_X
     ↓         ↓
    B^(Y) ----→ B^(X)
          B^(f)

この状況のもとで、「対象AとBは、Cのなかで同型である」というのが今回示すべきことです。言葉を換えて言えば、「2つの対象が定義する反変ホム関手が、関手として自然同型（naturally isomorphic）なら、もとの2つの対象が同型だ」ということです。

証明の筋道

AとBが同型であることを示すには、i:A→B, j:B→A, i;j = idA, j;i = idB である射i, jを構成する必要があります。そのようなi, jを、与えられた自然同型τ:A^⇒B^ から絞り出すのです。

実際のi, jの定義はちょっとトリッキーで、「どこから出てきたのか？」がハッキリしません。最初の発見者達は、いくつかの状況証拠から推察したのでしょうが、僕にはうまい説明が思いつきません。i, jを天下りに導入するのをお許しくださいませ。

iとjが定義されてしまえば、i;j = idA, j;i = idB の確認は計算問題です。この計算は良い練習ですので、是非にフォローしてみてください。

iとjの定義

τ:A^⇒B^は自然変換なので、各対象Xごとに集合圏の射τX:A^(X)→B^(X)が在ります。特に、X = A と置けば、τA:A^(A)→B^(A) が得られます。A^(A)はC(A, A)でした。このホムセットC(A, A)には特別な射idAが含まれています。そこで、i = τA(idA) と定義します。i∈C(A, B) なので、圏C内では i:A→B となります。

以上の状況を図に表すと次のようになります。

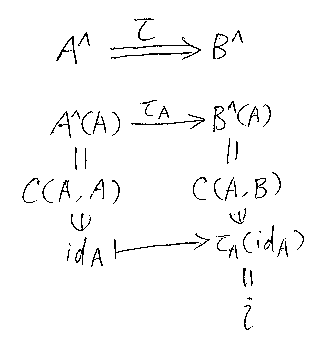
さて、j:B→A は、j = (τB)-1(idB) と定義します。iと同様に図示すれば以下のとおり。τが自然同型（可逆）という前提があるので、jが定義可能となっていることに注意してください。

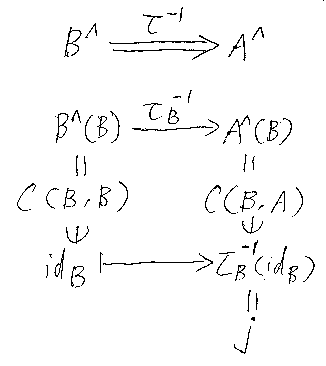
i;j = idA の計算

圏C内では、i:A→B だったので、射iに反変関手A^、B^を作用させると、A^(i):A^(B)→A^(A) と B^(i):B^(B)→B^(A) が得られます。τが A^⇒B^ の自然変換であることから次の図は可換になります。

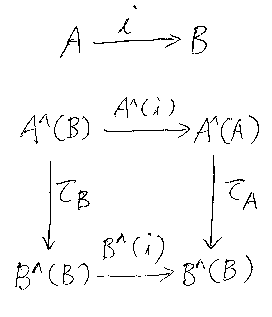
可換性を書き下してみると、

  • A^(i);τA = τB;B^(i) （Set内の等式）

A^(B) = C(B, A) のなかには、先に定義したjが含まれます（j:B→A だったことを思い出してください）。上記の関数等式に、特にjを渡すと、

  • (A^(i);τA)(j) = (τB;B^(i))(j)

等式の左右を別々に計算してみましょう。

   左辺
 = (A^(i);τA)(j)
 // 関数の適用と結合を展開
 = τA(A^(i)(j))
 // A^(i)の定義
 = τA(i;j)

   右辺
 = (τB;B^(i))(j)
 // 関数の適用と結合を展開
 = B^(i)(τB(j))
 // B^(i)の定義
 = i;τB(j)

よって、

  • τA(i;j) = i;τB(j)

この等式の両辺にτA-1を作用させると、

  • τA-1(τA(i;j)) = τA-1(i;τB(j))

ここでまた、等式の左右を別々に計算して、

   左辺
 = τA-1(τA(i;j))
 // τA-1とτAの結合をキャンセル
 = i;j

   右辺
 = τA-1(i;τB(j))
 // iとjを定義に従い展開
 = τA-1(τA(idA);τB(τB-1(idB)))
 // τBとτB-1の結合をキャンセル
 = τA-1(τA(idA);idB)
 // idBは恒等（単位）だから
 = τA-1(τA(idA))
 // τA-1とτAの結合をキャンセル
 = idA

よって、

  • i;j = idA

iとjの役割を入れ替えて計算すれば、

  • j;i = idB

が出ます。

応用例：指数法則

いま示した定理の応用として、デカルト閉圏C内ので指数法則 CA×B ≒ (CA)B （≒は同型）を考えてみます。これを示す際に、C(X, CA×B) ≒ C(X, (CA)B) を示すほうが（少なくとも気分的には）楽でしょう。

随伴性から、左辺C(X, CA×B)はC(X×(A×B), C)と自然同型。同じく随伴性から右辺C(X, (CA)B)はC((X×B)×A, C)と自然同型。さらにC(X×(A×B), C)とC((X×B)×A, C)は、直積の結合性と可換性から自然同型になります。よって、C(X, CA×B) ≒ C(X, (CA)B) の自然同型が言えて、CA×B ≒ (CA)B が帰結します*5。

応用例：表現可能関手の表現対象

反変関手F:C→Setが表現可能（representable）だとは、適当な対象Aがあって、Fと反変ホム関手PA = C(-, A)が自然同型なことです。このとき、反変関手Fは対象Aで表現されるとも言います。そして、Aは反変関手Fの表現対象と呼びます。

例えば、反変ベキ関手Pow*:Set→Set（上付きの星は反変を表す目印）は表現可能で、その表現対象は真偽値の集合{true, false}です。つまり、Pow*(X) ≒ Set(X, {true, false})。

さて、反変関手に対してその表現対象は一意的か？ が問題になりますが、先の定理から「表現可能関手の表現対象が複数在っても互いに同型」であることがわかります。同型の違いを無視すれば（up-to-isoで）表現対象は一意的ですね。

*1:手間は大差ない気がしますが、限定的状況を扱っている分だけ理解しやすいと思います。

*2:圏論では、ハイフン、アンダスコア、アスタリスクなどを無名のラムダ変数に使う習慣があります。

*3:文字Pを選んだのは、単項（共変または反変の1引数）ホム関手を主表現（principal representation）と呼んでいた時代もあったからです。僕には主表現という言葉のほうが馴染みがあります。「米田の補題に向けてのオシャベリ」では主表現という用語を使っています。

*4:圏は常に局所小（locally small）だと仮定してます。局所小の条件を満たさない構造は通常は圏とは呼ばず、疑圏（quasi-category）とか呼ぶようです。

*5:2つの対象の同型を示す場合に、具体的な同型射が未知のままに何か超越的に同型であることだけが帰結するわけではありません。同型射は実際に構成可能です。