(前のエントリーの続きです。)
- 面積 = 内部点の個数 + 周囲の長さに依存する数
の「周囲の長さに依存する数」の予測はつきましたか?
…
…
…
これは、「周囲の長さ/2 - 1」となります。結局、面積を求める公式は、
- 面積 = 内部点の個数 + 周囲の長さ/2 - 1
中藤小学校の先生が出した宿題の場合、周囲の長さが16だったので、「周囲の長さ/2 - 1」の部分が「16/2 - 1 = 8 - 1 = 7」となり、
- 面積 = 内部点の個数 + 7
だったわけです。
下の図は、僕が方眼紙に描いてみた少し複雑な例です。確かに、「面積 = 内部点の個数 + 周囲の長さ/2 - 1」となっていますよ。
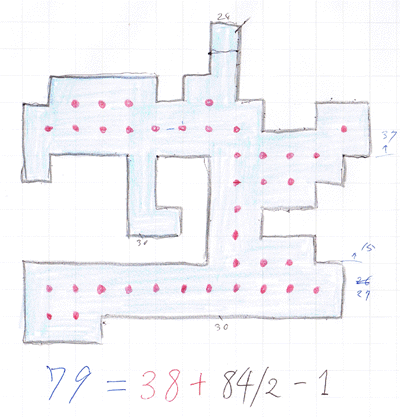
特に、宿題の例(e)のように、内部点をもたない“細い図形”のときは、
- 面積 = 周囲の長さ/2 - 1
となり、面積は周囲の長さだけで決まる(そして逆に、周囲の長さは面積だけで決まる)ことになります。例えば次の2つの図形は、形は違いますが、同じ面積と同じ周囲の長さを持ちます。
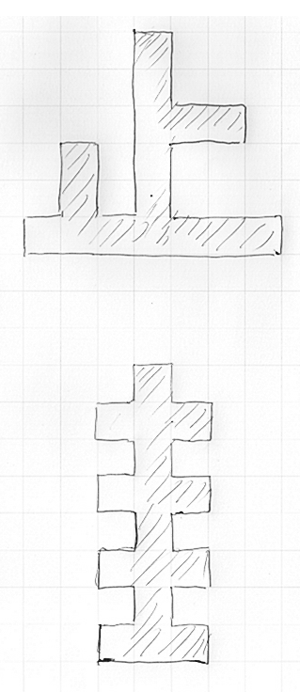
これで話が終わり? いえいえ、これからが本題です。平面に正方形のタイルを並べてできる図形に関して、面積公式をできるかぎり一般化しましょう。予備知識は何も要らないし、計算は加減乗除だけです。じっくり/ゆっくり/しっかり考えることができるなら、小学校高学年くらいから理解可能な話です。高校生くらいまでのお子さんと一緒に考えてみる題材にうってつけでしょう。でも、考えるスタミナが不足していると、大学生でも大人でも挫折するかも。
まず、大前提として、タイルは方眼紙の升目に合わせて置くことにします。次のようなズレた置き方はダメです。
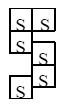
実は、「面積 = 内部点の個数 + 周囲の長さ/2 - 1」という公式は、単純な領域に対してしか成立しません。複数の“島”からなる領域や穴があいた(島に“湖”がある)領域では破綻<はたん>します。次の例で確かめてみてください。(Sと書いてないところはタイルがありません。)
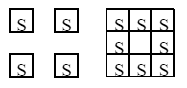
複数の島と湖を許す領域には対しても適用できる公式は、
- 面積 = 内部点の個数 + 周囲の長さ/2 - オイラー数
となります。オイラー数に関しては後で説明します。
さらに、下図のように、2個のタイルが1点で接触することを許すと、上の公式も成立しなくなります。
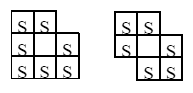
2個のタイルが接触する点を(ちょっと大げさですが)“特異点”と呼ぶとして、特異点がある場合まで面積公式を一般化することができます。
これらの公式と関連する概念を納得したいかたは、さらに続きを読んでみてください。
最初の記事「福井市の小学生が驚くべき発見」の冒頭で書いた「たまたま目にした論文」とは、
- Tetsunori KUROGI, Osami YASUKURA: FROM HOMMA'S THEOREM TO PICK'S THEOREM, Osaka J. Math. 42 (2005), 723-735 (http://projecteuclid.org/DPubS/Repository/1.0/Disseminate?view=body&id=pdf_1&handle=euclid.ojm/1153494548)
です。僕の一連の記事(シリーズ)では、上記論文と少し違う方法で面積公式を導く予定です。