カルタン微分計算系はいいぞ

昨日と一昨日話題にしたカルタン微分計算系〈Cartan calculus〉ですが、これはとても良いですね。知名度と人気はあまりないらしく、まとまった資料もないのですが、多様体上の微分計算を整理する枠組みとしてすごく便利です。

3つのオペレータ d, L, i に関する6つの等式（うち5つ4つは交換子で書ける）にまとめられているのが素晴らしい。

1. 
2. 
3. 
4. 
5. 
6. 

[追記 date="2022-01-12"]幾何学徒さんのコメントにより、3番目のマジック公式をブラケットからブレイスに訂正しました。ブレイスは交換した積の足し算です。[/追記]

それぞれの公式が、どのオペレータ達を関係付けているかを表にまとめると：

	d	L	i
d	公式 1	公式 2, 公式 3	公式 3
L	-	公式 4	公式 3, 公式 5
i	-	-	公式 6

“公式3＝マジック公式”は、3つのオペレータのあいだの関係を示しています。

公式を番号で識別するのは辛いので、名前を付けておきましょう。

1. 外微分の平方零性〈nilquadraticy | square-zero property〉
2. 外微分とリー微分の交換可能性
3. カルタンのマジック公式
4. リー微分のリー準同型性（X L_X がリー代数の準同型になっていること）
5. リー微分と内微分の交換関係
6. 内微分の交代性〈反対称性〉（i_Xi_Y の X, Y を入れ替えると符号が変わること）

d, L, i はどれも、階付きベクトル空間〈graded vector space〉Ωの自己準同型写像です。オペレータの次数も付けて書けば：

1. d^k:Ω^k→Ω^k+1 （1次のオペレータ）
2. L^k:Ω^k→Ω^k （0次のオペレータ）
3. i^k:Ω^k→Ω^k-1 （-1次のオペレータ）

リー微分Lの0階部分 L⁰:Ω⁰→Ω⁰ は、Dとか∂とも書かれ、L⁰_X は、D_X, ∂_X あるいは単に X とも書かれます。このリー微分の0階部分が偏微分〈方向微分〉と呼ばれる微分演算になります。偏微分を別扱いしてもいい（そのほうが分かりやすい気もする）ですが、リー微分の一部に吸収したほうがスッキリします。

カルタン微分計算系の3つのオペレータと6つの等式をキチンと記述するには、その下部構造や周辺構造を考える必要があります。6つの等式以外に、ライプニッツ律〈ライプニッツの法則〉、ヤコビ律〈ヤコビの恒等式〉、シュバレー／アイレンベルク微分（の定義）、Ωのグラスマン代数構造なども考慮する必要があります。カルタン微分計算系は、それら、関連する諸々の事柄を整理してまとめ上げるテンプレート〈様式 | 書式〉を提供します。

通常の微分計算を、カルタン微分計算系をテンプレートにして整理できれば、微分計算の拡張や変形を考えることもできるでしょう。

---

[追記 date="当日"]
3つのオペレータ d, L, i と6つの公式との関係を絵に描きました。

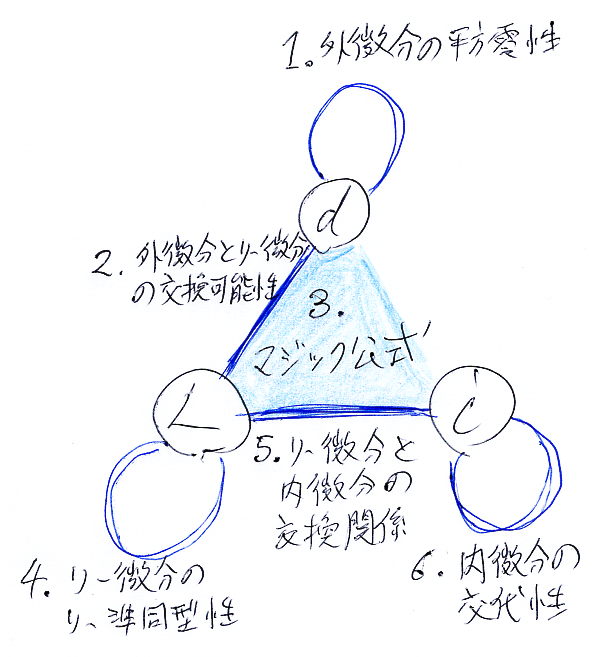
[/追記]